基于改進RRT*算法的機器人路徑規劃

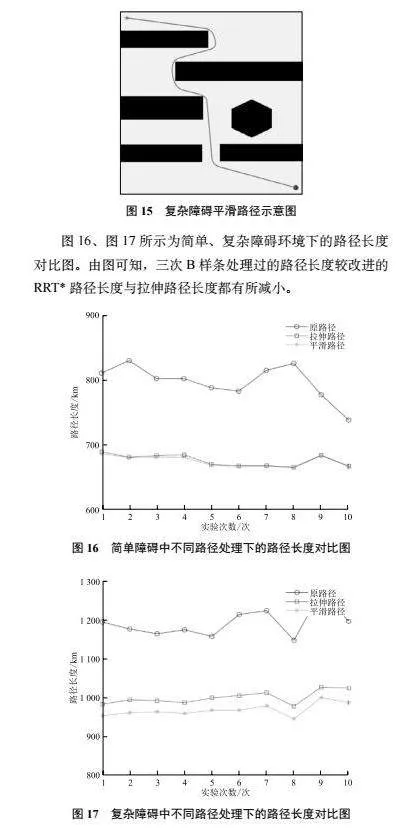
摘 要:針對機器人路徑規劃問題,設計了一種基于改進RRT*算法的機器人路徑規劃方法。首先,針對RRT*算法環境適應能力差的問題,提出基于獎勵的自適應步長設計,以提高RRT*算法的環境適應性;其次,針對RRT*算法在采樣空間隨機采樣的特性,提出偏向目標采樣與貪心采樣結合的采樣策略,并設置路徑長度閾值,對采樣點進行控制;最后,針對路徑冗余且存在尖角的問題,采用先對路徑進行拉伸處理再進行平滑處理的方式來解決。實驗結果表明,所提出的改進RRT*方法相較于其他方法,效率更高、運行時間更短,在路徑的平滑處理方面表現出色。
關鍵詞:改進RRT*;自適應步長;偏向目標采樣;路徑拉伸;路徑平滑;路徑規劃
中圖分類號:TP242 文獻標識碼:A 文章編號:2095-1302(2025)05-00-06
0 引 言
路徑規劃問題可以描述為以一定評價指標(如路徑長度最短、路徑拐點最少)為目標,根據給定的地圖或網絡,找到從起點到終點且不發生碰撞的最優路徑[1]。路徑規劃是機器人移動的基礎,是實現機器人自主導航和任務執行的關鍵技術之一。現階段路徑規劃方法主要分為圖搜索方法(如A*算法)、基于模型的方法(如動態規劃法)、機器學習方法[2](如人工神經網絡)以及基于采樣的路徑規劃方法(如快速搜索樹算法)。圖搜索方法能夠找到全局最優解,但其在面對大規模環境時計算復雜度較高。基于模型的方法可以考慮機器人的運動特性,但對環境模型的準確性要求較高。機器學習方法的環境適應性較強,但需要大量的訓練數據及計算資源,同時易陷入局部最優。基于采樣的路徑規劃方法,在計算效率方面更具優勢。快速搜索樹(Rapidly-exploring Random Trees, RRT)算法是基于采樣的路徑規劃方法之一[3]。RRT算法通過隨機采樣及快速擴展在搜索空間構建一棵樹,完成對搜索空間的探索并找到可行路徑,適用于各種復雜環境和高維空間的路徑規劃,但其生成的路徑不一定是最優路徑。針對這一問題,文獻[4]提出了RRT*算法,用于獲得全局最優路徑,但RRT*算法的運行時間較長。為了解決這一問題,文獻[5]提出了RRT-Connect算法,該算法采用雙向搜索策略來提高算法的運行效率;文獻[6]提出了改進的RRT*與動態窗口法(Dynamic Window Approach, DWA)相融合的動態路徑規劃方法,以實現移動機器人在復雜動態障礙物環境中的避障;文獻[7]提出了MI-RRT*算法,該算法引入貪心采樣和自適應步長的方法來提高算法收斂速度,降低內存占用;文獻[8]提出了黃金正弦下的RRT*勢場算法,利用人工勢場對全局路徑進行預處理,再利用黃金正弦進行局部路徑尋優,實現了三維環境下的路徑規劃。
針對RRT*算法對環境變化適應性差的問題,本文建立了步長調整與環境變化的隨動關系,提出了一種改進的RRT*算法。該算法基于獎勵機制根據環境變化自適應調整步長,通過在迭代過程中不斷對RRT*擴展步長進行調整,實現對當前周邊環境的適應。針對RRT*算法采樣目的性不強的問題,提出偏向目標采樣與貪心采樣相結合的采樣策略,同時引入路徑長度閾值,以提高RRT*算法采樣的目的性。針對RRT*算法規劃的路徑冗余點多、尖角多的問題,采用先對路徑進行拉伸處理再進行平滑處理的方式來解決。
1 RRT*算法介紹
RRT算法以起始點為根節點,以步長為增量,構建搜索樹,通過反向查找形成可行路徑。假設機器人的起始位置為gbegin,結束位置為gend,RRT算法單步擴展如圖1所示。
RRT算法在采樣空間內隨機確定采樣點grand,遍歷隨機樹葉子節點集合,找到與隨機采樣點grand距離最近的葉子節點gnear,從葉子節點gnear出發沿gnear與grand方向進行一個步長為λ的擴展,得到新節點gnew[9]。若此過程中未碰撞障礙物,則將新節點gnew加入隨機樹,反之則放棄該節點,重新進行擴展,重復以上步驟,直到新節點gnew與結束位置gend距離小于步長λ,代表搜索完成。搜索完成后,從結束位置gend出發,不斷尋找其父節點,直至到達起始位置gbegin,形成路徑。
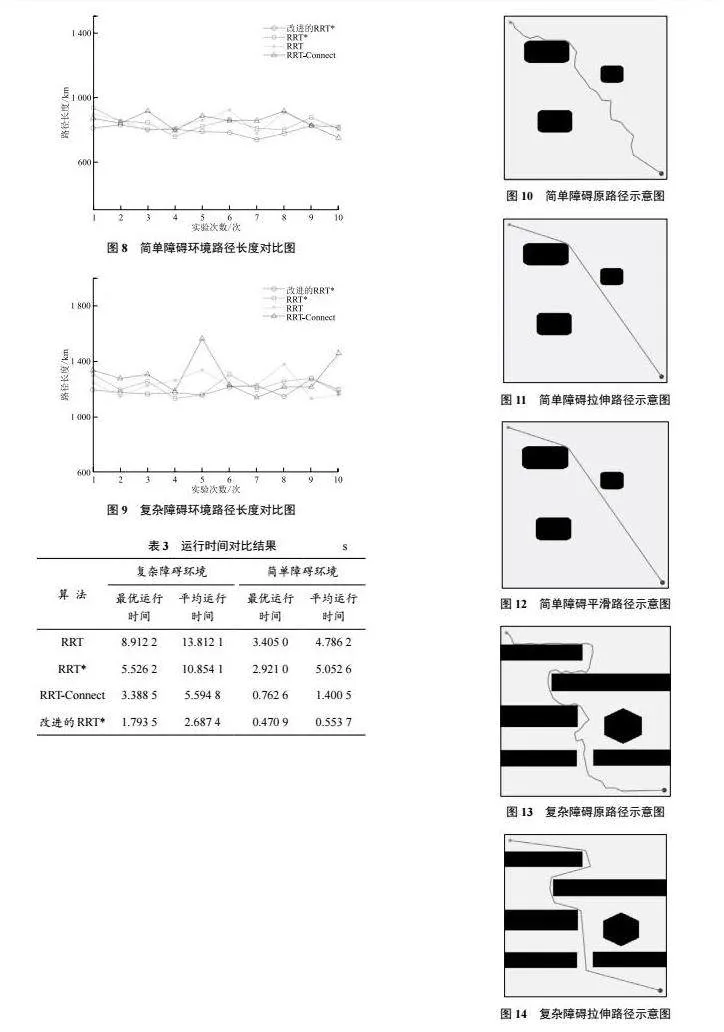
RRT*算法是RRT算法的改進版本,RRT*在RRT算法的基礎上添加了重新選擇父節點與重布線操作。圖2所示為RRT*算法的單步擴展圖,以圖2為基礎對重新選擇父節點與重布線進行介紹。
重新選擇父節點:確定以新節點gnew為圓心,以r為半徑范圍內的葉子節點集合,依次計算從起始位置gbegin經葉子節點集合中的節點至新節點gnew的路徑長度,選擇路徑長度最短的葉子節點作為新節點gnew的父節點。重布線:將新節點gnew與原父節點gnear的連線斷開, 將新節點gnew與新父節點連線。
2 環境建模
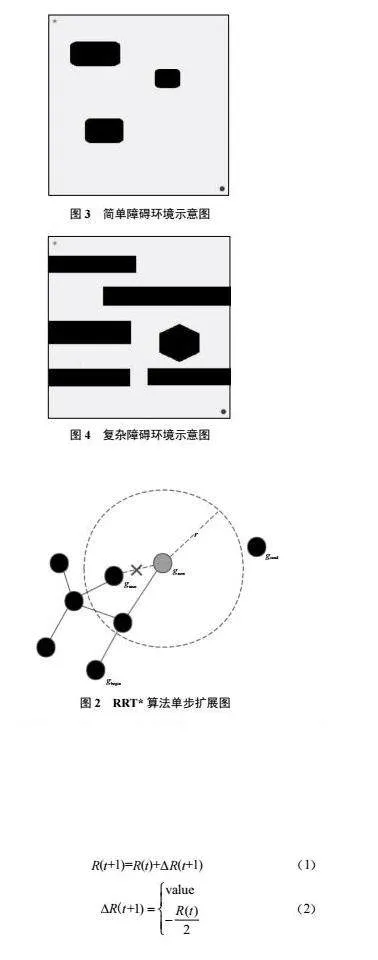
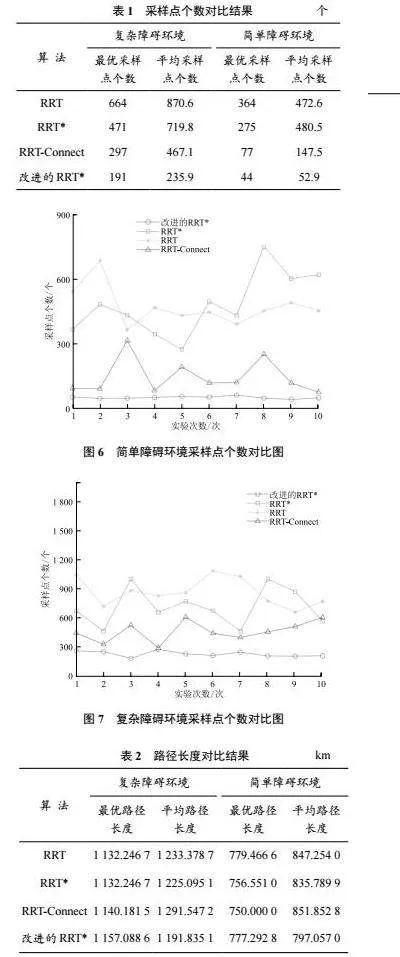
本文采用二維柵格地圖法(Grip Map)[10]進行環境建模。柵格地圖以二維坐標系為基礎,將環境劃分為許多離散的小柵格,每個小柵格的位置對應二維坐標系中的一個坐標點。小柵格中存儲描述環境信息的方法,一般為存儲“1”或“0”。“1”表示該位置存在障礙,不能通行;“0”表示該位置無障礙,可以通行。設置兩種路徑規劃環境,一種是簡單障礙環境;第二種是復雜障礙環境,柵格大小為500×500,起始節點坐標為(20,480),結束節點坐標為(480,20),二維柵格地圖法環境建模結果如圖3、圖4所示。
3 改進的RRT*算法
3.1 基于獎勵的自適應步長
3.1.1 步長分析
RRT*算法確定當前目標位置后,計算所有葉子節點與采樣點位置的距離,取最近的葉子節點沿采樣節點位置方向行進步長λ。由此可見,步長是RRT*算法中的一個重要參數,它決定了樹中節點與節點間的距離。
步長對RRT*算法的影響主要體現在以下兩個方面:
(1)路徑質量:步長越小,算法搜索的路徑精度越高。較小的步長可以使得RRT*算法更加細致地搜索空間,并找到更優的路徑。然而,因為需要生成更多的節點,較小的步長也會導致算法的運行時間增加。
(2)算法效率:步長越大,算法搜索的速度越快。較大的步長可以使得RRT*算法在搜索空間中快速生成節點,從而加快算法的運行速度。然而,因為可能會錯過更優的路徑,較大的步長也可能導致算法搜索的路徑質量下降。
3.1.2 基于獎勵的自適應步長設計
步長直接決定RRT*算法的搜索效率及質量。本文受強化學習獎勵函數[11]啟發,提出基于獎勵的自適應步長設計。
(1)獎勵函數
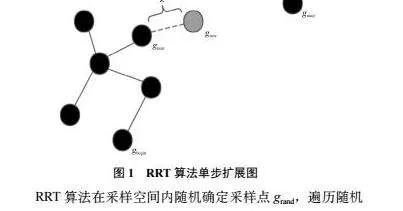
在強化學習中智能體的每一步狀態會返回一個特殊信號,稱為獎勵R。假設智能體當前狀態為S(t),當前獎勵為R(t),若此時智能體未碰撞障礙物,則傳遞獎勵,反之則傳遞懲罰。獎勵函數如式(1)、式(2)所示:
(2)慣性因子
慣性是指物體保持原運動狀態的能力。基于獎勵的可變步長設計,步長跟隨獎勵的變化而變化。若智能體連續多次未觸及障礙區域,則會造成獎勵增長過快,導致步長增長過快。同時,步長越長,智能體觸及障礙區域的概率越大。故若出現此種情況,則會造成連續懲罰,導致步長大量回撤,影響程序運行速度。故本文引入慣性因子θ對步長進行控制。文獻[12]與文獻[13]對慣性因子的設置問題進行了探討,發現慣性因子設置動態的值比設置固定的值取得的效果更加優秀,故本文慣性因子采用線性遞減策略,見式(3)、式(4):
3.2 采樣策略
由于RRT*算法采取隨機采樣策略,路徑的質量又取決于隨機采樣的分布,所以在某些情況下,RRT*算法可能生成一條較長的路徑。針對這一問題,本文的采樣策略首先執行貪心采樣。貪心采樣策略通過設置貪心采樣閾值p, p∈[0, 1],在進行采樣時會生成一個隨機值k, k∈[0, 1],若k小于p,則直接將結束位置gend作為采樣點,否則按照偏向目標采樣進行采樣。偏向目標采樣[14]首先從地圖中隨機確定臨時采樣點ggoal,然后將臨時采樣點與結束節點gend進行連線,在連接線上采用均勻方式隨機確定采樣點ggoal并確定新節點gnew,同時設置路徑長度閾值Dmax,計算從起始位置經新節點到結束位置的路徑長度。若路徑長度大于路徑長度閾值,則重新進行采樣,反之,則執行RRT*算法的其他步驟。從起始位置經新節點到結束位置的路徑長度計算公式如下:
4 路徑拉伸與平滑
4.1 路徑拉伸
路徑拉伸處理在RRT*算法已生成的路徑節點集合基礎上進行。主要思想是根據路徑的兩個端點判斷從節點g1直接到達節點g3中間是否存在障礙物,若不存在則直接忽略兩個端點中間的其他路徑節點,如圖5所示。
4.2 路徑平滑
對路徑進行拉伸處理后,雖然刪除了路徑上的冗余節點,但是路徑仍然存在尖角,不利于車輛轉向。針對這一問題,采取三次B樣條曲線[15]對路徑進行平滑處理。設有控制頂點p0, p1, p2, ..., pn,則k次B樣條表達式見式(8):
5 仿真實驗分析
為了驗證改進的RRT*算法在簡單障礙環境與復雜障礙環境下的實用性和可用性,采用傳統的RRT算法、RRT*算法、RRT-Connect算法與改進的RRT*算法分別在簡單、復雜障礙環境下進行路徑規劃仿真,試驗次數為10次,旨在驗證改進的RRT*算法的隨機樹生成采樣點的目的性是否更強以及其路徑規劃效果和路徑規劃效率。本文使用MATLAB 2021版本進行實驗。
5.1 采樣點個數對比
從表1中可知:改進的RRT*算法無論在簡單障礙環境下還是復雜障礙環境下,最優采樣點個數與平均采樣點個數均少于其余3種算法。由此分析:改進的RRT*算法的運行效率應優于其他3種算法,這得益于改進的RRT*算法采用目的性更強的采樣策略。
圖6、圖7所示為各算法在簡單、復雜障礙環境下的采樣點個數對比圖。改進的RRT*算法的隨機采樣點個數變化趨勢較其他3種算法較為平緩。這表明了改進的RRT*算法在采樣點的隨機性方面展現出了更強的魯棒性,不會因為較小的變化而導致結果發生顯著變化。
5.2 路徑長度對比
各算法在復雜、簡單障礙環境下的路徑長度對比實驗結果見表2。
由表2可以看出:改進的RRT*算法雖然在路徑規劃的最優解上沒有其他算法優秀,但是在平均路徑長度方面表現出良好的性能;雖然改進的RRT*算法的采樣點數減少,但是搜索質量確有提高。這主要是因為本文采取自適應步長設計,當遇到障礙物密集時,采用小步長進行擴展;當遇到障礙物松散時,采用大步長進行擴展。
圖8、圖9所示為各算法在簡單、復雜障礙環境下的路徑長度對比圖。由圖可知,隨著實驗次數的增加,改進的RRT*算法的路徑長度變化更平緩,表明該算法受其內部隨機性影響較小,具有較好的魯棒性。
5.3 運行效率對比
各算法在復雜、簡單障礙環境下的運行時間對比結果見表3。
由表3可知,改進的RRT*算法相較于其他3種算法在運行效率上有較大提升;在簡單障礙環境下,運行效率提升尤為明顯。在復雜障礙環境下改進的RRT*算法相較于運行速度較快的RRT-Connect算法,速度提升了52%;而在簡單障礙環境下,這一提升更是達到了60%。這主要是因為改進的RRT*算法采樣的目的性更強,面對簡單障礙環境時,改進的RRT*算法的擴展步長更長,使得算法可以更快地到達目標位置。
5.4 路徑平滑對比
6 結 語
本文針對RRT*算法環境適應性差的問題,提出了一種基于獎勵的可變步長策略,該策略可使RRT*算法根據所處的環境動態調整步長,提高環境適應性。針對RRT*算法采樣的隨機性,提出貪心采樣與偏向目標采樣相結合的采樣策略,同時引入路徑長度閾值,提高采樣的目的性、有效性,加快算法的運行效率。針對RRT*算法規劃的路徑存在冗余及尖角的問題,采用先對路徑進行拉伸處理以去除冗余路徑,再用三次B樣條曲線進行平滑處理以去除尖角的策略。雖然本文規劃的路線較短且平滑,取得了良好的效果,但是并沒有實際考慮機器人的運動模型,后續將結合機器人的實際運動模型進行完善。
參考文獻
[1] FRAZZOLI E, DAHLEH M A, FERON E. Real-time motion planning for agile autonomous vehicles [C]// Proceedings of the 2001 American Control Conference. Arlington, VA, USA: IEEE, 2001.
[2]謝文顯,孫文磊,劉國良,等.基于強化學習的機器人智能路徑規劃[J].組合機床與自動化加工技術,2022,581(7):13-17.
[3] LAVALLE S M. Rapidly-exploring random trees: a new tool for path planning [J]. Computer science dept, 1998, 98(11).
[4] KARAMAN S, FRAZZOLL E. Sampling-based algorithms for optimal motion planning [J].The lnternational journal of robotics reseach, 2011, 30(7): 846-894.
[5] KUFFNER J J, LAVALLE S M. RRT-Connect: an efficient approach to single-query path planning [C]// Proceedings of the 2000 IEEE International Conference on Robot and Automation. San Francisco, CA, USA: IEEE, 2000.
[6]張瑞,周麗,劉正洋.融合RRT*與DWA算法的移動機器人動態路徑規劃[J].系統仿真學報,2024,36(4):957-968.
[7]于強,彭昭鴻,黎旦,等.基于MI-RRT*算法的路徑規劃研究[J].現代防御技術,2023,51(4):116-125.
[8]彭熙舜,陸安江,劉嘉豪,等.黃金正弦下RRT*勢場算法的三維路徑規劃研究[J].火力與指揮控制,2022,47(12):145-151.
[9] AN B, KIM J, PARK F C. An adaptive stepsize RRT planning algorithm for open-chain robots [J]. IEEE robotics and automation letters, 2018, 3(1): 312-319.
[10]彭君. 改進RRT算法在移動機器人路徑規劃中的應用研究[D].南京:南京郵電大學,2022.
[11]曹毅, 李磊, 張景濤.基于深度強化學習的機械臂避障路徑規劃研究[J].制造業自動化,2023,45(6):160-164.
[12] SHI Y, EBERHART R C. A modified particle swarm optimizer [C]// Proeeedings of the IEEE International Conference on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 1998: 69-73.
[13] EBERHART R C, SHI Y. Comparing inertia weights and constriction factors in particle swarm optimization [C]// Proceedings of the 2000 Congress on Evolutionary Computation. Piscataway, NJ, USA: IEEE, 2000: 84-88.
[14]趙文龍,ABDOU Y M. 基于改進RRT算法的移動機器人路徑規劃方法[J].計算機與數字工程,2022,50(8):1733-1738.
[15]張宇龍,楊金山, 王鵬偉,等.基于B樣條算法的智能車輛局部避障路徑規劃[J].山東理工大學學報(自然科學版),2023,37(4):36-39.

