全等三角形開放性試題的特點

劉金江

開放性數學問題有利于激發我們的創新意識，啟迪創新思維，培養創新精神，是中考命題的熱點.本文舉例說明全等三角形開放性題的特點.

一、條件開放

給出部分條件和問題結論，要求我們探索該結論成立的條件，因使結論成立的條件往往不惟一，這就是條件開放題.它要求我們從結論出發，逆向、多角度分析問題.

例１如圖１，在△ＡＢＣ中，ＡＤ⊥ＢＣ，ＣＥ⊥ＡＢ，垂足分別為Ｄ、Ｅ，ＡＤ、ＣＥ交于點Ｈ，請你添加一個適當的條件：，使△ＡＥＨ≌△ＣＥＢ.

分析：由題意知，在△ＡＥＨ、△ＣＥＢ中，∠ＥＡＨ＝∠ＥＣＢ，∠ＨＥＡ＝∠ＢＥＣ，只要再加一條對應邊相等的條件即可，因此添加的條件可為ＡＥ＝ＣＥ或ＥＨ＝ＥＢ或ＡＨ＝ＣＢ.

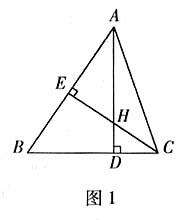
評點：這道題要求我們全面掌握全等三角形的知識，且具有較強的分析能力、推理能力.這類題改變了被動地利用條件解題的思路，要求大家主動獲取條件，進行創造性學習.

二、結論開放

給出條件，要求根據條件探索結論，由于符合條件的結論往往呈現多樣性，這就是結論開放題.這類題要求我們進行大膽合理的猜想，發現規律，得出結論.

例２如圖２，若ＡＣ、ＢＤ、ＥＦ兩兩互相平分于點Ｏ，請寫出圖中的一對全等三角形：.（只需寫一對即可）

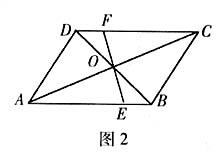
分析：不難發現圖２中有多對全等三角形．如△ＡＤＯ≌△ＣＢＯ，△ＤＯＦ≌△ＢＯＥ，△ＤＯＣ≌△ＢＯＡ，△ＡＤＣ≌△ＣＢＡ，△ＦＯＣ≌△ＥＯＡ.

例3如圖３，Ｄ是ＡＣ上一點，ＢＥ∥ＡＣ，ＢＥ＝ＡＤ，ＡＥ分別交ＢＤ、ＢＣ于點Ｆ、Ｇ，∠１＝∠２.

問圖中哪個三角形與△ＦＡＤ全等？并證明你的結論.

解：△ＦＥＢ≌△ＦＡＤ.

證明：∵ＡＤ∥ＢＥ，

∴∠１＝∠Ｅ.

又∵∠ＥＦＢ＝∠ＡＦＤ，ＢＥ＝ＡＤ，

∴△ＦＥＢ≌△ＦＡＤ.

評點：這類問題讓我們體會到同一條件下可以得到多種結果，能培養思維的靈活性和發散性.解題時要注意題后括號中的附加說明.

三、策略開放

例4此題有Ａ、Ｂ、Ｃ三類題目，其中Ａ類題４分，Ｂ類題６分，Ｃ類題８分，請你任選一類證明，多證明的題目不記分.

（Ａ類）已知：如圖４，ＡＢ＝ＡＣ，ＡＤ＝ＡＥ.求證：∠Ｂ＝∠Ｃ.

（Ｂ類）已知：如圖５，ＣＥ⊥ＡＢ于點Ｅ，ＢＤ⊥ＡＣ于點Ｄ，ＢＤ、ＣＥ交于點Ｏ，且ＡＯ平分∠ＢＡＣ.求證：ＯＢ＝ＯＣ.

（Ｃ類）已知：如圖６，△ＢＤＡ、△ＨＤＣ都是等腰直角三角形，且點Ｄ在ＢＣ上，ＢＨ的延長線與ＡＣ交于點Ｅ，請你在圖中找出一對全等三角形，并寫出證明過程.

證明：（Ａ類）在△ＡＢＤ和△ＡＣＥ中，

ＡＢ＝ＡＣ，∠Ａ＝∠Ａ，ＡＤ＝ＡＥ，

∴△ＡＢＤ≌△ＡＣＥ，即∠Ｂ＝∠Ｃ.

證明：（Ｂ類）∵ＡＯ平分∠ＢＡＣ，ＣＥ⊥ＡＢ，ＢＤ⊥ＡＣ，

∴ＯＥ＝ＯＤ.

在△ＢＯＥ和△ＣＯＤ中，

∵∠ＯＥＢ＝∠ＯＤＣ＝９０°，ＯＥ＝ＯＤ，∠ＢＯＥ＝∠ＣＯＤ，

∴△ＢＯＥ≌△ＣＯＤ，即ＯＢ＝ＯＣ.

解：（Ｃ類）△ＢＤＨ≌△ＡＤＣ.

證明：∵△ＢＤＡ、△ＨＤＣ都是等腰直角三角形，

∴ＢＤ＝ＡＤ，∠ＢＤＨ＝∠ＡＤＣ＝９０°，ＨＤ＝ＣＤ.

∴△ＢＤＨ≌△ＡＤＣ.

評點：這類試題可以滿足不同水平、不同個性同學的需要，這是尊重個性差異，“讓不同學習風格的人在數學上都有平等發展”的一種嘗試和探索.由于需對這些知識點掌握情況進行一次反思后才能作出選擇，促進了我們認知能力的發展.