海洋平臺結構系統彈塑性整體計算的裂紋柱殼新單元

1 引 言

以柱殼為基本構件的結構系統常見于海洋工程等大型復雜結構物中。由于柱殼良好的綜合性能，船舶與海洋工程的各種平臺大多將其作為主體結構。通常此類平臺造價昂貴，平臺上載有各種專用設備并有較多的人員在平臺上工作，因此一旦發生重大安全事故，將可能造成巨大的生命財產損失，甚至導致海洋環境的嚴重污染和社會層面上的連鎖負面反應；另一方面，海洋平臺在服役期間長期處于較為惡劣的環境之中，盡管平臺的安全性設計要求非常高，但歷史事實表明也未能完全避免災難性事故的發生。應該說在安全系數較大的前提下，一般意義上的強度或失穩破壞不易發生，但究其原因，一個重要的問題是未充分考慮無法回避的自身的隱傷或服役期間所產生的損傷、破損等因素的影響。由于各種交變疲勞載荷的長期沖擊，裂紋損傷是各種損傷中最常見且最危險的一種損傷形式。

另一方面，如何從結構系統的角度判斷在裂紋損傷條件下的安全度，正確評估結構系統的殘余壽命，科學地制定保護維修方案，有效進行裂紋控制，是精確評估平臺安全性的一個重要課題。很明顯,只有實現裂紋損傷條件下的結構系統整體分析才能回答上述相關問題，但用現行的傳統方法無法得到滿意的答案。對于“裂紋”也許會首先想到“斷裂力學”；而涉及到結構系統或許會想到“結構力學”，可這兩者的關注點差別很大。“斷裂力學”可處理線性到非線性，以及脆斷到撕裂的問題，但它最終關注的是如何表達裂紋尖端的力學特性，所以,一般而言它著眼于單一孤立構件的“局部”，其方法不能提供與結構系統之間相互影響的關系；而“結構力學”已可對復雜結構系統進行非線性極限分析，但在其“整體”中無法涉及如裂紋這樣的損傷，即對局部的地方出現的裂紋損傷的力學特性如何表現顯得無能為力。通用的三維有限元方法從原理上似乎可以將上述所謂“整體”和“局部”放在一起求解，但因裂紋尖端奇異性特點，僅對單一裂紋構件和裂紋尖端單元網格的密分數據量就已非常可觀，與之相關聯的結構系統的其它構件則因此很難再考慮。非常大的建模工作量和數據量使得對海洋工程平臺這樣復雜的結構系統的求解變得非常困難。由此產生了研究和開發一個具有有限元特點的含裂紋影響的理想化單元的設想。通過一個單元來包含裂紋影響的力學信息，使單元網格劃分最大限度地減少，從而實現對復雜結構系統整體的分析評價。

目前國內外尚不存在這樣一個完善的單元。由于材料科學的發展，高韌性材料被廣泛使用，在外力作用下，裂紋擴展前，其前端附近將出現不能忽略的較大范圍的塑性區域，在結構系統整體分析中如何考慮這一影響也是一個新課題。

YAO等[1]介紹了裂紋損傷結構系統的彈塑性分析方法，但由于不涉及斷裂力學的內容，事實上只是采用了彈塑性結構力學的分析方法，以致因裂紋而引起的剛性降低，內力再分配無法反映。EI-HADDAD等[2]雖然引入了斷裂力學的內容，但因僅局限于線彈性范圍的靜止裂紋，自然塑性影響無法考慮。BRUST等[3]采用的簡便方法，由于其推導基于指數型材料，故難以用于彈塑性增量矩陣法。劉松柏等[4]雖考慮了非靜定單一構件邊界約束的強弱，但忽略了塑性變形與裂紋撕裂的內在聯系，丟失了耦合關系，和文獻[3]的結果一樣只能是單一裂紋構件的一種近似算法。藤久保昌彥等[5]采用了與文獻[2]相似的方法，通過能量釋放率將一個特殊的裂紋單元結合到一般的梁柱單元中，雖從中也可考慮裂紋前端塑性修正，但從理論上講仍應是線彈性小塑性修正解，并且在全塑性條件下與塑性節點理論不協調，需要進行人工干預，不利于完整意義上的計算機處理。

本文研究開發了可用于裂紋損傷結構系統整體計算的新的彈塑性裂紋單元，新的單元為彌補目前已有工作的不足，重點考慮了韌性材料在裂紋前端進入較大范圍塑性時的彈塑性影響。本研究利用了SANDERS[6]周向壁穿裂紋彈塑性解析解，通過增量微分，獲得了節點內力與位移的顯式增量關系，進而建立了彈塑性裂紋增量剛度方程，并將理論結果通過有限元分析方法，形成了一個新的特殊單元，為實現裂紋損傷結構系統的整體分析奠定了理論基礎。

2 分析方法

分析模型為柱殼，其中無因次軸向坐標為z，距原點的軸向距離為zR。設材料為理想彈塑性材料，裂紋損傷為周向壁穿裂紋，裂紋長所對的圓心角為2α，裂紋面保持全自由；載荷為施加橫截面彎矩，載荷作用方向取使裂紋張開的方向，即保持裂紋處于 Ⅰ 型裂紋破壞狀態(圖1、圖2)。

設參量ε的表達式為:

ε2=(h/R)[12(1-μ2)]-1/2

(1)

式中，μ為泊松比；R為柱殼中面半徑;h為板厚。

無因次載荷參數:

(2)

式中，σF為材料的屈服應力;M為作用彎矩。

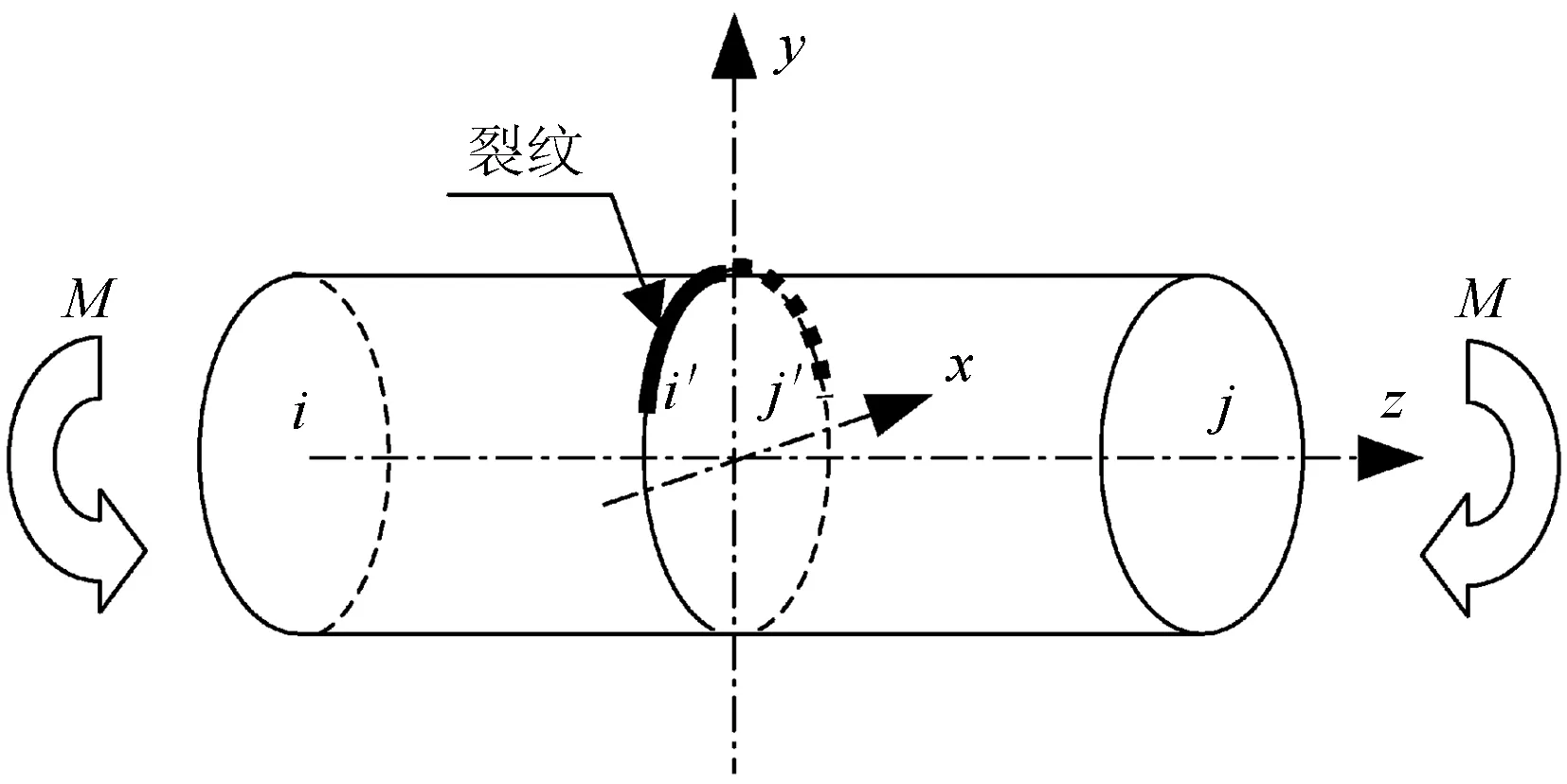
圖1 計算模型

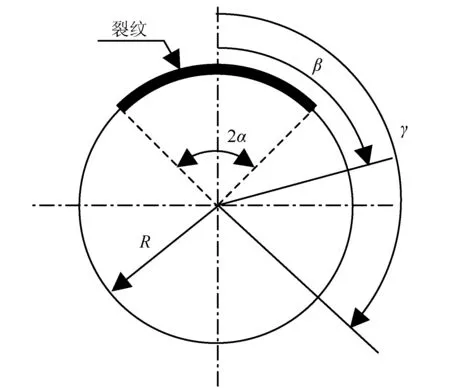
圖2 裂紋截面

2.1 基本理論

由于裂紋的存在，在載荷作用下，裂紋截面附近的截面呈較為復雜的應力分布，實驗和數值仿真結果[7]表明裂紋在柱殼軸向上的影響有限，應力分布從裂紋截面開始沿柱殼軸方向經過大約1/5～1/4柱殼半長的變化，就基本可收斂到相應條件下的非裂紋柱殼的分布狀態，因此從整體上可作為梁考慮，這樣上述發生的變化可認為主要是裂紋截面中性軸位置發生變化所致，裂紋和非裂紋截面在中性軸上的差距，形成一個附加的轉角。另外，在Ⅰ型裂紋彎矩載荷作用下，在截面拉應力區的裂紋前端將出現拉應力Dugdale塑性長度，即圖2中β-α的長度。隨著載荷作用，在截面壓應力區，將可能出現類似的壓應力塑性長度，文獻[6]將此稱為壓應力Dugdale塑性長度，即圖2中的π-γ的長度。SANDERS利用殼理論邊值解和Dugdale裂紋模型推導了裂紋附加轉角理論解，而且結果與軸向z坐標無關，其表達式為：

(3)

式中，Θ為裂紋附加彎曲轉角；d可理解為裂紋對圓柱殼柔度的影響，其表達式如下:

(4)

Csinβ=β-α+sin(β-α)-

(5)

πc=-(β-γ+sinβcosβ-sinγcosγ)C-

(π-γ-sinγcosγ)G1+

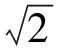
2(sinα-sinβ-sinγ)+(π-γ)+(β-α)cosα+

cosβsin(β-α)-sinγcosγ

(6)

Psinx=Qcosx+β-α-σBsinβ

(7)

Q=-π+γ+σBsinγ

(8)

(9)

(10)

其中，Dugdale拉伸和壓縮塑性長度β和γ，從式(11)的超越方程中求解。

(11)

式中，

N1=[sinβ-sinα+(β-α)cosβ]sinx-

N2=[sinγ-(π-γ)cosγ]sinx+

初始，壓縮塑性區域不出現時，γ=π，并由式(12)的不等式成立[8]，則只需通過式(11)第一式求出β即可，其第二式此時是自動滿足的；當式(12)的不等式不成立時，塑性壓縮長度出現，γ<π。

(12)

2.2 裂紋附加轉角與彎矩的增量關系

式(3)是反映裂紋影響的主要等式，它不僅包含了裂紋存在的影響，而且由前述可知，裂紋截面的大范圍的塑性影響也計入其中，利用該式將可以有效解決本文引言中所提出的問題。由于上述非線性因素，從式(3)～式(11)顯然可知，裂紋附加轉角與彎矩的關系為隱式，故不宜用矩陣形式表達。另一方面，出于本研究的目的，對于非線性方程求解，運用增量理論是必要的。故這里將推導上述相關公式的增量表達形式。對式(3)進行分析，從Dugdale塑性長度和彎矩的因果關系，可以認為β和γ均應是隨σB的變量，可以推導出裂紋附加轉角的增量表達式為:

(13)

經整理可得另一種表達方式:

(14)

由上述對β和γ的考慮，同樣可對式(11)進行微分計算，從而可得如下表達式:

(15)

將式(15)整理得到:

(16)

將式(16)代入式(14)，消去dβ和dγ組成的向量，可得：

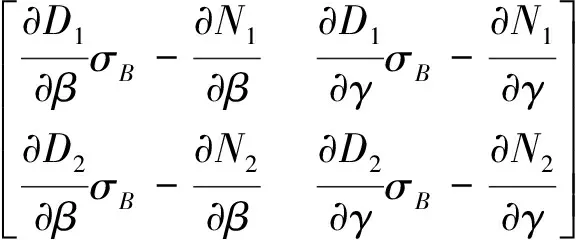
(17)

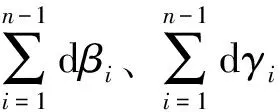
2.3 裂紋單元增量剛度方程

如圖1所示，選擇裂紋左右截面分別為i′,j′兩節點。利用有限元梁柱理論可以將附加轉角與彎矩的關系寫成單元剛度方程式的形式，即

(18)

其中，

對于一般梁柱單元，由于剛度矩陣為常量，故其增量形式僅僅將內力和位移向量改為增量寫法即可。

就海洋平臺結構而言，通常殼長度方向的尺度要遠遠大于殼截面的最大尺度，因此采用梁單元是一個合理的選擇。設如圖1所示裂紋損傷的圓柱殼兩端節點分別為i和j，在運用有限元計算進行單元劃分時，可分為3個單元，第一個單元從柱殼左端到裂紋左截面，為i—i′單元，是一般梁單元；第二個單元從裂紋左截面到裂紋右截面，為i′—j′單元，為本文介紹的彈塑性裂紋單元(注意到該單元與長度無關)；第三個單元從裂紋右截面到柱殼右端,為j′—j單元，也為一般梁單元。

由于上述推導建立在有限元框架體系內，由有限元理論，上述各單元可以進行單元剛度矩陣組裝或與全體構件的單元剛度矩陣組裝，形成結構整體的總體結構剛度矩陣，然后實施有限元計算。顯然，這里包含的是有限元單元族中節點數最少的單元，故形成的未知量也是目前有限元計算中最少的，自然對計算機資源的占用和建模處理等工作量也是最少的，從而使對大型復雜結構系統的整體計算成為可能。

當裂紋截面進入全截面塑性，不難推出有下式成立:

(19)

此時裂紋截面已形成塑性節點。在計算處理上只需將本裂紋單元去掉，然后用塑性節點取而代之，其后將與UEDA等[9]的塑性節點法或YAO的計算[1]構成無縫相接，進一步實施裂紋損傷結構系統的極限分析計算。從理論上講，兩者之間的這一過渡具有一致性，從而回避了由于理論上的不一致所帶來的計算上的人為處理，有利于計算機的高效編程和運算。

3 精度的定性分析

從推導過程看，解的誤差主要來自SANDERS的理論解，而SANDERS理論解的主要誤差來源是殼半膜理論和斷裂力學中的Dugdale模型。

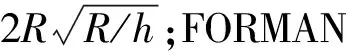
另一方面，來自Dugdale模型的誤差主要是因為塑性判斷使用的是單軸應力條件,并且忽略了塑性區域沿軸向的擴展，因此所獲得的塑性長度常常會偏長，但Dugdale模型巧妙地通過線性結果疊加消除裂紋尖端奇異性的辦法實現了對彈塑性非線性問題的求解，避免了復雜數學推導，目前仍是一種公認的非常有效的方法。其誤差所帶來的結果也是偏于安全的。

在前述整個公式體系中，基本上是對式(3)～式(11)的微分，即是一個正向運算過程，故一般不存在計算上的特別的困難。剩余的計算是增量有限元的常規計算。

4 結 論

本文研究開發了可用于裂紋損傷結構系統整體計算的新的彈塑性裂紋單元，重點考慮了韌性材料在裂紋前端進入較大范圍塑性時的彈塑性影響，形成了一個新的特殊單元，為實現裂紋損傷結構系統的整體分析奠定了理論基礎。獲得了以下結論：

1) 利用SANDERS周向壁穿裂紋彈塑性解析解，通過增量微分運算，獲得了內力與位移的顯式增量關系。

2) 建立了彈塑性裂紋增量剛度方程，形成了節點或未知數最少的彈塑性裂紋單元，依有限元分析方法，該單元可方便地和結構系統中其它有限元單元進行組合裝配并實施整體計算。

3) 定性誤差分析表明對于海洋平臺的主要結構，其誤差為可控。

4) 整個公式體系中，基本上是微分的正向運算，故一般不存在計算上的特別的困難。

5) 該單元的計算可與塑性節點法無縫相接，進行裂紋損傷結構系統的極限分析，實現了兩者在理論上的一致性，回避了在計算上的人為處理，有利于進一步提高計算機的計算效率。

作為下一步的工作，該研究將進一步考慮裂紋擴展的影響、擴充組合載荷條件下的單元并且完成該單元的定量精度校核。

[1] YAO T, MOAN T. Elastic-plastic behavior of structural members and systems with crack damage[J]. J. of Soc. Naval Arch., 1987, 161(6): 274-284.

[2] EI-HADDAD M N, RAMADAN O M, BAZARAA A R. Analysis of frames containing cracks and resting on elastic foundations[J]. Intl. J. Fracture, 1990, 45: 81-102.

[3] BRUST F W, GILLES P. Approximate methods for fracture analysis of tubular members subjected to combined tensile and bending loads[J]. ASME J. of Offshore Mechanics and Artic Eng., 1994, 116(11): 221-227.

[4] 劉松柏，安藤柱.き裂とコンプライアンスを有する不靜定な配管系の塑性崩壞舉動と終局強度[J].日本機械學會論文集(A編)，1996, 62(5): 1164-1171.

[5] 藤久保昌彥，趙 耀，矢尾哲也.亀裂損傷を有する円筒部材の曲げ崩壞解析[J]. 西部造船學會會報，1991, 82(8): 177-189.

[6] SANDERS J L.Dugdale model for circumferential through-cracks in pipes loaded by bending[J]. Intl. J. Fracture, 1987, 34: 71-81.

[7] 趙耀.裂紋損傷圓柱殼承載能力的實驗研究[J].華中理工大學學報，1998, 26(5): 54-57.

[8] SANDERS J L.Tearing of circumferential cracks in pipes loaded by bending[J]. Intl.J.Fracture, 1987, 35: 283-294.

[9] UEDA Y, YAO T. The plastic node method: a new method of plastic analysis[J].Computer Method in Appl. Mech. and Eng., 1982, 34: 1089-1104.

[10] TADA H, PARIS P C, IRWIN G R. The stress analysis of cracks handbook[S]. Del Research Corporation,Hellertown, Pennsylvania, 1985.

[11] SANDERS J L. Circumferential through-cracks in cylindrical shells under tension[J]. J. Applied Mechanics, 1982, 49: 103-107.

[12] FORMAN R G, HICKMAN J C, SHIVAKUMAR V.Stress intensity factor for circumferential through cracks in hollow cylinders subjected to combined tension and bending loads[J].Eng. Fracture Mechanics, 1985, 21: 563-571.