列方程解應用題的幾個技巧
劉秀霞
列方程解應用題在初中數學中既是重點,又是難點,有些學生對于方程中數量之間的相依關系及其變換往往識別不清,遇到一些特殊的應用題,更是無從下手,找不到相等關系.如何尋找相等關系,把問題從雜亂的條件中理出頭緒,使問題得以解決,我認為應注意以下幾個方面的問題.
一、注意弄清和掌握基本數量關系
尋找相等關系,首先要弄清并掌握各類應用題中的基本數量關系,如在行程問題中,基本關系有:距離=速度×時間;在勞力調配問題中,基本數量關系有:原有勞力+調配勞力=現在勞力;在利潤率問題中,基本數量關系有:商品利潤=商品售價-商品進價,商品利潤率=商品利潤÷商品進價,然后依著這些數量之間的相等關系,列出有關的代數式并列出方程.
【例1】 商品對某種商品作調價,按原價的8折出售,此時商品的利潤率是10,此商品的進價為1600元,商品的原價是多少?
分析:本題中依著的數量關系是,商品的利潤率=商品利潤÷商品進價.
解:設商品原價為x元,根據題意可列出的方程為:80x-1600/1600=10%.
二、注意理解關鍵性詞語
有些應用題的數量關系,是通過題目中的一些關鍵性詞語明顯地表示出來,這些關鍵性詞語常見的有:和、差、倍、分、大、小、多、少、相向、相遇、增加、減少、超過、提前等等.它們與列方程有著直接關系,解題時必須理解其確切的含義,然后就可以通過這些詞語尋找相等關系,從而列出方程.
【例2】 某市居民2001年末的儲蓄存款達到7079萬元,比2000年末的儲蓄存款的15倍還多了4萬元,求2000年末的儲蓄存款.
分析:本題中的關鍵性詞語是“……15倍還多……”.
解:設2000年末的儲蓄存款為x元,根據題意可列出的方程為:15x+4=7079
三、注意題目中的不變量
尋找相等關系,也可以從不變量入手,所謂不變量,就是一定的數量關系,在行程問題中,同向追及,則從出發到追及地或距離不變,或時間不變;相向相遇所走的距離和不變;在工程問題中總工作量不變;在勞力調配問題中,總人數不變;在等積變形中,體積不變等等.抓住了這些不變量,也就是找到了相等關系.
【例3】 將內徑為200毫米的圓柱形水桶中的滿桶水倒入一個內部長、寬、高分別為300毫米、300毫末、80毫米的長方形鐵盒,正好倒滿,求圓柱形水桶的高.
分析:本題中的不變量是圓柱體體積=長方體體積.
解:設圓柱形水桶的高為x毫米,列出的方程為:300×300×80=π(200/2)2x.
四、列表思維法
在分析應用題時,列表思維法能清晰地顯現題意,通過列表、填空,由空與空之間的關系去尋找方程,從而為正確地解方程應用題奠定了基礎,這類問題的特點是,設出兩個或三個未知數,根據題意建立起兩個或三個相等關系,從而列出方程組解答實際問題.
【例4】 小華買了10分與20分的郵票共16枚,花了2元5角,問:10分與20分的郵票各買了多少枚?

分析:將題意中的兩個條件句抽成關鍵詞語或公共詞而列成行、列,制成表格,然后將題中的已知量和未知量填入表格中,從中找到他們之間的相等關系而列出方程組.
五、注意利用圖示輔助分析
利用圖示輔助分析就是在為解一些條件比較復雜的應用題尋找相等關系時,把題目中的數量及它們之間的關系,畫成示意圖,然后通過觀察分析圖中的數量,找出各種量之間的內在聯系,從而找出相等關系,借助圖形這些輔助工具,往往使問題更加直觀,容易思考,使問題迎刃而解.
【例5】 有甲、乙、丙三筐蘋果,先從甲筐取出蘋果給乙、丙兩籃,所給的個數等于原來各有的數,然后再由乙給甲、丙兩筐現有個數,最后從丙給甲、乙兩筐現有個數,互給后每個筐里有50個蘋果,求甲、乙、丙三個筐內原有的蘋果數.
分析:設甲筐有蘋果x個,乙筐有蘋果y個,丙筐有蘋果z個,互給后的量變關系用圖示表示如下:
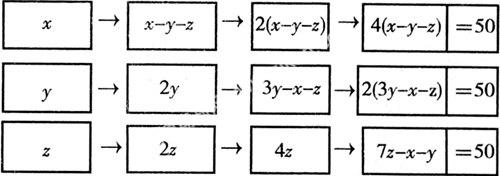
原有蘋果數→從甲取出后→從乙取出后→從丙取出后
這樣按照題設條件的先后順序,步步由圖展示,層次分明,使甲、乙、丙三筐互給后所有蘋果的代數式自然地呈現出來,從而得出方程組.
還有行程問題,工程問題等用直線型示意圖來一分析,比例問題,圓周運動問題等用圓形示意圖來分析.
總之,尋找相等關系的方法要因題而異,但有一點,就是在變化的各未知數中,找不變量,從運動變化的關系中找相等穩定的相等關系,這樣才能使復雜的數學問題簡單化,達到事半功倍的效果.

