《等邊三角形》教學設計與反思

夏寶玉

一、教材分析

《等邊三角形》一課主要是學習等邊三角形的性質定理和判定定理的推理證明和初步應用。本課安排在學生學習軸對稱圖形和等腰三角形有關知識之后，不但可使學生進一步認識特殊的軸對稱圖形—等邊三角形，而且相關定理更是今后證明角相等、線段相等的重要依據。因此，本課內容在教材中處于非常重要的地位，起著承前啟后的作用。

二、教學目標

知識與能力：掌握等邊三角形的定義；理解等邊三角形的性質與判定定理。

過程與方法：在等邊三角形的性質與判定定理的應用過程中培養學生分析問題和解決問題的能力。

情感態度與價值觀：通過對等邊三角形的學習，了解等邊三角形的對稱美，增強學生對生活的熱愛。

三、教學重點

等邊三角形的性質與判定方法。

四、教學難點

等邊三角形的性質與應用。

五、教具：多媒體、用硬紙做的等邊三角形。

六、教法與學法

本課采用探究發現式教學方法，即學生在教師的正確引導下，積極主動參與探索、發現、歸納、類比等一系列數學活動，輕松愉快地獲得知識。

在教學過程中，教師重視學生學法的指導，讓學生在“觀察—發現—論證—歸納”的學習過程中自主參與知識的發生、發展、形成的過程，進而掌握知識的重點難點，培養學生探究問題、交流合作的優良品質。

七、教學過程

（一）導入新課

教師首先利用多媒體展示一組有關等邊三角形的圖片，然后提出問題：房子頂部是什么形狀？這個三角形有何特點？同學們想不想更深入地了解等邊三角形的知識？

（二）自主探究

1．提出問題：（1）根據以往學習圖形的經驗，你認為應從那些方面來研究等邊三角形？（2）試著給出等邊三角形的定義。

2．引導學生展開探究：觀察課前準備的等邊三角形紙片，猜想等邊三角形有哪些性質，并通過測量、折紙、邏輯推理等方式進行驗證；引導學生從角、邊兩方面探究結論。

學生以小組為單位先猜想再交流發表看法，然后教師歸納總結等邊三角形的特點：邊：三邊相等；角：三個角相等，并且都等于60°；性質：等邊三角形三個內角都相等，并且每個角都等于60°。

3．引發學生的進一步思考：（1）在△ABC中，∠A﹦∠B﹦∠C，你能得出AB﹦BC﹦CA嗎？為什么？（2）在△ABC中，AB﹦AC,∠A﹦60°：（a）求證△ABC是等邊三角形；(b)如果把∠A﹦60°，改為∠B﹦60°或∠C﹦60°，結論還成立嗎？（3）你能說出判斷一個三角形是等邊三角形的方法嗎？

4．歸納總結

判定定理：（1）三個角都相等的三角形是等邊三角形； （2）有一個角是60°的等腰三角形是等邊三角形。

（三）實踐應用

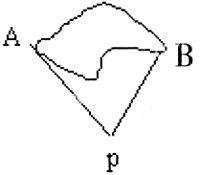
師出示例題：如圖，我校課外興趣小組在一次測量活動中，要測量左圖中池塘最長處的長度，即A、B兩點的距離。測得∠ＡＰＢ＝６０°，ＡＰ＝ＢＰ＝２００m，他們便知道池塘最長處是多少米。猜猜他們測出的長度是多少米，并驗證你的猜想。

學生先獨立猜想池塘最長處為多少米，然后通過小組探究對得出的結論進行驗證。在此基礎上教師進行歸納：在判定三角形是等邊三角形時：若三角形是一般三角形，只要找三個角相等或三條邊相等；若三角形是等腰三角形，一般是找一個角等于６０°

（四）鞏固練習

教材第54頁第1、2題。

（五）歸納小結

通過本節課的學習你有什么收獲？怎樣判定一個三角形是等邊三角形？

（六）作業（略）

（七）教后反思

1．教師講解時按照先剪出等邊三角形，再通過對折的方法讓學生找到邊和角的特點，進而歸納出等邊三角形的特點，使學生較好地掌握這一知識。同時把觀察等邊三角形都是軸對稱圖形，并指出對稱軸的位置這一內容放到課后思考，可使兩種圖形間的異同能夠清晰地顯現出來，更易于學生總結。

2．把學生畫等腰三角形與等邊三角形作為本課的拓展內容。讓學生在完全理解圖形特征的基礎上，進行畫圖操作，有助于提升學生的空間觀念。

3．不足之處是本節課的容量稍大，如果教師在每個教學環節稍作延遲，則可能會影響教學任務的完成。

（責任編輯 李 婧）