二次函數中的數學思想

易小聰

數學思想是數學解題的“靈魂”，總結概括數學思想有利于透徹地理解所學知識，提高獨立分析問題和解決問題的能力。二次函數中隱含著許多重要的數學思想，需要我們去挖掘和運用。歸納起來主要有以下幾種。

一、數形結合思想

數形結合思想就是把數、式與圖形結合起來考慮，用幾何圖形直觀地反映和描述數量關系，用代數方法來分析幾何圖形中蘊含的數量關系，從而使問題巧妙快速解決。解決這類題，首先，要注意學會觀察，提高圖形信息的識別能力，其次，要學會分析和推理，作出正確的判斷。

例1，下圖都是而此函數y=ax2+bx+a2-1 的圖像，若b>0 ，則a 的值等于 （ D ）

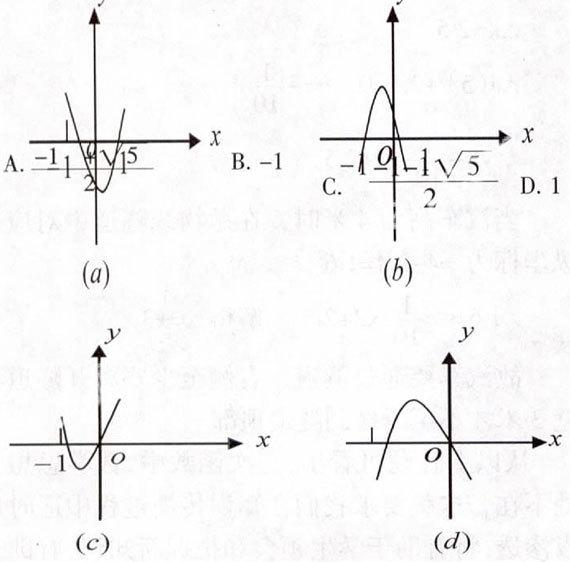
解析：∵b>0，而拋物線（a）（b）中b<0

∴拋物線不可能是（a）（b），

又∵（c）（d）中對稱軸x=-■<0

∴只有（c）f符合

又∵a2-1=0

∴a=1或a=-1（舍去）

∴a的值只能為1，選D

二、函數方程思想

函數方程思想是將數學問題轉化為方程（組），通過解方程（組）或運用方程的性質來分析，轉化問題，使問題得以解決，函數與方程思想是密切相關的。

例2：已知拋物線y=x2 +（2k+1）x-k2+k

（1）求證：此拋物線與X軸有兩個不同的交點。

（2）當k=0 時，求此拋物線與坐標軸的交點坐標。

解析：（1）與X軸有兩個不同的交點，證明方程 ×2+（2k+1）x-k2+k=0有兩個不相等的實數根即可。

（2）通過解方程，求值即可。

解：（1）∵b2-4ac=（2k+1）2-4x（-k2+k）=8k2+1>0

∴方程x2+（2k+1）x-k2+k=0有兩個不相等的實數根。

∴拋物線與 X軸有兩個不同的交點。

（2）當k=0 時，原拋物線為y=x2+x

由x=0 得y=02+0=0

x2+x=0得x1=0，x2=-1

∴此拋物線與 y軸的交點坐標為（0，0），與 X軸的交點坐標為（0，0），（-1，0）。

三、整體思想

整體思想就是根據問題的整體結構特征，把一組數或一個代數式或幾個圖形視為一個整體，去觀察、分析、探究問題的一種方法，從而使問題得以簡捷巧妙的解決。

例3：如圖，矩形ABCD 的長AB=4cm ，寬AD=2cm , op⊥AB是 的中點， ,兩半圓的直徑分別為OA 與OB ，拋物線的頂點是O ，關于OP 對稱且經過 C、D 兩點，求圖中陰影部分面積？

解析：由拋物線頂點是O ，關于 OP對稱且經過 C、 D兩點，根據拋物線、矩形的對稱性可知，S陰=S半圓

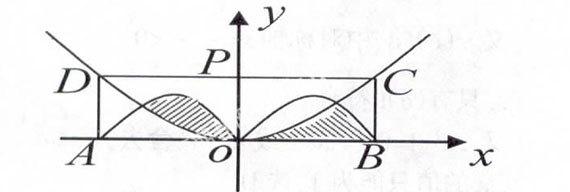
∴s=s=1/2π g=π/2 （cm）

注：解此題的關鍵是運用對稱性，把兩個不規(guī)則的陰影部分視為一個整體。

四、分類討論思想

所謂分類討論思想，就是將要研究的數學對象按照一定的標準劃分為若干類不同的情形，然后再逐步進行研究和求解的一種數學解題思想。對于因存在一些不確定因素，解答無法用統(tǒng)一的方法或者結論不能以統(tǒng)一表述的數學問題，我們往往將問題劃分為若干類來解決。

例4：拋物線 y=x2+2x+k與x軸交點的個數為（）

A.0個

B.1個

C.2個

D.不能確定

解析：求拋物線與 X軸交點的個數由△ 決定 b2-4ac=4-4k， k為未知數，需討論

① k=1時，4-4k=0 ，拋物線與x 軸有一個交點

② k>1時，4-4k>0，拋物線與x 軸有兩個交點

③ k>1時，4-4k<0 ，拋物線與 x軸無交點

∴應選擇D

五、轉化思想

轉化思想是解決數學問題的一種重要思想，在解題過程中，我們往往不是對問題進行正面的直接的攻破，而是把問題進行變形、轉化，把復雜的、生疏的問題轉化為簡潔的、熟悉的，或已經解決了的，或容易解決的問題，從而使問題得到解決，這就是轉化思想。

現實生活中的“拱橋類”問題通常轉化為二次函數來解決。

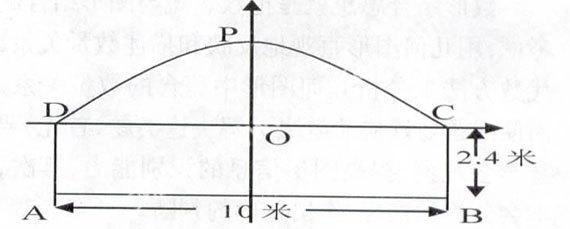
例5：已知一條雙向公路隧道，其橫斷面由拋物線和矩形ABCD的三邊組成，隧道最大高度為4.9米，AB=10米，BC=2.4米，有一輛高為4米，寬為2米，裝有集裝箱的汽車通過隧道，問：如果不考慮其它因素，汽車的右側離開隧道石壁多少米才不至于碰到隧道頂部？

解析：建立恰當的平面直角坐標系可求解。

解：以CD所在直線為 軸，CD中點為原點，建立直角坐標系，則拋物線頂點P在 軸上，所以P（0，2.5），C（5，0），D（-5，0）

設拋物線為y=ax2+k,k即拋物線與y軸交點縱坐標，

∴k=2.5

∴a（5）2+2.5=0

a=-1/10

∴y=-1/10x2+2.5

當汽車高為4米時，在拋物線隧道中對應是縱坐標為 =4-2.4=1.6

∴1．6=- 1/10x2+2.5

解得 x=±3

故汽車要通過隧道，右側至少要離開隧道石壁3米才不至于碰到隧道頂部。

從以上各題可看出，二次函數中，數學思想無處不在，這就要求我們在知識傳播過程中適時加以滲透，將有助于學生領會和把握新知識，有助于提高解題能力，有助于培養(yǎng)和發(fā)展思維能力。