ＳＳＡ到底能不能證明全等

盧文彬

人教版實驗教科書數學八年級上冊第十三章全等三角形13.2三角形全等的條件中,指出已知三角形的兩邊以及一邊的對角對應相等時(SSA)并不能證明兩個三角形全等.但筆者在經過縝密的證明后認為,在比較了兩個三角形的形狀以后,再加上“兩邊以及一邊的對角對應相等”的條件,那就可以馬上判斷出這兩個三角形全等.所以應該在教材中講述如何使用(SSA)證明兩個三角形全等.

人教版實驗教科書八年級數學教材上冊講述的證明三角形全等有很多方法:SSS、SAS、AAS、ASA、HL.大家也知道,SSA,也就是已知三角形的兩邊以及一邊的對角對應相等時并不能證明兩個三角形全等,教材上也給出了相應的反例:

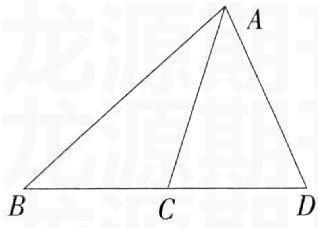
如右圖中的△ABC與△ABD中,AB=AB,AC=AD,∠B=∠B,但是兩個三角形不能重合——不全等.從而給出了結論:已知三角形的兩邊以及一邊的對角對應相等時并不能證明兩個三角形全等.

但是細心的讀者會注意到其實這兩個三角形的形狀不相似(△ABD是銳角三角形,而△ABC是鈍角三角形).如果我們規定了兩個三角形的形狀相似,又已知這兩個三角形的兩邊以及一邊的對角對應相等的情況下,就不能舉出兩個不重合的三角形的例子,從而可以說明這兩個三角形全等.

另外,在實際應用中用公理證明兩個三角形全等之前,自然要判斷這兩個三角形是否可能全等,也就是說要比較這兩個三角形的形狀.顯然,如果在比較了兩個三角形的形狀以后,再加上“兩邊以及一邊的對角對應相等”的條件,那就可以馬上判斷出這兩個三角形全等.

細心的讀者就會發現在證明兩個直角三角形全等的時候還有另外一個特殊的方法:HL,即已知兩個直角三角形的一個直角邊和一個斜邊對應相等的情況下,就可以判斷出這兩個直角三角形全等.從理論上來講,其實HL就是SSA的特例,只不過現在已知的另外一個角是90度而已,用剛才說過的理論即這兩個三角形都是直角三角形,他們的形狀是相同的.

另一方面,我們可以從另一角度證明SSA的正確性.

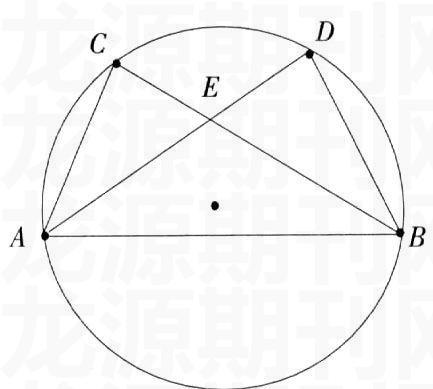
為了研究和△ABC滿足SSA條件的三角形,我們作出它的外接圓(如圖),并以AB為邊,在同側作△ABD,要想使其滿足有一個角相等,只能使點D在圓上,要想有另外一個“非夾邊”對應相等,只能取BD=AC,這樣一來,顯然兩個三角形全等(先證明△ACE與△BDE全等,說明AD=BC,然后用SSS就可以證明這兩個三角形全等了).如果AB恰好是直徑,則可以作出三個滿足SSA的三角形,不過全都與△ABC全等.

綜上所述,筆者認為在八年級階段,既然已經講述了證明兩個三角形全等的方法,那么應該告訴學生這一規律,并且讀者也可以在教輔資料上找到很多用SSA來證明兩個三角形全等的例子(這些題目要用別的方法是很難證明出來的).并且,如果真正把SSA編進教材,在學習證明三角形全等的時候就可以用這樣一句話來總結兩個三角形全等的條件:

已知三個條件,并且至少有一個條件是邊相等的情況下,我們就可以證明這兩個三角形全等.

所以,“SSA”作為全等三角形的判定定理在三角形全等這一章也未嘗不可.

綜上所述,將“SSA”作為全等三角形的判定定理寫入教材,從培養學生探索知識能力出發,這符合新課標上開發學生數學思維,保證學生學習知識的連貫性的要求.當然,如果不至于變動太大,筆者認為至少可以加到閱讀材料上.

責任編輯羅峰