CORDIC算法數字瞬時測頻的FPGA設計與實現
伍小保,王 冰,何 勤
中國電子科技集團公司第三十八研究所,安徽合肥 230088
CORDIC算法數字瞬時測頻的FPGA設計與實現
伍小保,王 冰,何 勤
中國電子科技集團公司第三十八研究所,安徽合肥 230088
數字瞬時測頻(DIFM)技術是現代電子戰中的關鍵技術之一,要求在極短的時間內完成對輸入信號頻率的測量。瞬時測頻的基本思路是將頻率信息轉化為相位信息,再把相位信息轉化為幅度信息,通過對幅度信息量化編碼,從而完成對頻率的測量。本文提出了基于數字下變頻、CORDIC算法相位測量以及相位推算法的數字瞬時測頻方法以及在FPGA中的實現,對單頻信號該方法具有測頻精度高、瞬時性好的優點,特別適合現代電子戰接收機數字瞬時測頻的需求。
數字下變頻;CORDIC算法;數字瞬時測頻;FPGA
0 引言
現代電子戰環境下,雷達、通信信號非常密集,在同一個時間內會有多個信號出現,且頻率覆蓋范圍廣,為實現對這些同時信號的全概率覆蓋,偵察接收機一般采用模擬和數字信道化技術,將一組固定通帶濾波器輸出的數字信號進行快速、寬頻帶、全概率的粗測頻,然后再對各通道中被檢測出的信號進行相對窄帶、高精度的精測頻[1]。信號經過信道化處理后,如果子信道的帶寬取得比較窄,則每個信道輸出一個信號的概率比較大,此時可以采用一些時域測頻算法進行測頻,如相位推算法、瞬時自相關法、曲線擬合法和過零檢測法等方法。其中相位推算法具有運算量小、速度快、精度高、利用很少采樣點就可以實現頻率的估計,特別適合實時處理的場合,因此是DIFM精測頻的比較好的方法。
本文提出了基于數字下變頻的數字正交化、CORDIC算法的相位測量的相位推算法數字瞬時測頻方及其在FPGA中的工程實現,該方法適用于信道化后的單頻信號的高精度、快速頻率測量,在窄脈沖的情況下也可以獲得比較好的測量精度,同時該方法也適用于線性調頻信號的調頻參數測量。
1 CORDIC算法數字瞬時測頻基本原理
CORDIC算法數字瞬時測頻實現的功能框圖如圖1所示,該模塊包括一下幾個主要組成部分:射頻前端、ADC采樣、數字下變頻、CORDIC算法相位測量、相位推算法頻率測量以及脈沖描述字產生等幾個組成部分。
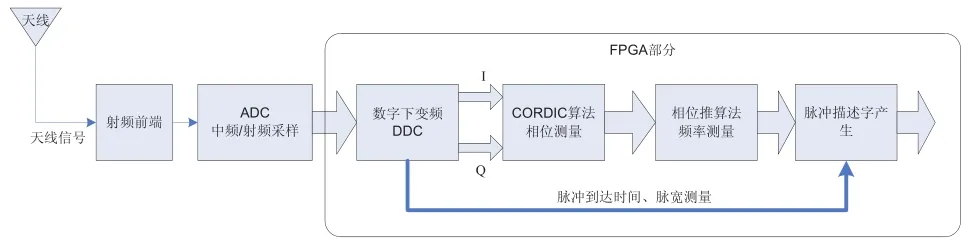
圖1 CORDIC算法數字瞬時測頻系統功能框圖
射頻前端完成天線偵察信號的低噪聲放大、濾波、變頻以及信道化等功能,將信號變換到ADC采樣合適的頻率、帶寬和幅度。數模變換ADC部分完成模擬信號的數字化,考慮到窄脈寬的測量條件以及測頻的瞬時性、精確性,該ADC的采樣率要求比較高,如可以采用TI公司的14位210MHz的ADS5547,對于P波段信號可以進行直接射頻采樣,其它頻段的信號可以通過變頻到一個合適的中頻再進行采樣。
數字瞬時測頻算法等功能都在FPGA中實現,包括數字下變頻采用FPGA實現的優點是其流水線技術可以提高測頻的瞬時性,同時易于高速并行實現以獲得精度更高的脈沖到達時間、脈沖寬度等參數的測量。
1.1 數字下變頻設計
數字下變頻器(DDC)[2]的基本功能是實現信號從數字中頗/射頻搬移到基帶,即從輸入的寬帶高速數據流的數字信號中提取所需的窄帶信號,并濾除帶外噪聲,獲得低速數據流的基帶信號。數字下變頻器使得模擬下變頻存在的混頻器的非線性、本振的頻率穩定度、邊帶和相位噪聲等問題得到解決。DDC的基本結構包括:數控振蕩器NCO、數字混頻器(數字乘法器)、級聯積分梳妝濾波器(CIC)/半帶濾波器(采樣率變換)和低通濾波器,在帶寬相對較寬的情況下沒有CIC濾波器部分,DDC的基本功能原理框圖如圖2所示。
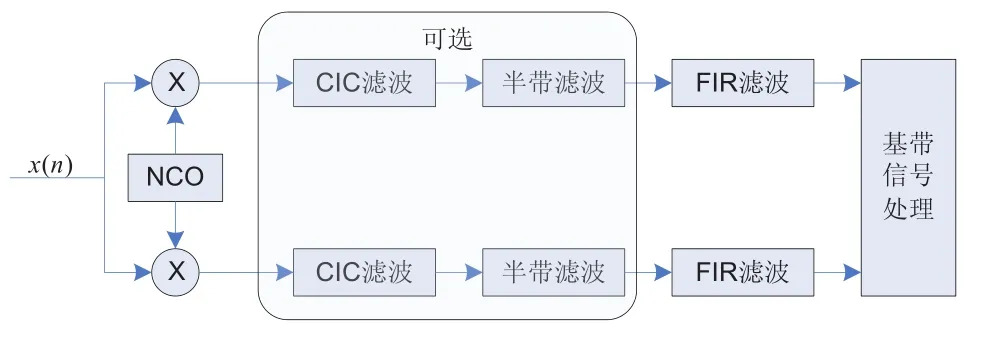
圖2 數字下變頻功能框圖
本設計中DDC采用數字混頻、半帶濾波加FIR濾波實現。數字混頻采用基于CORDIC算法的數字本振NCO設計,該方法特別適合FPGA實現,優點是流水線高速實現,不需要占用FPGA片內ROM,且性能良好。
半帶濾波器適用于抽取率為2n情況,計算效率高,實時性強,HB濾波器的定義為:
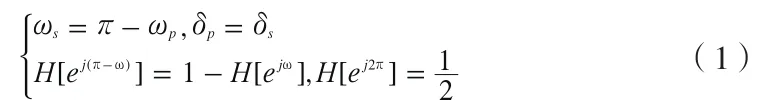
半帶濾波器特性有:1)濾波器偶數序列號(不包括0)沖擊響應為0;2)HB濾波器頻輸出抽取1/2后過渡帶有混疊,通帶無混疊;3)HB濾波器要求通帶和阻帶紋波相等。根據上述特點,以及濾波器系數對稱性,設計的HB濾波器需要的乘法器的數目是普通FIR濾波器的1/4,設計結構采用常用的橫向濾波器結構,適合FPGA中高速實現,一般作為DDC的前級濾波器。本設計中半帶濾波器的輸出采樣率相對比較高,同時輸出為數字檢波信號(去載波信號),因此適合于作為脈沖包絡參數的測量(脈沖到達時間、脈寬等),該測得的參數同時也是數字測頻的同步信號。
DDC中FIR濾波器主要目的是對整個信道進行整形濾波,由于FIR濾波器位于CIC或HB濾波器之后,數據率相對較低,因此階數可以設計的比較高,可以獲得較好的性能(通帶紋波,阻帶衰減以及過渡帶帶寬等)。DDC輸出的高信噪比、高鏡像抑制度I/Q復信號可以作為后續相位測量以及頻率測量的輸入信號。
1.2 CORDIC算法相位測量的設計
相位推算法測頻的基礎是I/Q基帶信號的數字鑒相,傳統數字鑒相的方法是基于ROM查找表法,該方法缺點是當精度要求較高時ROM表非常大,本設計中采用坐標旋轉接收機(CORDIC)算法來實現數字鑒相。
CORDIC算法最早是由J.Voider于1959年提出,包括旋轉和向量兩種模式,可進行向量旋轉、求三角函數、反三角函數和求向量的模等運算,1971年J.Walther提出了統一的改進型CORDIC算法可工作在6種不同的模式,其中CORDIC算法相位測量的基本原理如式2所示:
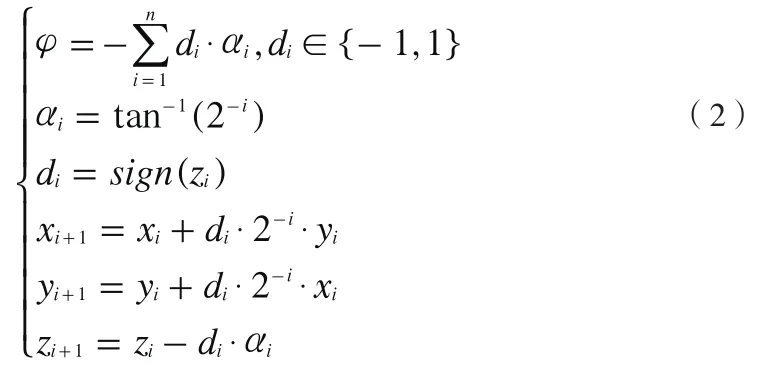
其中(xi,yi)為輸入矢量,(xi+1,yi+1)為輸出矢量di,αi是每次旋轉的角度,di是每次迭代旋轉的方向,旋轉的目標是使z趨近于0。CORDIC算法通過n次微旋轉αi來獲得φ相位值,由zi+1=zi-di·αi,則當n→ ∞,|yn|→ 0,z∞→φ=arctan(y1/x1)從而完成輸入向量(x,y)的相位提取。
由于CORDIC算法可采用流水線型蝶形旋轉結構實現[3],特別適合FPGA技術的實現,同時每級流水線只包括加減法、移位寄存器和tan-1(2-i)系數存儲器,適用FPGA實現時占用的邏輯單元以及存儲器資源比較少,如果輸入的I/Q信號位數足夠高,同時CORDIC算法流水線技術合適,可以獲得高精度的相位輸出。
CORDIC算法獲得的相位值在[-π,π]之間,對于單頻信號隨著樣本點的增加,信號的實際相位會不停跨越周期,因此在頻率計算之前需要對相位進行解模糊,相位解模糊的公式如式(3)所示:
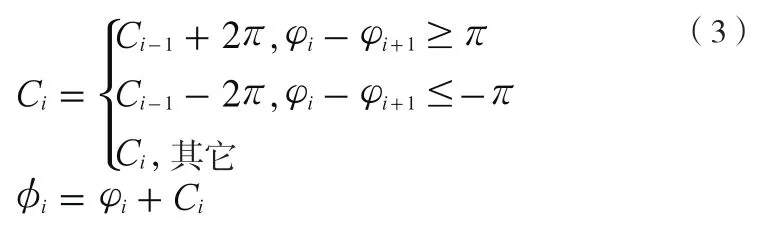
1.3 相位推算法數字瞬時測頻設計
模擬信號的瞬時頻率f(t)與瞬時相位φ(t)的關系為:

則在數字域瞬時頻率和相位的關系為:

其中φi為CORDIC算法計算獲得的第i個樣本點的相位值,Ts為采樣間隔。因此相位推算法頻率測量的基本思路是首先獲得輸入信號的I/Q復信號,通過CORDIC算法獲得瞬時相位值,然后計算相鄰樣本點的相位差,根據相位差以及采樣間隔就可以獲得信號的頻率值。
由于相位推算法測頻對噪聲的影響比較敏感,因此通過多點平均可獲得高精度的頻率。
2 基于FPGA的實現結果
本設計中ADC選擇TI公司的14位ADS5547,采樣率設為200MHz,ADC中頻為425MHz,信號帶寬為48MHz,FPGA選擇ALTEAR公司STRATXI-II系列的EP2SGX60EF1154I4芯片。算法設計中DDC采用一級18階半帶濾波器加一級31階FIR濾波實現,濾波器內部乘法器輸入位寬為18比特,CORDIC算法輸入I/Q信號位寬為18比特,并采用23級流水線實現CORDIC算法相位測量。
測試時輸入頻偏20MHz的單頻脈沖信號,通過FPGA實現以及板級調試,將FPGA的各級輸出結果通過SignaltapII調試工具導入到Matlab中進行分析,結果見圖3和圖4所示。通過實現可見瞬時測頻精度基本在0.1MHz以內,如果通過多點平均,脈沖測頻精度可達100Hz以內(圖4中中間的粗線為誤差均值線)。
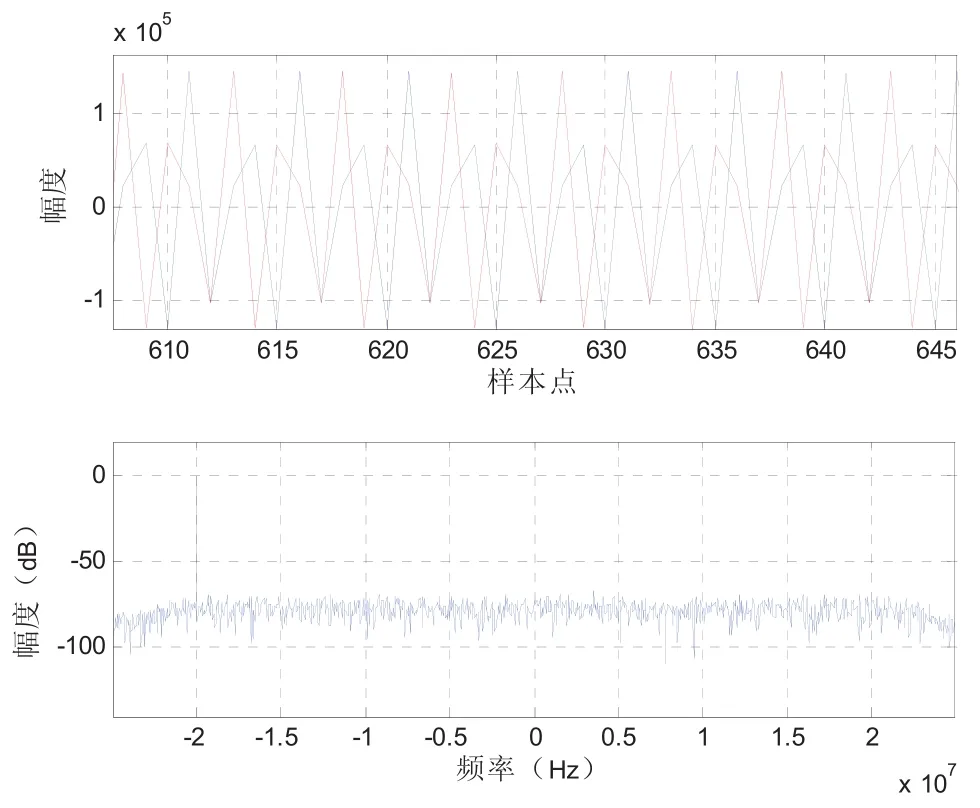
圖3 DDC輸出信號時域和頻譜圖

圖4 CORDIC算法測頻誤差圖
3 結論
本文對對基于CORDIC算法瞬時測頻的FPGA設計與實現進行了詳細的論述,包括各關鍵子模塊設計,并給出了FPGA實現的的結果,從結果看對單頻信號該方法具有測頻精度高、瞬時性好的優點,特別適合現代電子戰接收機數字瞬時測頻的需求。同時該方法已成功應用于某雷達偵察接收機數字瞬時測頻模塊中,獲得了較好的測頻瞬時性和測頻精度。
[1]胡來招著.瞬時測頻[M].國防工業出版社,2002:189.
[2]伍小保,章仁飛,王冰.數字陣列雷達數字下變頻器ASIC 芯片設計[J].雷達科學與技術,2008:496-500.
[3]Andraka Ray. A survey of CORDIC Algorithms for FPGA Based Computers. In Proceedings of the 1998 ACM/ SIGDA Sixth International Symposium on Field Programmable Gate Arrays, 1998:191-200。
TM935
A
1674-6708(2010)22-00199-02
伍小保,工程師,工作單位:中國電子科技集團公司第三十八研究所微波技術部,主要從事雷達接收機及中頻信號處理相關工作 王冰,研究員,工作單位:中國電子科技集團公司第三十八研究所微波技術部,研究方向:雷達、電子戰、通信接收系統,高速數 據采集與信號處理

