計(jì)算機(jī)輔助工程以弧長(zhǎng)為參數(shù)的連續(xù)插值曲線的生成
劉花麗,郝艷莉
(1.鄭州文理專修學(xué)院,鄭州 450001;2.河南職業(yè)技術(shù)學(xué)院,鄭州 450046)
0.引言
1946年 Schoenberg提出樣條函數(shù)的概念,為解決曲線之間的連續(xù)問題提供了可能。參數(shù)樣條曲線曲面即用來描述幾何形狀的樣條方法。1971年法國(guó)雷諾汽車公司的 Bezier提出一種由控制多邊形設(shè)計(jì)曲線的 Bezier參數(shù)曲線方法。1972年,de Boor在總結(jié)前人經(jīng)驗(yàn)的基礎(chǔ)上給出了 B樣條參數(shù)方法,該方法發(fā)展成為應(yīng)用廣泛的B樣條曲線。因此可知參數(shù)的選擇對(duì)曲線的生成是極其重要的。從曲線論出發(fā),曲線的曲率是曲線的內(nèi)在幾何量,曲率的大小代表著曲線的彎曲程度;曲線的弧長(zhǎng)變量是曲線的幾何不變量,它有助于實(shí)現(xiàn)快速、準(zhǔn)確的時(shí)空變換。因此在 GCAD中,諸如機(jī)械加工中刀具的移動(dòng),機(jī)器人沿某一軌道運(yùn)動(dòng)或沿曲線等弧長(zhǎng)分布鉚釘?shù)葘?shí)際工作中都提出了參數(shù)曲線的弧長(zhǎng)參數(shù)化,即以曲線自身不變量的弧長(zhǎng)為參數(shù)建立的方程。在文獻(xiàn)[1]、[2]中,以近似弧長(zhǎng)為參數(shù),這些方法實(shí)際上仍是采用一般參數(shù)作為變量建立方程的,并沒真正的實(shí)現(xiàn)弧長(zhǎng)參數(shù)化。在文獻(xiàn)[3]、[4]、[5]中真正實(shí)現(xiàn)了弧長(zhǎng)參數(shù)化。其中 [3]僅做到了 G1連續(xù)。從其建立曲線方程可以看出他們是一組非線性方程組;對(duì)于求非線性方程組的解來說并不像線性方程組求解那樣有一套成熟的理論來支持它,只能靠數(shù)值方法來解決它,并且針對(duì)個(gè)別問題只能做個(gè)別處理。計(jì)算機(jī)計(jì)算速度的提高為數(shù)值算法提供了有力的保障,為實(shí)現(xiàn)真正的弧長(zhǎng)參數(shù)化提供了求解工具。
數(shù)值方法為計(jì)算方法提供了有力的保證,所以弧長(zhǎng)參數(shù)在曲線插值中的應(yīng)用越來越被看好。本文在文獻(xiàn)[3]的基礎(chǔ)上,將其推廣到 G2連續(xù),并給出了其數(shù)值解的求解方法。
1.平面曲線
將平面曲線看成曲線的撓率為零的空間曲線來進(jìn)行研究,因此討論以平面曲線為主。但是平面曲線有它自身的特殊性。利用平面曲線的特殊性質(zhì),由曲線的相對(duì)曲率和平面曲線的 Frenet公式 (見參考文獻(xiàn)[6]、[7])得到以下定理。
平面曲線基本定理:設(shè)κ(s)為曲線 P(s)的曲率,α(s)為單位切向量,θ(s)為α(s)與 x軸正向夾角,則有:

為了方便其見,將曲線的曲率記為κ,則κγ=±κ,其中“+”表示單位切向量β正好指向曲線彎曲的一側(cè),而“-”表示單位切向量β指向曲線彎曲的一側(cè)。以下討論中曲率的正負(fù)都與此處相同。
對(duì)曲線 P=P(s)在 [a,b]上的插值來說,只需對(duì) [a,b]進(jìn)行劃分:a<s0<s1<…<sn<b。對(duì)?s∈[si,si+1]有:

所以整條插值曲線可以寫成:

下面討論利用 (1)式生成 G2連續(xù)的曲線方程。
2.G2連續(xù)曲線
文獻(xiàn)[3]指出在平面點(diǎn)列間插值,利用已知點(diǎn)的坐標(biāo)和切線角,根據(jù)平面曲線基本定理,反求兩端點(diǎn)處的曲率,在線性曲率條件下生成的曲線只達(dá)到了 G1連續(xù)。下面通過適當(dāng)?shù)募尤胍恍┘僭O(shè)前提條件更進(jìn)一步地利用平面曲線定理,得到的插值曲線達(dá)到 G2連續(xù)。
2.1 分段線性曲率插值曲線
在平面上任給定一組型值點(diǎn){Pi}n0,型值點(diǎn)端點(diǎn)處的曲率為{κi}n0。通過這些型值點(diǎn)建立一條 G2連續(xù)的曲線。根據(jù)幾何樣條曲線的定義,在每?jī)蓚€(gè)型值點(diǎn)之間是一段 cornuqu螺線 (參考文獻(xiàn) [8]),并在整個(gè)樣條上 G2連續(xù)。因此在每?jī)蓚€(gè)型值點(diǎn)之間做曲率關(guān)于弧長(zhǎng)參數(shù)的線性插值。為此首先考慮在兩個(gè)型值點(diǎn)間進(jìn)行曲線插值,為了保持符號(hào)簡(jiǎn)潔,可以再次省略指標(biāo) i;而用 P1、P2代表任意相鄰的兩個(gè)型值點(diǎn)。設(shè)曲線在 P1點(diǎn)的切線角為θ1,曲率為κ1;在 P2點(diǎn)的切線角為θ2,曲率為κ2。為得到一條 G2的曲線,由參考文獻(xiàn)[3]知,直接引用 (1)對(duì)于任意的初始角不一定能得到一條 G2連續(xù)曲線。所以在已知條件下,再引入新的變量,使得對(duì)于給定的θ1、θ2,可以得到一條滿足條件的 G2連續(xù)曲線。假定過此曲線上 P1、P2之間有一自由點(diǎn) Q,且 Q處的曲率為任意可變的,記點(diǎn) Q處的曲率為κ。則把 P1、P2之間分成兩段,對(duì)每一段作線性插值,則在 P1、P2之間分段進(jìn)行曲率線性插值。設(shè) P1Q間的弧長(zhǎng)為 s1,P2Q間的弧長(zhǎng)為 s2且 P1,P2在一條水平線上 (即設(shè) P1,y=p2,y)。

圖 1 插值曲線 (單位化的圖示)
第一段曲線 P1和 Q之間的曲率κ1(s)為線性變化:

則其切線角為:

P1和Q之間的一段 Cornuqu螺線在局部坐標(biāo)系中被表示為關(guān)于弧長(zhǎng) s的參數(shù)方程,當(dāng)積分上限為 s1,就得到 Q出的坐標(biāo)設(shè)為 (x1,y1),則

第二段曲線:與第一段曲線生成相似。
設(shè) Q和 P2之間的曲率κ2(s)為線性變化:

則其切線角為:

P2和Q之間的一段 Cornuqu螺線在局部坐標(biāo)系中被表示為關(guān)于弧長(zhǎng) s的參數(shù)方程,當(dāng)積分上限為 s2,就得到 Q出的坐標(biāo)設(shè)為 (x2,y2),則

2.2 G2連續(xù)的條件
滿足上述條件的解有很多,為了保證插值曲線 G2連續(xù),需要在連接點(diǎn)處加入切線連續(xù)的條件。由弧長(zhǎng)為參數(shù)的曲線切向量為單位切向量知,要討論曲線在一點(diǎn)處的連續(xù)性,只需要討論在此點(diǎn)處的切線方向平行;而切線方向平行有兩種情況:一種是方向相同,一種是方向相反。如果切線方向相反時(shí),構(gòu)成在 Q處左右兩端曲率互為相反數(shù),所以不會(huì)滿足 G2連續(xù)條件。因此只考慮方向相同的情形。切線方向相同即切線角相等,則在 Q處滿足:

又因?yàn)?Q在一個(gè)坐標(biāo)系下的坐標(biāo)是唯一的,則由 (2)和(3)得

(4)、(5)就是曲線 G2連續(xù)的條件。由 (4)和 (5)得在 Q點(diǎn)處 G2連續(xù)滿足以下方程:

將 x1,x2,y1,y2代入上式即得:

得到整條曲線的插值曲線方程:
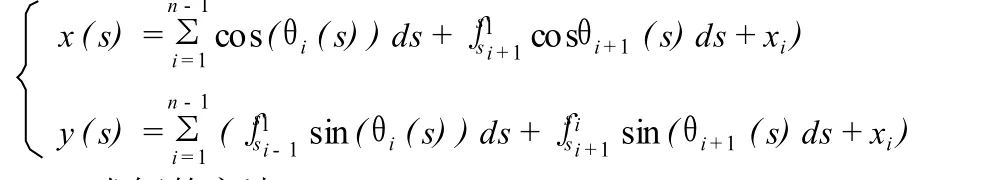
2.3 求解的方法
對(duì)于線性方程組的求解問題已經(jīng)有它的一系列成熟的理論和方法,是非常方便的。但是關(guān)于 s1,s2,κ的方程組為非線性方程組;對(duì)于非線性方程來說沒有成熟的理論來解決,只有借助于數(shù)值的方法來解決。所以解決這種非線性方程組,針對(duì)個(gè)別的問題作個(gè)別處理。對(duì) (7)式要找出一種數(shù)值方法來求其方程組的解。

同理對(duì) x2、y2變形為:

將 (8)和 (9)帶入 (7)即得:

其中:

從 (11)式可以看出 f1,f2,f3,f4是與 s1,s2相關(guān)的,不能用非齊次的線性方程的理論來解決,只能借助于數(shù)值計(jì)算的方法來求解。不妨對(duì) (7)式在給定任意初值的情況下,由計(jì)算機(jī)判斷在迭代過程中 f1f4+f2f3是否為 0,求出方程組的解。
2.4 算法實(shí)現(xiàn)
由 (7)可得:

由 (7)中的第三個(gè)式子可得:

由 (12)和 (13)可以得以下的算法:
第一步:方程組變型為

得出

第二步:先給出 s1,s2的一個(gè)合適的初值;
第四步:把κ得值代入 (14),進(jìn)行進(jìn)行求解。若對(duì)任一個(gè)很小的給定正數(shù)δ,‖a-s1‖≥δ或‖b-s2‖≥δ,則 s1=a,s2=b;循環(huán)從第二步開始執(zhí)行直到‖a-s1‖≥δ或‖as2‖≥δ時(shí)退出循環(huán);若在迭代過程中出現(xiàn)了 f1f4+f2f3=0或 s1,s2互為相反數(shù),說明此初始條件用此方法求解是無解的,退出循環(huán)。
第五步:求得的 a,b即為 s1,s2的值,并由 (8)求出;
第六步:將它們代入原始方程組進(jìn)行畫圖,進(jìn)行整體連接。
3.結(jié)論
本文從微分幾何的觀點(diǎn)入手,實(shí)現(xiàn)了弧長(zhǎng)參數(shù)化,并把插值曲線從 G1連續(xù)推廣到 G2連續(xù);在分段線性曲率條件下得出插值樣條生成過程和實(shí)現(xiàn)方法。在允許存在一定誤差的范圍內(nèi),利用數(shù)值方法求解,在單枝區(qū)間內(nèi)求出的解總是適定的。從以上分析可以看出,在坐標(biāo)系中討論曲線的生成問題,不僅和兩端的曲率有關(guān),也和兩端的切線方向有關(guān)。利用此方法做插值曲線的另一個(gè)好處是可以很方便地得出整條曲線的走勢(shì)和曲線的弧長(zhǎng)長(zhǎng)度,曲線整體和局部的曲率變化;可以很方便的控制曲線的形狀、走向,這是比其他插值方法的優(yōu)越點(diǎn)。在工程上主要用于機(jī)床加工、工程測(cè)量和工程預(yù)算等方面。
[1]李東,李曉明.構(gòu)造曲率法及其在曲線設(shè)計(jì)中的應(yīng)用[J].計(jì)算機(jī)工程與建設(shè),1996,17(1):47-53.
[2]Fang Kui,Cai Fang.C2Continuous Nearly Arc-length Parameterized Curve[J].Numerical mathematics,2003,12(2):143-149.
[3]蔣獻(xiàn)峰,孫毅.平面曲線的曲率表示及其應(yīng)用[J].計(jì)算機(jī)輔助設(shè)計(jì)與圖形學(xué)學(xué)報(bào),1999,11(5):464-466.
[4]吳家驥,楊東英.基于曲率數(shù)據(jù)的曲線擬合方法的研究[J].應(yīng)用科學(xué)學(xué)報(bào),2003,21(3):258-262.
[5]蔣獻(xiàn)峰,孫毅.圓漸開線平面插值樣條及應(yīng)用 [J].計(jì)算機(jī)輔助與圖形學(xué)學(xué)報(bào),2001,12(8):708-711.
[6]陳維桓.微分幾何初步 [M].北京:北京大學(xué)出版社,1990.
[7]梅向明,黃敬之.微分幾何 [M].北京:高等教育出版社,2003.
[8]柳朝陽,周小平.計(jì)算機(jī)圖形學(xué) [M].西安:西安電子工業(yè)出版社,2005.

