考慮負荷周期性和變化率的短期電價預測

劉玉嬌， 蔣傳文

（上海交通大學電子信息與電氣工程學院，上海 200240）

0 引言

近年來電力市場改革的深入突出了電價預測的重要性，很多學者也都研究了很多的方法對中長期或者短期的電價進行預測，取得了顯著成果。目前常見的用于電力預測的方法有時間序列方法［1－2］，神經網絡及其改進算法［3－5］，模糊系統建模方法和其他一些非線性逼近方法等等［6－7］。這些方法都有各自的特點和優勢，也有相應的劣勢，但是從目前應用情況來看，基于神經網絡的算法占據著電價預測研究的主要陣地。

神經網絡是目前采用人工智能方法進行工程計算的中的主要工具之一，其具有適應性強、數學模型簡單等一系列優點，而其主要缺點是收斂比較慢。神經網絡因為有著良好的非線性預測性能，可同時處理多個因子，因此對電價的平均值序列有較好的預測效果。雖然其計算時間稍長，但是由于電價預測基本都是離線進行的，因此，這種計算時間是可以接受的。由此，本文也采用基于神經網絡的電價預測模型，采用美國Pennsylvania-New Jersey-Maryland（PJM）電力市場的數據對市場清算價格（market clearing price，MCP）進行短期預測。

1 網絡基本結構的確立

目前提高神經網絡電價預測結果主要采用改進網絡結構和優化輸入端兩種方法［8－9］，本文采用后一種方法，即通過增加少量的輸入因素和對歷史數據的進一步分析來提高預測結果的精確度。因此，盡管目前有很多優化的神經網絡結構，其提高收斂速度和計算精確度均比傳統神經網絡要好，比如采用模糊學習的神經網絡或結合灰色理論后進行預測［9］，由于本文重點是對網絡的輸入側參數進行改進，為體現一般性，將采用普通的BP神經網絡來進行電價預測。

BP型神經網絡的結構有很多種，3層的BP網絡作為最基本的BP型網絡類別具有較好的多維映射逼近性能，而且3層的網絡結構還有很好的通用性能，因此選擇3層的BP網絡作為網絡的基本結構。網絡的傳遞函數和學習函數也采用比較傳統的函數，網絡的中間層傳遞函數選用S型正切函數，輸出層傳遞函數則采用S型對數函數，學習函數采用低度下降權值/閾值學習函數。

基于以上所述，采用的是一種3層的BP型神經網絡，其結構和數學模型都比較簡單，非常適合工程應用，而且有利于體現所增加的輸入端因子對預測結果影響的一般性。

2 MCP預測模型的建立

2.1 輸入輸出因素的確定

影響電價的因素有很多，比如負荷，天氣，供求關系和其他人為因素等，所有因素中負荷與電價的關系是最密切的，因此采用負荷電價模型來進行電價預測。負荷電價預測模型就是以負荷為神經網絡的輸入，以電價為神經網絡的輸出，一般可選定一個月或更長的時間的歷史數據為樣本來進行預測。

雖然電力系統負荷受多方面影響而具有很大的不確定因素，但是負荷也具有周期性并被直接或間接的使用在電價預測上［5－10］。其最短周期可認為一天，但是從人們正常的生活運作來看，一周為一個基本周期是比較合適的，基本上可以涵蓋除特殊節假日或其他意外情況的所有情況，基于此本文以一周為其基本周期。圖1為美國PJM市場某年2月份每個星期一和星期天的負荷曲線，從圖中可以明顯看到負荷曲線的周期特性。由此可以在網絡的輸入側加入周期性的因素，并采用最簡單的星期值為該周期性元素數值［11］。

圖1 二月份周日和周一負荷曲線Fig．1 Load curve of the Sunday and Monday in February

BP型神經網絡在電價預測方面的一個重大缺點之一就單點的最大偏差太大，甚至達到100%以上，這種情況一般都是發生在電價出現較大波動的時刻。由于預測模型的輸入是基于負荷的，因此采用與負荷相關輸入因素以提高預測精確度是比較合理的選擇［12］。對電價出現較大波動的地方進一步分析，可以發現其一般發生在是電力供求關系變化比較大的時刻。市場環境下的電力供求關系由于有較多的人為因素的存在，其數學模型將非常復雜，因此獲取供求關系變化是比較困難的，因此不宜采用這種因素作為輸入端因子。考慮到供求關系的劇變一般發生在負荷有激增或劇減的時刻，由此直接采用負荷變化率作為輸入以期減少最大時刻誤差。

記 T（d，t）為 d日 t時刻，L（d，t）為 d日 t時刻的負荷，P（d，t）為d日t時刻的MCP，對于某一時刻T（d，t），負荷變化率可以定義為

為了研究負荷變化率和電價變化率的相關性，對二者均做了歸一化處理，并對歸一化處理后的數據進行對比分析，節選二月初數據對比結果如圖2所示。圖2為二月初連續50 h和100 h內，負荷變化率和價格變化率的圖像。由圖中可以看出兩者有著比較好的相關性，因此可用負荷變化率來對單點的預測誤差進行改進。由于電力系統反應較快，因此只有時間間隔比較近的變化率才會起比較大的作用，為此只考慮預測時刻的負荷變化率和前一時刻的負荷變化率。為了同時考慮連續兩個小時內的變化情況，定義某時刻的累加變化率DL1（d，t），計算方法如式（3）所示。由于分別把負荷變化率和累加變化率當作輸入因素輸入神經網絡會使得輸入增加過多，因此定義綜合負荷變化率DLz（d，t）來同時考慮以上兩個方面，其計算方法如式（4）所示。

式（4）中λ1和λ2為權重系數，可以根據預測效果進行調整。

基于以上分析，預測模型的輸入由以下幾部分組成:①預測時刻的負荷、周期性因素、綜合負荷變化率;②前一時刻的負荷、綜合負荷變化率和電價;③前日同時刻的負荷和綜合負荷變化率和電價。

模型輸出為預測時刻的電價。由于需要預測時刻的負荷和變化率作為輸入，因此需要在對負荷進行預測之后才能進行電價預測。采用實際負荷進行預測。

圖2 二月初連續100小時和50小時內的負荷變化率和MCP的變化率曲線圖Fig．2 The curve of change rate of Load and MCP of 100 hours（a）and 50 hours（b）in Early February

2.2 歷史數據的預處理

由于BP型神經網絡計算速度較慢，因此對輸入數據的預處理則顯得尤為重要。對這方面的研究也有很多，如最優訓練樣本選取算法等，本文采用小波分解算法，將歷史數據進行分解成高頻和低頻的不同部分。小波分析是近年來數學方面的重大成果，目前已經廣泛用于數據處理、信號分析、故障診斷和時間序列預測等領域并取得很好的效果，是一種比較成熟的工程數據分析工具。

據前人研究，由于電價和負荷數據的特性，電價預測的歷史數據宜分解為單尺度或二尺度而不宜過高，因此對歷史數據用Daubechies3小波進行單尺度分解。DaubechiesN小波是采用Daubechies方法構造的一系列小波函數，是一種常用的多分辨分析離散小波變換函數，其濾波函數和尺度函數隨N值不同而不同，具有良好的時域和頻域特性。對二月份的負荷和電價分解后的波形比較如圖3和圖4所示，負荷和電價均被分解為概貌波形和細節波形。

圖3 二月份負荷的小波分解波形Fig．3 The result of wavelet analysis for load of February

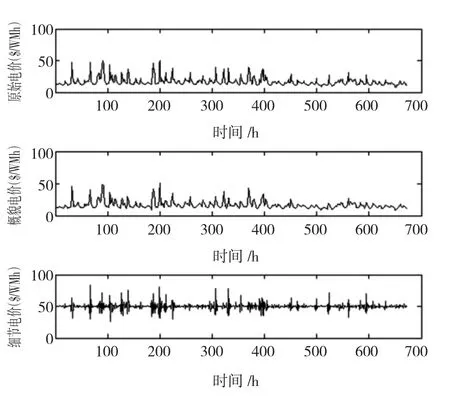
圖4 二月份MCP的小波分解波形Fig．4 The result of wavelet analysis for MCP of February

其中概貌波形（低頻部分）能夠反映負荷和電價的基本特性，從圖中也可以看到其和原始數據的波形比較相像，而細節波形（高頻部分）則更多地反映了數據的局部突變特性。考慮本文已經增加了負荷變化率和周期性因素兩個輸入因子，因此本文采取對高頻和低頻信號分別導入網絡模型進行計算，之后進行疊加，從而獲得最終的預測結果。

3 預測結果分析

為了進行對比，采取普通未采用周期性因素和僅采用周期性因素以及采用了周期性和日綜合負荷變化率的模型進行分析。以二月份電價負荷數據為訓練樣本，預測該月28號各個時段的電價為例，并以平均誤差和最大誤差對幾種方法進行比較。其中各時刻誤差的計算方法采用絕對百分比誤差［6－8］，平均誤差為全天誤差的平均數，記為Eave，單點最大誤差為全天誤差的最大值，記為Emax。

首先采用普通負荷模型進行三次預測，并記該模型為模型1，分別訓練800次，1 000次和3 000次，根據不同學習速率的運算結果比較，選擇學習速率為0.2。其仿真結果如圖5和表1、表2所示。從中可以看到，隨著訓練次數的增加，該方法的預測精確度一直在增加。平均預測誤差分別為10.70%，7.53%和3.62%，而最大誤差則分別為110.24%，43.82%，11.19%。

圖5 模型1的預測結果Fig．5 Forecasting result of Model 1

對同樣的樣本數據采用考慮周期性因素的預測方法進行預測，記為模型2，訓練次數分別為800次，1 000次，3 000次，預測結果如圖6所示。從圖6和表1、表2中可以看到這種模型的收斂速度和預測精確度均比模型1要好。從圖6和表1、表2中也可以看到模型2的平均誤差相比模型1好，但是最大誤差仍然比較大，其三次仿真結果的平均預測誤差分別為7.94%，4.18%和1.16%，最大誤差分別為77.20%、66.28%和9.81%。與模型1相比，其單點最大誤差從11.19%降至9.81%，其平均誤差卻從3.62%降至1.16%，即增加周期性因素后平均預測誤差有了很好的提高。

采用周期因素和負荷變化率因素結合的預測模型進行同樣的預測，記為模型3。此處需要對兩個權值系數進行選取，針對某一日的負荷預測情況可對其進行優化選擇從而得到一個比較理想的輸入參數，簡單處理選擇為0.5。訓練次數仍然采用800次，1 500次和3 000次，其預測結果分別為平均預測誤差分別為7.76%，3.18%和2.34%，而最大誤差則分別為80.57%，35.12%，8.02%。

圖6 模型2的預測結果Fig．6 Forecasting result of Model 2

圖7 模型3的預測結果Fig．7 Forecasting result of Model 3

對比模型2和模型3，可以看到模型3在加入負荷變化率后收斂速度變慢，訓練次數較少時預測結果很不理想。訓練次數為800次時，模型3的平均誤差和模型2基本在同一水平，但是其單點最大誤差并沒有模型2效果好，且加入負荷變化率對單點最大誤差反而有更差的作用，這從另一個角度說明了負荷變化率因素對單點最大誤差是有很強影響的。隨著訓練次數的增加，當達到1500次后，模型3的單點最大誤差明顯好于模型1和模型2，這說明了負荷變化率因素對單點最大誤差的抑制作用。模型3的最終平均預測誤差和單點最大誤差比模型1分別提高了35%和28%，有效的提高了模型的預測精確度。

表1 三種模型預測誤差統計表Table 1 Error Tables of the three models

表2 平均誤差和單點最大誤差統計表Table 2 Tables of Eaveand Emax

4 結語

BP神經網絡在電力系統負荷預測和電價預測中的應用非常廣泛，通過增加負荷的周期性因素和變化率因素對電價預測進行改進。研究結果表明引入負荷周期性因素后可降低模型的平均預測誤差，增加綜合負荷變化率因素則對由電力負荷劇烈變化引起的電價變化有抑制作用，而且負荷的周期性因素還有利于提高模型的收斂速度。針對所采用的預測實例，采用考慮負荷周期性和變化率的預測模型可使平均預測誤差和單點最大預測誤差分別降低35%和28%，這對于提高電價預測的實用價值有很好的作用。預測過程中采用實際負荷作為輸入參數使所得預測精確度較高，當采用負荷預測所得結果作為輸入進行預測時其精確度會有所降低，可采用改進的神經網絡結構來實現的預測精度的進一步提高。

［1］ ANTONIO J Conejo，MIGUEL A Plazas，ROSA Espinola．Day-ahead electricity price forecasting using the wavelet transform and arima models［J］．IEEE Transactions on Power Systems，2005，20（2）:1035－1042．

［2］NEKTARIA V Karakatsani，DEREK W Bunn．Forecasting electricity prices:the impact of fundamentals and time-varying coefficients［J］．International Journal of Forecasting，2008，24:764 －785．

［3］ LI Guang，LIU Chenching．Day-ahead electricity price forecasting in a grid environment［J］．IEEE Transactions on Power Systems，2007，12（1）:266 －274．

［4］ 魏平，李均利，陳剛，等．基于小波分解的改進神經網絡預測方法及應用［J］．電力系統自動化，2004，28（10）:17 －21．

WEI Ping，LI Junli，CHENG Gang，et al．Forecasting MCP using a wavelet-improved neutral network method［J］．Automation of E-lectric Power Systems，2004，28（10）:17 －21．

［5］PARAS Mandal，TOMONOBU Senjyu，NAOMITSU Urasaki．A novel approach to forecast electricity price for pjm using neural network and similar days method［J］．IEEE Transactions on Power Systems，2007，22（4），2058 －2065．

［6］ CHEN Jie，DENG Shijie，HUO Xiaoming．Electricity price curve modeling and forecasting by manifold learning［J］．IEEE Transactions on Power Systems，2009，23（3）:877 －888．

［7］ 張顯，王錫凡，陳芳華，等．分時段的短期電價預測［J］．中國電機工程學報，2005，25（15）:2 －6．

ZHANG Xian，WANG Xifan，CHEN Fanghua，et al．Short-term electricty price forecasting based on period-decoupled price sequence［J］．Proceedings of the CSEE，2005，25（15）:2 －6．

［8］ZHOU Zhi，CHAN Wai Kin Victor．Reducing electricity price forecasting error using seasonality and higher order crossing information［J］．IEEE Transactions on Power Systems，2009，24（3）:1126－1135．

［9］ 朱建良，聞彥，李國輝．基于灰色理論與BP神經網絡的電力系統負荷預報［J］．電機與控制學報，2006，10（4）:440 －442．

ZHU Jianliang，WEN Yan，LI Guohui．The forecasting of the electric power load based on the gray theoryand BP neuron network［J］．Electric Machines and Control，2006，10（4）:440 －442．

［10］ 張顯，王建學，王錫凡，等．考慮多重周期性的短期電價預測［J］．電力系統自動化，2007，31（3）:4 －8．

ZHANG Xian，WANG Jianxue，WANG Xifan，et al．Short-term electricity price forecasting based on price subsequences［J］．Automation of Electric Power Systems，2007，31（3）:4 －8．

［11］ 邵丹，林輝，郝志峰，等．考慮春節影響的中期電量預測［J］．電機與控制學報，2007，11（5）:555 －558．

SHAO Dan，LIN Hui，HAO Zhifeng，et al．Forecasting method of medium-term electricity consumption under the impact from the Spring Festival［J］．Electric Machines and Control，2007，11（5）:555－558．

［12］ BO Rui，LI Fangxing．Probabilistic LMP forecasting considering load uncertainty ［J］．IEEE Transactions on Power Systems，2009，24（3）:1279－1289．

（編輯:劉素菊）