基于小波包的爆炸容器振動分析＊

管永紅，胡八一，黃 超

（中國工程物理研究院流體物理研究所，四川 綿陽621900）

1 引 言

25kg TNT 當量爆炸容器目前是我國最大當量的室內爆炸容器，由于在役運行可能產生較強的地面振動沖擊，因此，對它產生的振動特征的認識十分重要。這種振動信號具有復雜、不規則、突變和衰減快等特點，屬于典型的非平穩隨機信號。對這種信號進行頻譜分析是爆炸研究中的重要研究內容。爆炸振動可以利用多種測試儀器進行實時測量，這些測量結果提供了最原始的振動分布資料。FFT 變換可以對振動分布信號進行頻譜分析，獲得更為直觀的振動信號頻譜分布。然而傳統FFT 分析主要適用于平穩信號的頻譜分析，對于振動信號這類非平穩信號，FFT 分析不是最佳選擇。小波分析是另外1種時頻分析方法，在時域和頻域均具有良好的局部化性質，可以較好地解決時間分辨與頻率分辨之間的矛盾。對于爆炸振動這類非平穩信號，小波分析是1個十分有效的工具。鑒于此，小波變換在爆炸振動信號的分析中得到了廣泛的應用。林大超等［1］利用小波變換的方法對爆炸地震效應振動信號的時變頻譜特征進行了研究，凌同華等［2］將小波變換應用于分析不同頻帶上振動能量分布情況與爆炸發生條件之間的關系，黃文化等［3］將小波變換應用于爆炸振動的安全性分析。本文中，將小波分析應用于25kg TNT 當量爆炸容器的振動信號分析，利用小波包分析方法獲得爆炸容器振動信號在不同位置的時頻特征以及能量分布，為系統的減震設計提供參考依據。

2 小波包分析原理

若ψ（t）∈L2（R），滿足如下允許性條件

則稱ψ（t）為基本小波或母小波，Φ（ω）為ψ（t）的傅立葉變換。由基小波生成的小波函數系可表示為

將信號在這個函數系上進行分解，就得到連續小波變換的定義。

設f（t）∈L2（R），則對它可允許小波函數ψa，b（t）的連續小波變換為

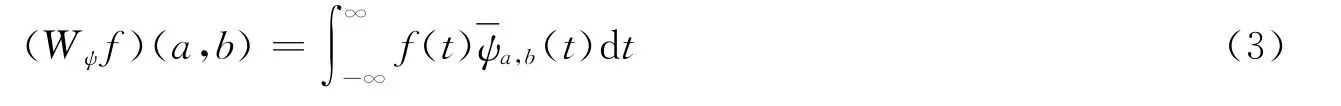
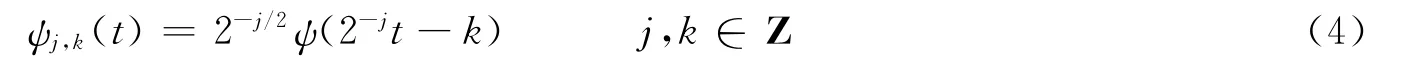
對于給定的函數f（t），離散小波變換系數及其重構公式為

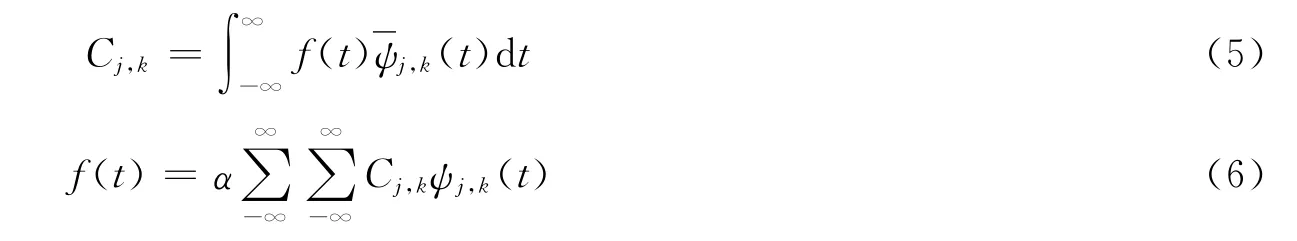
式中：α為與信號無關的常數。

采用2進制小波時，小波分析將信號分解成為低頻與高頻2部分，其中低頻成分又可在下1層分解中分為高頻與低頻成分，如此重復直至滿足要求。函數f（t）與分解的各層成分滿足如下關系

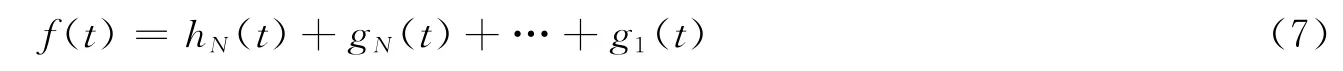
式中：hN（t）為第N 層分解的低頻成分，gi（t）為第i層分解的高頻成分。

小波分析中對各層分解出的高頻成分沒有進一步處理，因此對信號的分析具有局限性。為了克服該局限性，將分解出的高頻成分進行與低頻成分相同的分解處理以得到更精細的分析結果，這種方法稱為小波包分析方法。利用小波包將上1層的信號分解為高頻與低頻2個成分，構成1個二叉子樹。

對于每個能量有限的信號，小波包基可以利用各頻率子帶上的信息提供1種特定的信號編碼和信號重構方法。對給定能量的信號f（t），設頻率分布為0～ωmax，則對它進行i層小波包變換后得到2i個子頻率帶，每個子頻帶的頻率寬度為ω／2i。利用小波包分解系數可以實現對子頻帶范圍信號的重構

總信號可以表示為

式中：fi，j（t）為第i層分解節點（i，j）的重構信號。如果采用2次能量型時頻表示對應每個頻帶上的重構信號，可以定義時頻譜

式中：ωj表示第j 個頻帶的中心頻率，對應的能量

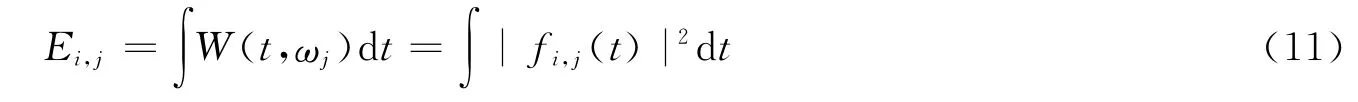
當頻帶劃分足夠細時，頻帶可以被近似認為是連續的頻率分布，式（10）描述了在整個時域和頻域上信號f（t）的連續分布時頻譜，式（11）描述了給定頻率上的能量密度。在原始信號頻率范圍內的集合Ek正好是信號功率譜密度分布規律［4］。

3 爆炸容器產生的地面振動實驗監測結果

爆炸容器及其周邊結構如圖1所示，實驗中炸藥用棉布帶懸于容器中心。根據經驗，在這種情況下水平方向的振動加速幅值很小可以不予考慮，主要考慮垂直方向的振動加速幅值［5］。

實驗中利用加速度計測得的B、C 等2點的波形如圖2所示。信號的采樣周期為10－5s，采樣的點數為51 200點，總的采樣時間為0.512s。根據采樣定理可知，信號的采樣頻率為100kHz，在該采樣率下信號的頻率范圍為0～50kHz。

圖1 爆炸容器及其振動信號測試點布局Fig.1Schematic diagram of an explosion vessel and measured point layout

圖2 不同位置的振動加速波形Fig.2 Vibration acceleration signals measured at different positions

4 振動信號的小波包分析

小波變換中有多種小波基函數可以選擇，同時不同的基函數對分析結果有一定的影響。有很多學者專門就振動問題構造了小波基函數［6］，目前在非平穩振動信號分析中用的較多的是DB8小波基函數，該函數適合于短時非平穩隨機信號的分析，對地震、結構的風載效應、海浪效應等取得了較好的效果［7］。基于此，本文中也選擇該函數作為爆炸容器振動信號分析的小波基函數。原始信號利用DB8小波包經過10級分解后，利用式（6）進行信號重構，圖3為重構信號與實際信號的相對誤差分布。從圖中可以看到重構信號與原始信號高度一致，說明DB8小波非常適合于處理非平穩信號。

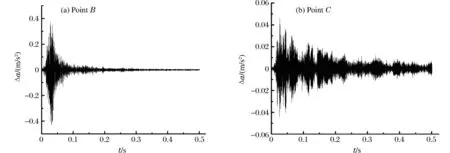
圖3 重構信號誤差分布Fig.3 Vibration acceleration errors of the reconstruction signals at different positions

考慮到原始信號采樣間隔為10－5s以及Nyquest采樣準則，原始信號中最高分析頻率為50kHz。利用DB8小波對原始信號進行10層小波包分解，得到1 024個子頻帶，每個子頻帶對應的頻率間隔為48.8Hz。對每個頻帶利用式（11）計算頻帶能量，得到信號在不同頻帶內的能量分布，見圖4。從圖中可看出，經過爆炸容器隔震措施處理后的振動信號能量主要集中在數個頻帶范圍，在B 點處頻率為約1.5kHz信號的能量分布最大，在C 點則頻率為約2.5kHz信號的能量出現峰值。對圖4所示功率譜進行統計發現，C 點總能量為B 點總能量的2.3%，說明經過隔震溝衰減后，約2.3%的能量被傳遞至隔震溝外。對比不同位置信號的頻譜分布可以看出，隔震溝對振動信號中的低頻成分（2kHz以下）具有很好的衰減效果，而對2kHz以上的信號衰減效果不明顯，這可能與隔震溝的參數（深度、寬度）有關，這一結果與文獻［8］的結果一致，即隔震溝對低頻面波的衰減作用較顯著，對高頻波的衰減作用較弱。

小波分析的最大特點是可以給出信號的不同頻率成分隨時間的變化規律。圖5是利用小波包分析獲得的信號在不同頻帶上的加速度峰值分布，從圖中可以看到不同頻帶的振動峰值。圖6是圖4中對應信號頻率峰值附近頻帶上的重構信號，可以分析不同頻帶信號隨時間的變化規律。利用小波包分析得到的這些信息對爆炸容器的防震設計具有重要的參考價值。

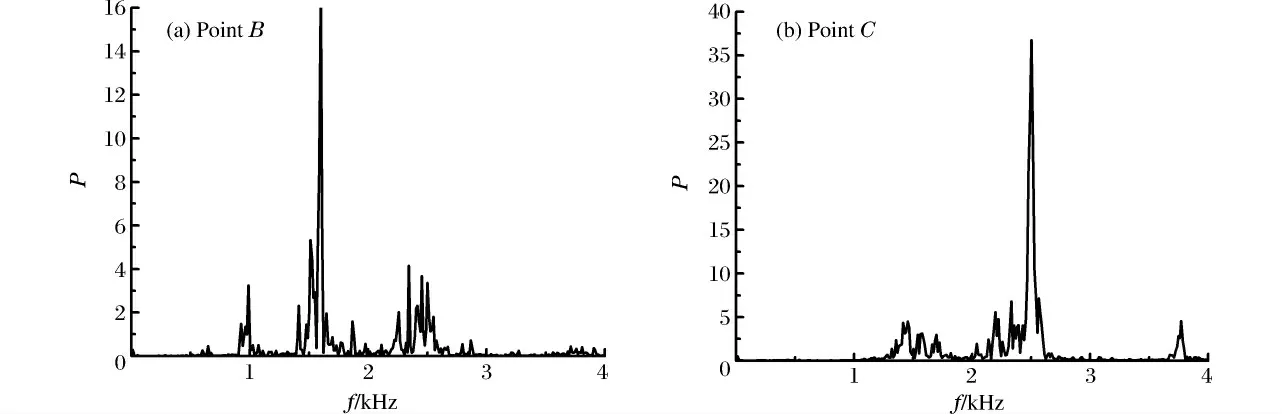
圖4 振動信號的功率譜Fig.4 Power spectra of the vibration signals at different positions

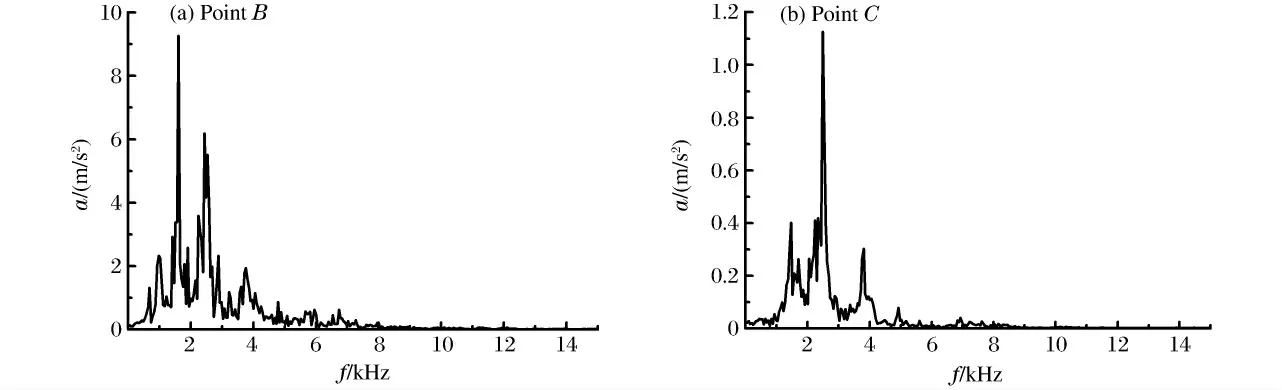
圖5 不同頻帶的峰值加速度分布Fig.5 Maximum acceleration distribution varying with frequency

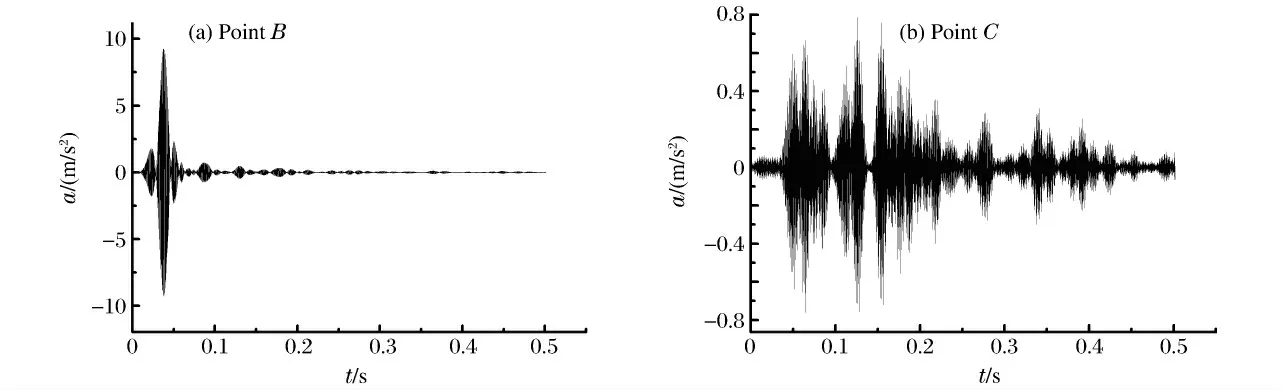
圖6 峰值頻率處的重構信號Fig.6 Vibration acceleration signals reconstructed by the coefficient of maximum power spectral frequency bands

5 結 論

小波包分析可以對已分解的高頻成分作進一步分解，從而提高時間分辨率，具有更好的時頻特性，可以滿足短時非平穩爆炸振動信號時頻分析的需要。

采用DB8小波為基函數的小波包分析方法，分析了25kg TNT 當量爆炸容器振動信號。結果表明，采用的隔震溝使低頻部分信號有大幅度的衰減，傳遞至隔震溝外的信號能量僅占2.3%，同時給出了不同頻帶上的振動峰值以及對應信號頻帶峰值位置上的重構信號，可為系統的防震設計提供參數。

［1］ 林大超，白春華.連續小波變換離散化的爆炸振動特征分析［J］.爆炸與沖擊，2005，25（5）：430－436.LIN Da－chao，BAI Chun－hua.Analysis of blast vibration characteristics by using discretization of continuous wavelet transform［J］.Explosion and Shock Waves，2005，25（5）：430－436.

［2］ 凌同華，李夕兵.地下工程爆破振動信號能量分布特征的小波包分析［J］.爆炸與沖擊，2004，24（1）：63－68.LING Tong－hua，LI Xi－bing.The features of energy distribution for blast vibration signals in underground engineering by wavelet packet analysis［J］.Explosion and Shock Waves，2004，24（1）：63－68.

［3］ 黃文華，徐全軍，沈蔚.小波變換在判斷爆破地震危害中的應用［J］.工程爆破，2001，7（1）：24－27.HUANG Wen－hua，XU Quan－jun，SHEN Wei.Application of wavelet transform in evaluation of blasting vibration damage［J］.Engineering Blasting，2001，7（1），24－27.

［4］ 林大超，施惠基，白春華，等.爆破震動時頻分布的小波包分析［J］.工程爆破，2002，8（2）：1－5.LIN Da－chao，SHI Hui－ji，BAI Chun－hua，et al.On time－frequency distribution of blasting vibration through wavelet packet transform［J］.Engineering Blasting，2002，8（2）：1－5.

［5］ 胡八一，劉倉理，陳石勇，等.25kg TNT 當量爆炸容器的沖擊隔震研究［J］.振動與沖擊，2006，25（6）：43－45.HU Ba－yi，LIU Cang－li，CHEN Shi－yong，et al.Study on isolation of shock induced vibration of a 25kg TNT equivalent explosion vessel［J］.Journal of Vibration and Shock，2006，25（6）：43－45.

［6］ Newland D E.Wavelet analysis of vibration，Part 1—Theory［J］.Journal of Vibration and Acoustic，1994，116（4）：409－416.

［7］ Gurley K，Kareem A.Application of wavelet transforms in earthquake，wind and ocean engineering［J］.Engineering Structures，1999，21（3）：149－167.

［8］ 郭學彬，肖正學，張志呈，等.爆破振動作用的坡面效應［J］.巖石力學與工程學報，2001，20（1）：81－87.GUO Xue－bin，XIAO Zheng－xue，ZHANG Zhi－cheng，et al.Slope effect of blasting vibration［J］.Chinese Journal of Rock Mechanics and Engineering，2001，20（1）：81－87.