鄰近隧道掘進爆破對既有隧道的影響＊

鐘冬望，吳 亮，余 剛

（武漢科技大學冶金工業過程系統科學湖北省重點實驗室，湖北 武漢430081）

1 引 言

隨著國民經濟的發展，對基礎設施建設的需求不斷增加，地下空間的利用得到了空前發展，新建結構物鄰近既有結構物、小凈距平行隧道、上下交叉隧道等形式的近接施工工程大量涌現。由于受到地形地質條件的制約，往往不得不將新建隧道與既有隧道之間的距離設計得很小，因此，在新建隧道施工過程中，既有隧道結構時常遭到破壞，從而危及行車安全。新建隧道施工對既有隧道結構安全的影響主要表現在2個方面，即爆破振動和開挖引起圍巖應力重分布。而對于中硬巖以上圍巖隧道，爆破振動影響較大，如日本的荻津公路隧道、磁浮試驗線上初狩隧道以及意大利的LocooColio公路隧道；而我國的湘黔鐵路增建Ⅱ線坪口隧道、流潭隧道等，也因隧道間距較小，出現過既有隧道襯砌開裂、剝落等危及行車安全等現象［1］，因此對施工技術，特別是爆破開挖施工技術有較高的要求。

目前，對靠近既有建筑物和小凈距隧道等近接工程的爆破振動問題均有研究［2－8］，而對于上下交叉近接隧道的動力影響研究相對較少。本文中，結合在建的貴昆線六盤水至沾益段增建Ⅱ線扒挪塊隧道開挖工程，采用動力有限元，建立3維模型，并參考實際爆破振動速度，對貴昆線獅子口隧道混凝土襯砌的質點振動速度以及應力分布情況進行分析。

2 工程概況

改建鐵路貴昆線六盤水至沾益段增建Ⅱ線工程站前第3標段扒挪塊隧道位于貴州省威寧縣龍場鎮境內，起迄里程DK288＋830～DK292＋258，中心里程DK290＋544，隧道全長3 428m 雙線延米。該段處于陡峭的山體，地表巖溶不發育，僅見溶溝溶縫，隧道處于P1Q＋M 地層，巖性為灰巖夾白云質灰巖，隧道埋深小，未發現地下水露頭，基本無水。

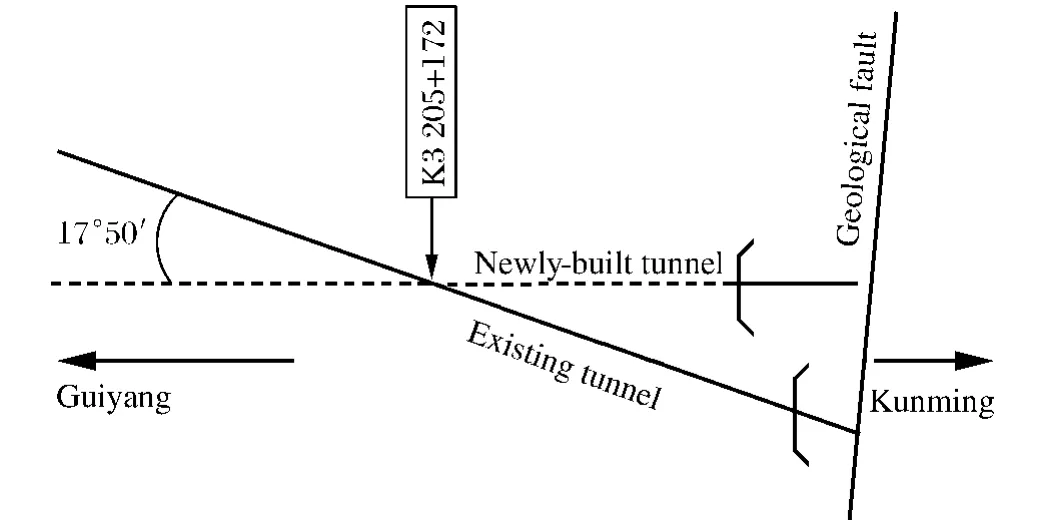
圖1 新建隧道與既有隧道平面相對位置圖Fig.1 Relative position between a newly－built tunnel and an existing adjacent tunnel

既有隧道為電氣化貴昆線獅子口隧道，新建扒挪塊隧道于DK292＋115.3（≈K2 305＋172）處上跨既有線獅子口隧道，夾角17°50′，2 隧軌面高差24.35 m，襯砌外巖層凈距約13.85m，相對位置如圖1所示。

3 計算模型與參數

3.1 計算模型

計算模型采用3維模型。在3維建模時，將開挖隧道縱向作為z 軸，且z 軸經過隧道拱心；y 軸垂直地表。模型各個邊界設置為無反射邊界，隧道已開挖區設為自由邊界，計算模型取為100m×100m×100m，計算模型中隧道中心到各個邊界的距離為50m。開挖隧道下面是既有鐵路隧道，兩者夾角為17°50′，最小距離為13.85 m，交叉處位于模型中部，加載區位于交叉處。計算采用3維實體單元SOLID164，單元總數為65 465，節點數為71 271，模型網格見圖2。

3.2 巖體力學物理指標

計算中圍巖及混凝土的物理力學參數見表1，其中E 為彈性模量，μ 為泊松比，β為內摩擦角，f 為黏聚力，ρ為密度。

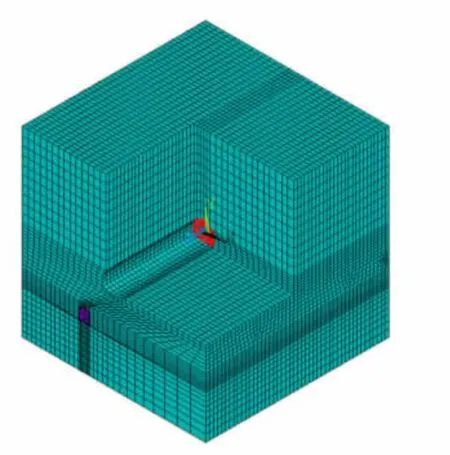
圖2 模型網格Fig.2 Finite element grids of the model

表1 圍巖及混凝土物理力學參數Table 1 Physico－mechanical properties of rock and concrete

3.3 爆破荷載

根據爆破對巖體的破壞和影響的不同，爆破作用范圍可分為近區、中區和遠區。爆破作用近區為巖石粉碎區，爆破作用中區巖體往往產生裂隙破壞，爆破作用遠區巖體只發生彈性振動［9］。對于集中裝藥或單孔柱狀裝藥，采用波動理論，可以近似計算爆破在炮孔壁上的初始峰值應力，進而對爆破振動進行計算。在隧道掘進爆破過程中，一般是分布在一定空間內的多孔裝藥起爆，任意一處由爆破產生的應力是多個應力波疊加的結果，目前還沒有一種理論方法能較準確地計算多孔裝藥起爆在某處產生的應力［7－8］。

根據隧道施工成型的要求，在爆破過程中，應保證隧道圍巖不受破壞，此時圍巖處于彈性振動狀態，因而在建立隧道掘進爆破的振動模型時，可作如下簡化假設［10］：（1）爆破振動荷載以均布壓力荷載形式作用在隧道周壁，作用方向為法線方向；（2）隧道周壁處于爆破作用遠區，隧道周壁的爆破振動荷載不會造成圍巖破壞；（3）爆破振動荷載采用隧道周壁處實測振動波形作為輸入荷載。

爆破安全規程（GB67722－2003）中，爆破振動安全允許標準不僅對振動速度有明確的規定，而且對頻率也有要求。由于三角形脈沖波不能真實反映開挖邊界質點振動的頻率特征，用它作為輸入波進行數值模擬，得到的振動頻率誤差大。為此，借鑒工程抗震研究中地震作用下結構動力響應分析方法，采用隧道周壁處實測振動波形作為輸入荷載。考慮到掏槽爆破產生的振動強度最大，計算時只輸入掏槽爆破的振動波形。掏槽爆破孔深1.4m，單孔藥量為0.55kg，單響藥量為5.5kg，實測波形見圖3。沖擊波的峰值壓力隨距離的衰減關系可近似表現為

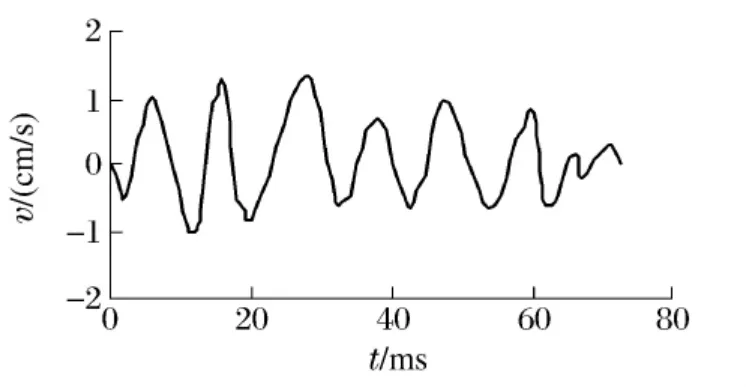
圖3 實測振動速度波形Fig.3 Measured vibration velocity wave form

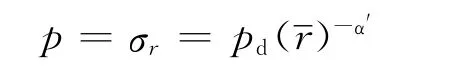
式中：pd為沖擊波作用在巖體上的最大初始沖擊壓力，σr為徑向應力峰值為對炮眼處的對比距離，r為距裝藥中心的距離，rb為炮眼半徑，α′為壓力衰減因數，對于沖擊波區α′≈3或α′＝2＋μ／（1－μ），應力波區α′＝2－μ／（1－μ）。沖擊波的峰值壓力pd計算如下

式中：pd為透射入巖石的沖擊波初始壓力，ρ0、ρm 分別為炸藥的裝藥密度和巖石的密度，cp、D 分別為巖石中的聲速和炸藥的爆速，γ為爆轟產物的膨脹絕熱指數，一般γ＝3。通過試算，確定爆破荷載峰值為20 MPa。

在數值模擬中，采取試算的方法來確定瑞利阻尼參數，具體做法是將試算結果和現場部分實測的有關資料進行比較，然后根據比較結果逐漸調整參數值，最終確定較合適的瑞利阻尼參數。經試算，瑞利常數取α＝0.04，β＝0.003。

4 計算結果及分析

4.1 振動速度分析

由于開挖隧道下面是既有鐵路隧道，兩者夾角為17°50′，最小距離為13.85m，因此，交叉處既有鐵路隧道斷面質點振動情況是考察的重點。在交叉處斷面上選取了4個點，見圖4。A 為拱頂質點，B 為拱與邊墻交點，C 為邊墻中點，D 為底板質點。

通過計算得到各質點振速，見圖5～8。根據爆破應力波的傳播原理，應力波在介質中傳播主要是縱波，在自由面處才形成面波。計算得到隧道拱頂質點垂直振速最大，最大峰值為4.94cm／s，水平向振速很小，vx峰值為0.11cm／s，vz峰值為0.17cm／s。由此可見，到達既有隧道拱頂的應力波主要是縱波，最大振速小于工程要求的5.00cm／s。

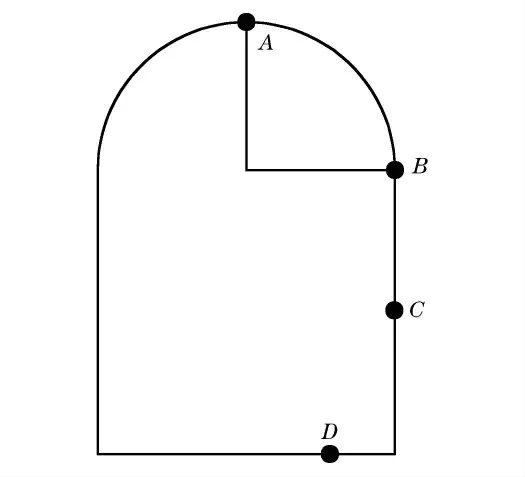
圖4 考察點示意圖Fig.4Sketch map of viewpoints

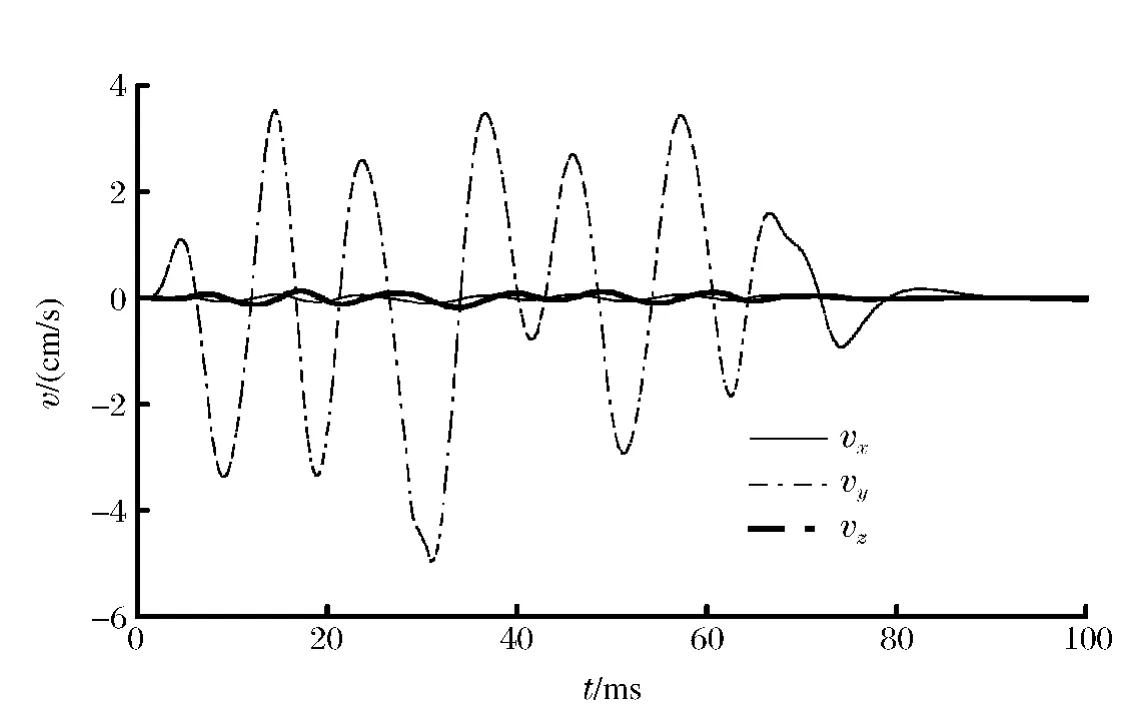
圖5 拱頂質點振速時程曲線Fig.5 Particle velocity curves at the vault crown

隨著應力波向下傳播，受隧道自由面的影響，拱與邊墻交點處質點垂直振速衰減為2.61cm／s，而x方向振速增加較快，其峰值達到1.31cm／s，這主要是瑞利波的作用。在z 方向受軸向圍巖的約束，其峰值為0.22cm／s。在邊墻中點處，應力波進一步衰減，由于面波衰減慢于縱波，此處，x 方向振速為1.06cm／s，而垂直振速已減到1.65cm／s。

底板處，x 方向振速為0.42cm／s，而垂直振速為1.00cm／s。交叉處截面振速峰值分布見圖9。計算表明，垂直振速峰值較大區域主要在拱頂處，并逐漸向下衰減，水平振速峰值向下先增大后減小，垂直振速峰值在截面全域上都大于水平振速峰值。可見，應力波主要以縱波向下傳播，隨著距離的增加逐漸衰減，而在自由面處形成的面波向下傳播先增大，在拱與邊墻交點處達到最大，隨后開始衰減。

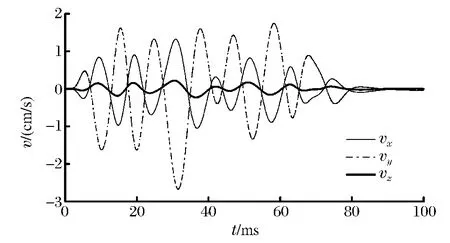
圖6 拱與邊墻交點處質點振速時程曲線Fig.6 Particle velocity curves at the intersection between the arch and the wall

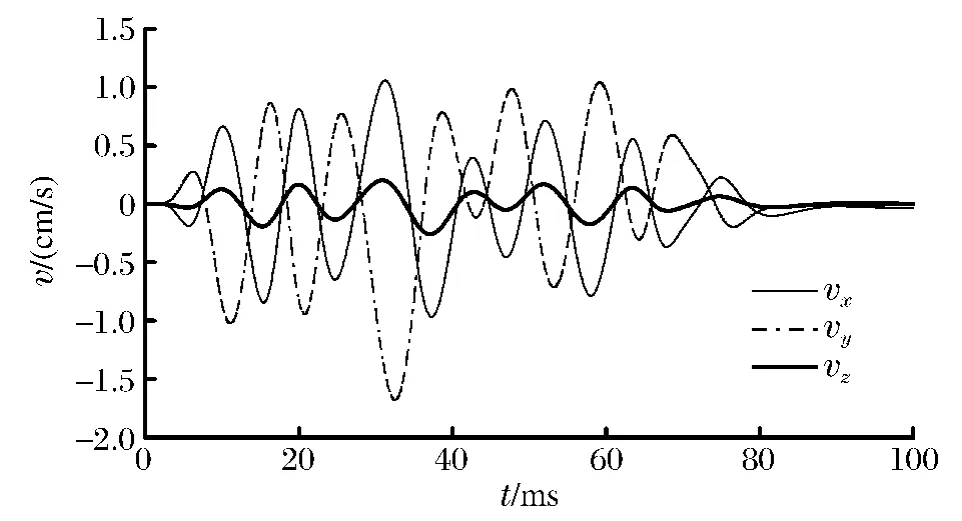
圖7 邊墻中點處質點振速時程曲線Fig.7 Particle velocity curves in the middle of the wall

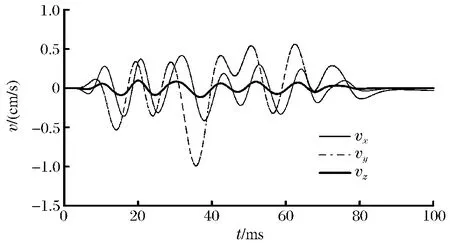
圖8 底板質點振速時程曲線Fig.8 Particle velocity curves at the bottom

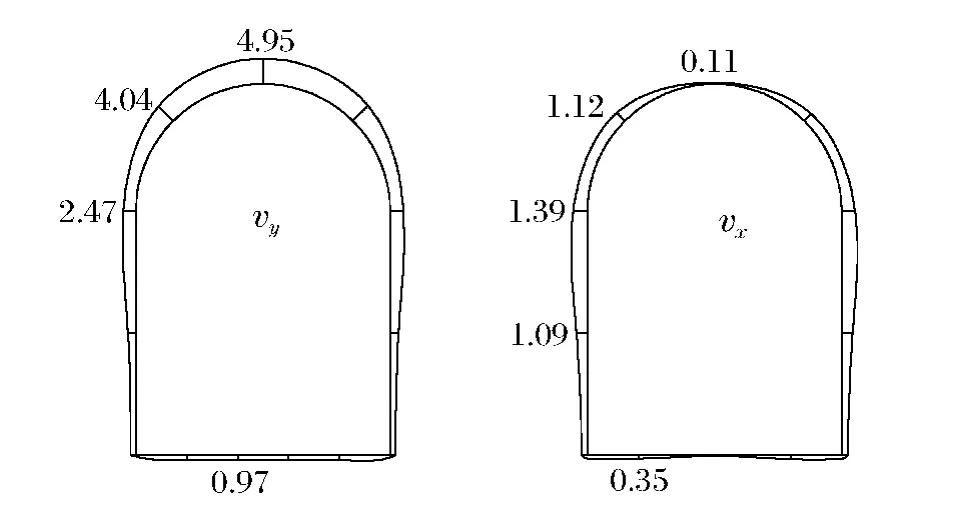
圖9 交叉處截面振速峰值分布示意圖Fig.9Sketch map of particle velocity peak values at the intersection section

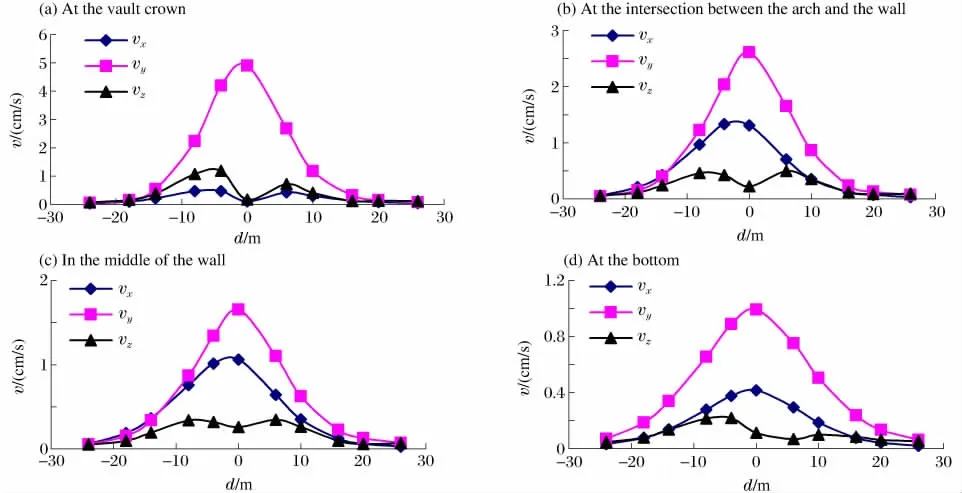
圖10 不同位置處的質點振速峰值隨距離的變化曲線Fig.10 Variation of particle velocity peak values at different positions with distance

為進一步分析爆破對既有隧洞的影響，本文中對既有隧洞軸向分布的各考察點進行了分析。計算結果見圖10。在x 軸向上，正距離為對應已開挖方向，負距離為未開挖方向。垂直振速對應縱波，隨著軸向距離的增加振速不斷衰減，在開挖方向上的衰減指數為0.174 8，見表2。vx與vz振速都是先增加后衰減，可能受到開挖自由面的影響，在未開挖方向的最大峰值大于開挖方向的最大峰值，在開挖方向上的衰減指數分別為0.116 5和0.095 7，兩者衰減指數均小于垂直振速情況。

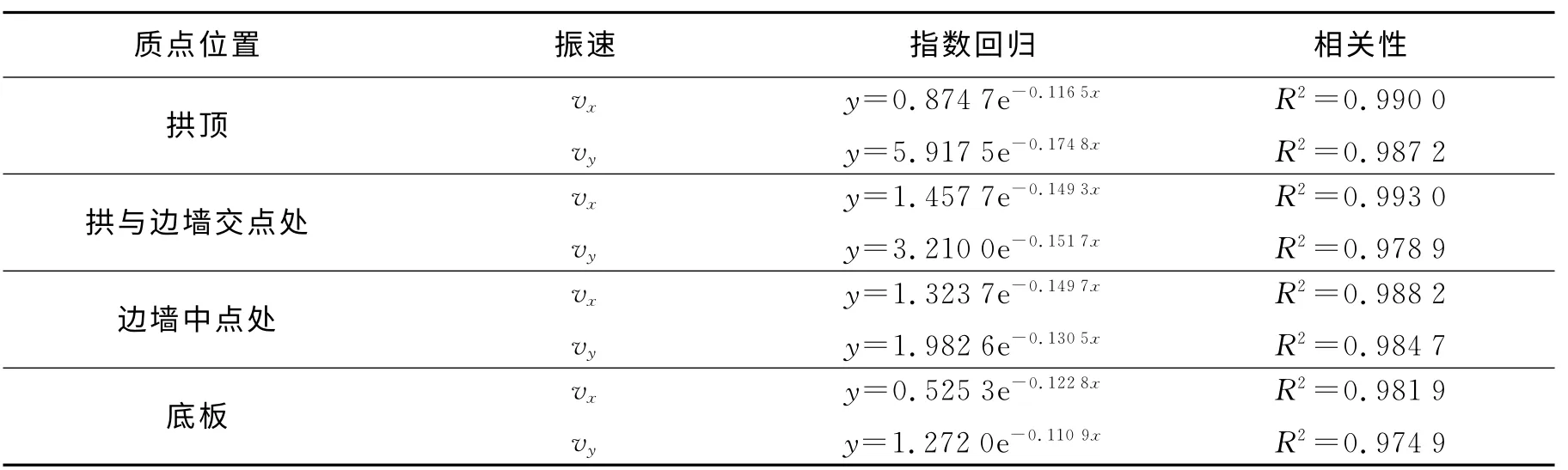
表2 質點振動速度衰減Table 2 Particle vibration velocity attenuation

由圖10可以看出在整個考察范圍內，垂直方向振速峰值比其他2個方向上的振速峰值大，通過回歸分析得出，在拱頂、拱與邊墻交點處，垂直振速沿軸向的衰減指數都大于其他2個方向，在邊墻與底板處，垂直振速沿軸向的衰減指數都小于其他2個方向，衰減公式見表2。x 方向上的振速峰值除了在拱頂處振速先增大后減小，且振速峰值小于z 方向振速峰值外，其他各考察點的質點振速沿軸線不斷衰減，振動峰值也均大于z方向質點振動峰值。z方向振速沿軸線方向均是先增大后減小，主要是表面波引起，其衰減指數均小于其他2個方向的衰減指數。在拱頂與底板處，開挖方向的振速較未開挖方向的振速小，可能與開挖形成的自由面有關。拱頂質點垂直方向振速最大，用薩氏公式回歸得

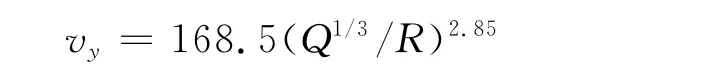
4.2 應力分析

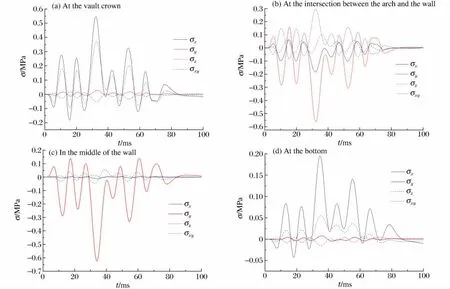
圖11 不同位置單元應力的時程曲線Fig.11Stress－time curves of the elements at different positions

前面主要對爆破荷載作用下既有隧道襯砌質點振速進行了分析，本節將重點分析爆破荷載作用下隧道襯砌的受力情況。LSDYNA 中規定“拉正壓負”。計算結果見圖11。

首先分析交叉處截面拱頂單元應力變化情況，見圖11（a）。計算結果顯示，拱頂單元的x 方向上拉伸應力最大，在32.5ms時達到0.54 MPa，z方向上拉應力峰值次之，為0.36 MPa。可見，在爆炸沖擊荷載作用下拱頂混凝土的破壞主要為x 與z 方向產生的拉伸破壞，因此，當拉伸應力超過混凝土的抗拉強度時，在隧道軸向與橫向會出現拉伸裂紋。

拱與邊墻交點處單元的受力計算結果見圖11（b），可以看出，y 方向的應力最大峰值為0.54 MPa，為壓應力，最大拉伸應力為0.15 MPa，其他方向的拉伸應力均較y 方向的小。在y 方向最大壓應力對應時刻，剪切應力σxy達到最大，為0.28 MPa。若荷載量級上達到破壞混凝土時，在拱與邊墻交點處的隧道襯砌先拉伸后壓剪破壞。

拱頂單元主要受x 和z 方向的拉伸作用，隨著應力波的傳播，在隧道邊墻的破壞主要是y 方向產生的拉伸破壞，見圖11（c）。

計算結果表明，底板處單元主要受x 方向的拉伸作用，其最大峰值為0.20MPa，比拱與邊墻交點處單元以及邊墻中點處單元的拉伸應力峰值都大，見圖11（d）。

對比相對應位置處的質點振速，計算結果表明，雖然整個考察范圍內，垂直方向振速峰值比其他2個方向上的振速峰值大，但在拱頂以及底板的單元主要拉伸應力方向為x 方向，因此，垂直振速不能完全代表圍巖的受力狀況，尤其在交叉處截面拱頂處，x 與z 方向振速基本上為零，而垂直振速很大。

5 結 論

采用動力有限元，建立了3維模型，并參考實際爆破振動速度，反算得到爆破荷載，并計算得到既有隧道圍巖的質點振動速度以及混凝土襯砌的應力分布，分析得到如下結論：

（1）分析了交叉處既有隧道截面質點振動，垂直振速峰值較大區域主要在拱頂處，并逐漸向下衰減，水平振速峰值向下先增大后減小，垂直振速峰值在截面全域上都大于水平振速峰值。此次計算最大振速為4.94cm／s，小于工程要求的5.00cm／s。

（2）對軸向各考察點振速分析得出，在整個考察范圍內，垂直方向振速峰值比其他2個方向上的振速峰值大，通過回歸分析得出，在拱頂、拱與邊墻交點處，垂直振速沿軸向的衰減指數都大于沿其他2個方向的；在邊墻與底板處，垂直振速沿軸向的衰減指數都小于沿其他2個方向的。

（3）在爆炸沖擊荷載作用下，若荷載量級上達到破壞混凝土時，拱頂混凝土的破壞主要為x 與z 方向產生的拉伸破壞，而在拱與邊墻交點處的隧道襯砌先拉伸后壓剪破壞，隨著應力波的傳播，在隧道邊墻的破壞主要受y 方向產生的拉伸應力作用，底板處單元主要受x 方向的拉伸作用而破壞。

（4）對比相對應位置處的質點振速，雖然在整個考察范圍內，垂直方向振速峰值比其他2個方向上的振速峰值大，但在拱頂以及底板的單元的主要拉伸應力方向為x 方向。因此，垂直振速不能完全代表圍巖的受力狀況，尤其在交叉處截面拱頂處，x 與z 方向振速基本上為零，而垂直振速很大。實際工程中，不僅要控制爆破振動速度，而且須進一步分析圍巖的受力狀況，并建立兩者的聯系。

［1］ 王明年，潘曉馬，張成滿，等.鄰近隧道爆破振動響應研究［J］.巖土力學，2004，25（3）：412－414.WANG Ming－nian，PAN Xiao－ma，ZHANG Cheng－man，et al.Study of blasting vibration influence on close－spaced tunnel［J］.Rock and Soil Mechanics，2004，25（3）：412－414.

［2］ 易長平，盧文波.開挖爆破對鄰近隧洞的震動影響研究［J］.工程爆破，2004，10（1）：1－5.YI Chang－ping，LU Wen－bo.A study of the effect of blasting vibration on adjacent tunnel［J］.Engineering Blasting，2004，10（1）：1－5.

［3］ 畢繼紅，鐘建輝.鄰近隧道爆破震動對既有隧道影響的研究［J］.工程爆破，2004，10（4）：69－73.BI Ji－hong，ZHONG Jian－hui.Study on influence of blasting vibration from excavation of a new tunnel on existed tunnel［J］.Engineering Blasting，2004，10（4）：69－73.

［4］ 陽生權.小線間距施工隧道爆破地震影響下既有隧道圍巖線性動力分析［J］.工程爆破，1998，4（1）：1－6.YANG Sheng－quan.Linear dynamic analysis on rock－media of tunnel affected by blasting vibration of new tunnel with small line－clearance［J］.Engineering Blasting，1998，4（1）：1－6.

［5］ 易長平，盧文波，張建華，等.爆破振動對任意形狀地下洞室的影響研究［J］.巖土力學，2007，28（11）：2451－2455.YI Chang－ping，LU Wen－bo，ZHANG Jian－hua，et al.Influence of blasting vibration on arbitrary shape underground chambers［J］.Rock and Soil Mechanics，2007，28（11）：2451－2455.

［6］ 郭建群，張繼春，曹孝君，等.穿越高樓下的淺埋隧道掘進控制爆破技術［J］.爆破，2003，20（1）：28－30.GUO Jian－qun，ZHANG Ji－chun，CAO Xiao－jun，et al.Controlled blasting technique for excavation of the shallow tunnel under high buildings［J］.Blasting，2003，20（1）：28－30.

［7］ 劉慧.近距側爆情況下馬蹄形隧道動態響應特點的研究［J］.爆破與沖擊，2000，20（2）：175－181.LIU Hui.Dynamic responses of hoof－shaped tunnels to adjacent blastings［J］.Explosion and Shock Waves，2000，20（2）：175－181.

［8］ 楊年華，劉慧.近距離爆破引起的隧道周邊震動場［J］.工程爆破，2000，6（2）：6－11.YANG Nian－hua，LIU Hui.Vibration field at tunnel contour induced by a close－in blasting［J］.Engineering Blasting，2000，6（2）：6－11.

［9］ 陶頌林.鑿巖爆破［M］.北京：冶金工業出版社，1986：121－122.

［10］ 曹孝君，張繼春，呂和林，等.淺埋隧道掘進爆破地表震動效應數值模擬［J］.西南交通大學學報，2006，41（6）：680－684.CAO Xiao－jun，ZHANG Ji－chun，LU He－lin，et al.Numerical simulation of ground vibration effects in shallow tunneling blasting［J］.Journal of Southwest Jiaotong University，2006，41（6）：680－684.