裝藥量及水深對水下爆炸氣泡動態特性的影響*

李 健,榮吉利,項大林

(1.北京理工大學宇航學院,北京100081;2.廣西工學院汽車工程系,廣西 柳州545006)

水下爆炸大體可分為3 個階段:裝藥的爆轟、沖擊波的產生和傳播、氣泡的形成和脈動。當爆轟過程結束后,沖擊波以幾倍于水中聲速的速度傳播并首先作用于水中結構,且作用時間短、壓力峰值高,形成對結構的局部破壞,由于氣泡脈動頻率與艦船前幾階固有頻率接近,極易造成船體總體結構的破損或艦載設備的破壞。根據J.R.Blake 等[1]、P.C.Chan 等[2]的研究,多數情況下,在氣泡收縮階段,由于Bjerknes 力作用,氣泡會被水中結構吸引而向結構方向運動,在浮力、慣性力等因素的影響下,沿著氣泡坍塌方向會形成高速射流,且射流會穿透氣泡并沖擊氣泡壁的另一面,最終作用于水中結構并對結構形成再次破壞。隨后氣泡體積收縮至最小并開始第2 次脈動,但能量相對前1 次已經大為降低。因此,水下結構除了受到水中沖擊波的作用外,還會受到氣泡脈動壓力、射流的作用。所以,針對水下爆炸氣泡運動和射流特性的研究對彈藥毀傷威力及目標易損性的評估都具有重要的意義。

J.R.Blake 等[3]、Q.X.Wang 等[4]、Y.L.Zhang 等[5]和C.Wang 等[6]對氣泡的運動特性進行了研究;E.Klaseboer等[7-8]對氣泡與水中結構相互作用進行了實驗研究,并采用邊界元法對氣泡的運動特性進行了研究,驗證了數值計算方法的正確性;A.Pearson 等[9]對單個及2 個氣泡與自由水面相互作用進行了研究,計算結果與實驗結果具有較好的一致性;Z.Zong[10]研究了水中細長梁與短粗梁在氣泡脈動作用下的動力響應;N.Takada 等[11]采用Lattice Boltzmann 方法對剛性壁面附近的氣泡進行了研究,取得了較理想的結果;Y.X.Zong[12]采用邊界積分方法研究了氣泡的運動特性,計算結果與實驗值吻合較好。

邊界元方法只在邊界離散,大大降低了計算成本,但是在氣泡射流產生及與結構相互作用方面有一定的局限性,目前研究成果較少;通常采用與有限元相結合的方法進行氣泡特性的研究。為了對水下爆炸數值模擬研究提供有益的補充,本文中,將以體積加速度模型為基礎,基于MSC.DYTRAN 非線性有限元軟件,應用FORTRAN 語言開發定義流場初始條件和邊界條件的子程序,研究水下爆炸氣泡脈動全過程,并與現有實驗數據進行對比,驗證有限元模型、程序開發和計算的正確性與準確性,并討論裝藥量、水深等因素對氣泡射流速度的影響。

1 理論背景

1.1 氣泡運動初始條件

模擬氣泡的運動,需要先求出氣泡的初始半徑。采用氣泡體積加速度模型來確定氣泡初值,基本思路就是以流場中某一固定點的壓力變化為研究對象,分別研究氣泡體積加速度和炸藥參數與固定點壓力變化之間的關系,聯立求解即可確定氣泡體積加速度與炸藥參數、時間之間的關系。P.A.Frost 等[13]提出了氣泡體積加速度模型

式中:p 為壓力,R 為傳播距離,V 為氣泡體積,ρ為流體密度。式(1)描述了氣泡體積對時間2 次導數與流場壓力的關系,K.S.Hunter[14]為了將體積加速度模型適合于超聲速研究,對式(1)進行適當修正

式中:ac為藥包半徑,A、B 為常數。

由文獻[14-16],流場中壓力、藥包半徑、距離、時間等變量之間的關系為

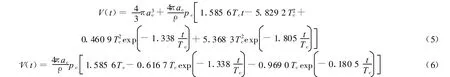
計算結果與文獻[14]中的表達式略有不同。

圖1 為55 g 球形炸藥在3.5 m 水深工況下、t/T c 在0～10 時、氣泡半徑和徑向速度的時程曲線。炸藥起爆后,首先是爆轟過程,壓力瞬間增加,藥包徑向加速度非常大,因此故徑向速度變化率非常明顯,爆轟結束后,膨脹速度逐漸平緩,隨后產物形成的氣泡將以小于聲速向外膨脹。針對這一規律,從圖中觀察,氣泡徑向速度變化率由急速到平緩,因此可以認為當t ＞0.1 ms 時爆轟結束,爆轟產物所形成的氣泡將以小于聲速向外膨脹,可將此刻氣泡半徑值作為氣泡脈動的初值進行計算。

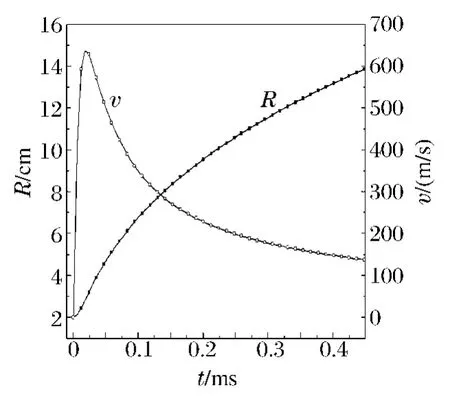
圖1 氣泡半徑及徑向速度時間歷程曲線Fig.1 Time-history curves for radius and velocity of bubble

1.2 狀態方程

忽略氣泡運動對氣體壓力的影響,認為氣泡內的壓力僅和氣泡的初始狀態及其體積有關,即氣泡內的壓力p 與氣泡體積V 的關系為

式中:pc為可冷凝氣體的飽和蒸汽壓,量級與大氣壓相當,一般可忽略;p0和V0分別為氣泡形成時的初始壓力和初始體積;γ為氣體的比熱比,對于TNT 水中爆炸的爆轟產物,γ取1.25。

1.3 經驗公式

氣泡最大半徑的經驗公式為

式中:Rm為氣泡半徑,m;W 為裝藥量,kg;p0為周圍水的靜壓力,Pa;K 為常數。氣泡脈動周期經驗公式為

式中:T 為氣泡的脈動周期,s;W 為氣泡的裝藥量,kg;z0 為氣泡所處位置的流體靜壓的等效水深,m。

根據上述經驗公式,可以計算出氣泡脈動過程中的最大半徑以及脈動周期。

2 數值計算研究

為了驗證數值計算的正確性,首先根據已有實驗數據,對自由水域中氣泡脈動進行數值計算。實驗數據[7]簡單描述如下:實驗在一個直徑約18 m、高7 m 的水池中進行。藥量為55 g 球形炸藥,爆心位置在水池中心水面以下3.5 m 處,并在水池中放入每秒1 000 幀的高速攝影儀拍攝氣泡脈動演變的全物理過程,氣泡演變過程實驗結果如圖2 所示。

圖2 55 g 炸藥水下3.5 m 處爆炸氣泡實驗結果Fig.2 Bubble shape evolution under the 55 g charge mass at the depth of 3.5 m f rom experiment

2.1 有限元模型

對于水下爆炸來說,沖擊波是以指數形式衰減的,48%的能量在25 個藥包半徑的體積內散逸掉[17]。對于上述實驗,由于爆心到自由界面、爆炸池底部及爆炸池壁面的距離均遠大于25 倍藥包半徑,因此,計算將不考慮沖擊波反射效應。計算模型是一個邊長為1.5 m 的正方體。流場采用歐拉單元描述,炸藥位于模型正中部。網格采用中間密、四周疏的分布方式,即爆心處網格最密。爆心處單元對角線長度為55 g 藥包半徑的約0.3 倍,10 g 藥包半徑的約0.53 倍,最大單元對角線長度為藥包半徑的約1.5 倍。

2.2 初始條件及邊界條件定義

數值計算不但要確定氣泡初值,還要確定流場的初始條件和邊界條件。MSC.DYTRAN 并不能通過直接定義重力加速度實現流場靜水壓力的定義,而條件透射邊界(即當邊界兩側出現壓力差時,流體會從高壓區通過邊界流向低壓區)不能直接在單元表面進行定義。因此,將根據初值及邊界條件特點,采用FORTRAN 語言,根據軟件提供的定義初值和邊條的子程序接口EXINIT 及EXFLOW2 定義流場的初值和邊界條件。通過EXINIT 子程序求出每個流場單元所處水深的靜水壓力值,結合相應的變換將數值賦予每個流場單元。同理可以通過EXFLOW2 將流場對應的壓力值賦到流場邊界上。

2.3 與實驗結果對比

圖3 55 g 炸藥水下3.5 m 處爆炸氣泡計算結果Fig.3 Bubble shape evolution under the 55 g charge mass at the depth of 3.5 m f rom calculation

為了更好地對比數值計算與實驗實測的氣泡形狀,盡可能與實驗同步比較,計算結果如圖3 所示。從圖可以看到氣泡在第1 次脈動周期內的全過程,且當氣泡收縮到體積最小時,由于此刻浮力作用,氣泡坍塌從底部開始,隨即產生指向自由界面的射流。對比圖2～3 可以看到,在t=96 ms 前,有限元計算結果與實驗結果具有高度的一致性。觀察實驗結果,對于氣泡后續的運動,由于周圍的引線裝置,對氣泡的運動產生了一定的影響,且圖像相對較模糊,因此與數值計算結果產生了一定的偏差。縱觀氣泡演變的全過程,計算結果與實驗結果吻合相當好。

E.Klaseboer 等[7]不但分別對10、35 和55 g 球形裝藥在水下3.5 m 處進了實驗研究,而且還采了邊界積分方法對氣泡運動進行了數值模擬。本文中采用了有限元方法對以上各工況進行數值模擬,并將計算結果與邊界元、實驗結果進行對比,如圖4 所示。從圖中可以看出,本文的計算結果比文獻[7]中所采用的邊界積分法的計算結果更接近于實驗值。特別隨著裝藥量的增加,計算值與實驗結果具有高度的一致性,隨著藥量的減小,誤差也相應有所增加,此現象與有限元網格密度有關。

表1 為3 種裝藥量下,分別采用實驗測試、有限元和邊界元3 種方法對氣泡第1 次脈動周期內最大體積和誤差。從表中可以看到,有限元計算結果在各種工況下較邊界元計算結果要更接近于實驗結果,且誤差均能保持在10%以內。二者與實驗結果的誤差趨勢基本一致,即隨著裝藥量的減小,數值計算精度會有所降低。以上3 種工況采用了完全相同的有限元模型,因此,隨著裝藥量的減小,有限元模型的網格密度相對降低了,從而數值計算結果的精度也有所降低。因此,若要提高數值計算精度,應當適當提高有限元網格密度。

表1 實驗測量、有限元及邊界元計算結果的比較Table 1 Comparison of bubble volume among the FEA,BEM and experiment

圖4 計算結果與實驗結果的對比Fig.4 Comparison of bubble volume between experiment and calculation

3 特征參數對氣泡動態特性的影響

3.1 裝藥量對氣泡動態特性的影響

為了研究裝藥量變化對氣泡動態特性的影響,以爆心位于水下100 m 處、球形藥包質量在50 ～500 kg 變化系列工況為研究對象,計算氣泡的體積、脈動周期、最大半徑以及射流速度。圖5 為500 kg 炸藥在水下100 m 處氣泡脈動與射流形成過程。從圖中可以看到,氣泡在脈動過程中會逐漸向自由面移動,當氣泡在第1 次收縮到體積最小時,坍塌從氣泡底端開始,產生指向自由面的射流,射流速度增加較快,并在336 ms 時擊穿氣泡,此后,氣泡將以環狀形式膨脹。

圖5 500 kg 炸藥水下100 m 爆炸氣泡脈動過程Fig.5 Evolutions of bubble for 500 kg detonation at the depth of 100 m from calculation

圖6 為相同水深不同裝藥量情況下氣泡體積的時間歷程曲線。對比各工況下相應時刻的氣泡體積可以看到,在爆心位置相同的情況下,氣泡最大體積隨著裝藥量的增加而增加;對于相同裝藥量,在對應的脈動周期內,氣泡的體積會隨著脈動的進行而減小。根據氣泡體積變化曲線還可以提取氣泡脈動的周期,并將數值計算結果與經驗公式進行對比,結果如圖7 所示。從圖中可知,在爆心位置相同的情況下,氣泡脈動周期會隨著裝藥量的增加而增加。數值計算結果與經驗公式的誤差保持在6.9%～10.8%之間。

圖8 為不同藥量所對應的氣泡最大半徑。從圖中可以看到,氣泡最大半徑隨著裝藥量的增加而增加,與經驗公式(9)對比后發現,數值計算結果與經驗公式的誤差較小。從氣泡脈動周期以及最大半徑與經驗公式的對比中可以發現,數值計算結果與經驗公式趨勢一致,誤差較小,證明了數值計算結果的正確性。

圖9 為氣泡形成直至被射流擊穿變成環狀氣泡過程中,正下方壁面運動速度的時間歷程曲線,以垂直向上為正。從圖中可以看到,氣泡具有負向初速度,但速度大小會隨著時間的推移而逐漸減小,在經過一段較平緩的變化后,氣泡壁的速度會迅速增加。氣泡的運動周期增大,氣泡的射流速度降低;藥量減小,射流速度增大。也就是說,小藥量的藥包爆炸產生的射流可能對結構造成嚴重的局部毀傷,射流速度可達數百米每秒,而大裝藥量藥包爆炸形成的射流速度低,但射流影響區域很寬,對艦船結構造成總體破壞。

圖6 氣泡體積時間歷程曲線Fig.6 Volume-time curves of bubbles under different charges

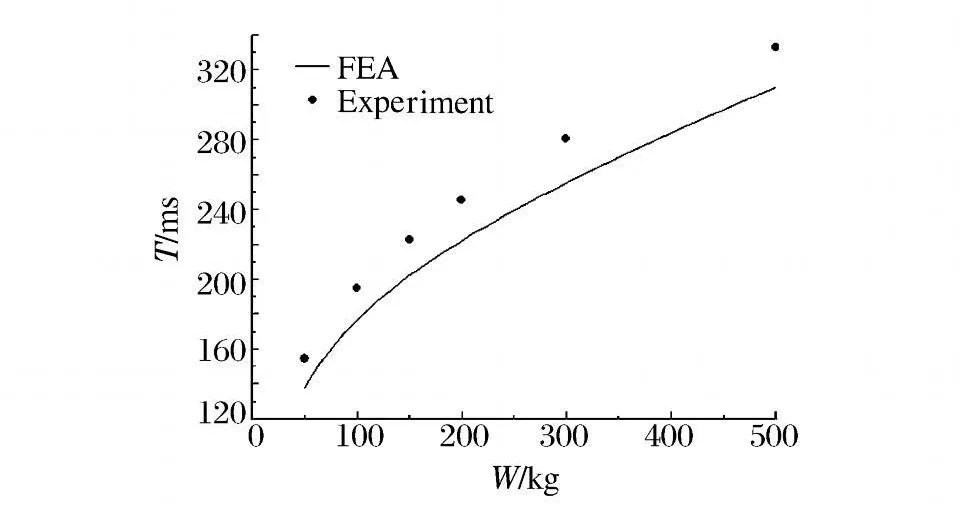
圖7 不同裝藥量時氣泡周期Fig.7 Period of bubbles under different charges

圖8 不同裝藥量時氣泡最大半徑Fig.8 Maximal radius of bubbles under different charges

圖9 氣泡射流速度時間歷程曲線Fig.9 Velocity-time curves of jets under different charges

3.2 水深對氣泡動態特性的影響

為了考察水深的變化對氣泡動態行為的影響,假定系列工況藥量均為100 kg,爆炸水深從25 m 變化到125 m,計算不同水深情況下氣泡體積、脈動周期、最大半徑以及射流速度。各工況下氣泡脈動以及射流形成過程與圖5 類似。計算結果如圖10 ～13 所示。

從圖10 中可以看出,隨著水深的增加,氣泡各脈動周期內所對應時刻處的體積會不斷減小。根據圖10 中氣泡體積變化,提取出氣泡脈動周期,并將計算結果與經驗公式進行對比,對比結果如圖11 所示。從圖中可以看到,氣泡脈動周期隨著爆心初始水深的增加而減小,計算結果與經驗公式的誤差較小。根據圖10 中第1 次脈動周期內氣泡最大體積計算出氣泡等效半徑,如圖12 所示。從圖中可以看出,隨著水深的增加,氣泡的最大半徑同樣會有所減小,對比計算結果與經驗公式,二者具有較好的一致性,平均誤差在4%左右。

圖10 氣泡體積時間歷程曲線Fig.10 Volume-time curves of bubbles at different depths

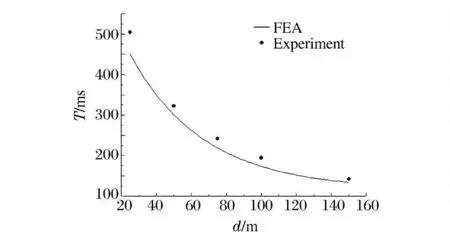
圖11 不同水深時氣泡周期Fig.11 Periods of bubbles at different depths

圖13 為藥量相同、爆心初始位置不同情況下,氣泡正下方壁面運動速度的時間歷程曲線。從圖中可以看到,射流速度隨著水深的增加而增加。也就是說,水越深,氣泡射流載荷的局部效應越明顯;相反,近水面爆炸所產生的氣泡射流載荷速度降低,但射流影響區域變寬,因而總體破壞效應變明顯。所以深水爆炸和淺水爆炸時氣泡載荷對結構的破壞機理不同。深水爆炸氣泡坍塌所產生的射流載荷能引起水中結構的局部破壞,而淺水爆炸泡射流載荷由于影響區域很寬,可引起結構的總體破壞。

圖12 不同水深時氣泡最大半徑Fig.12 Maximal radii of bubbles at different depths

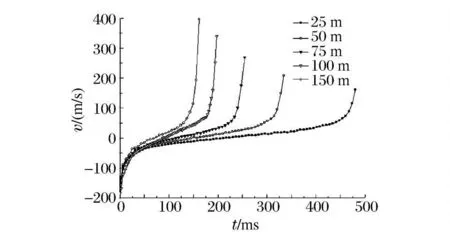
圖13 氣泡射流速度時間歷程曲線Fig.13 Velocity-time curves of jets at different depths

4 結 論

基于氣泡體積加速度模型,采用FORT RAN 語言開發了定義流場初始條件和邊界條件的子程序,并結合MSC.DYTRAN 非線性有限元軟件對水下爆炸氣泡在自由水域中的運動特性進行數值模擬,計算結果與實驗結果具有較好的一致性。分析總結不同水深及不同裝藥量等多種工況下水爆炸氣泡動態特性,得到了以下主要建議及結論。

(1)水下爆炸包括裝藥的爆轟、沖擊波的產生與傳播、氣泡的形成及脈動,三者雖然時間尺度上具有較大差異,但三者在時間上具有連續性,基于流場壓力分布提出的氣泡體積加速度適合于計算水下爆炸氣泡初始條件的確定。

(2)基于MSC.DYTRAN 非線性有限元軟件下開發的定義流場初始條件和邊界條件的子程序EXINIT 和EXFLOW2,可以準確的計算出水下爆炸氣泡脈動的全物理過程,且滿足計算精度要求。

(3)氣泡的運動體積、最大半徑及周期隨著裝藥量的增加而增加,變化范圍較大;但隨著裝藥量的增大,氣泡射流速度減小,持續時間長。即小藥量藥包的氣泡坍塌所產生的射流可能對結構造成局部毀傷,而大藥量藥包氣泡坍塌所形成的射流速度相對較低,但射流影響區域很寬,對艦船結構造成總體破壞。

(4)氣泡體積、最大半徑以及脈動周期隨著水深的增加而減小,且變化較大。隨著水深的增大,氣泡坍塌所產生的射流速度增大,持續時間短,即水越深,氣泡射流載荷的局部效應越明顯,能夠造成水中結構的局部毀傷;水越淺,氣泡的射流載荷速度相對較低,射流影響區域變寬,持續時間長,對水中結構的總體破壞效應越明顯。

[1] Blake J R, Taib B B,Doherty G.Transient cavities near boundaries.Part I:Rigid boundary[J].Journal of Fluid Mechanics,1986,170:479-497.

[2] Chan P C, Kan K K,Stuhmiller J M A.Computational study of bubble-structure interaction[J].Journal of Fluids Engineering,2000,122:783-790.

[3] Blake J R, Gibson D C.Cavitation bubbles near boundaries[J].Fluid Mechanics, 1987,19(1):99-123.

[4] Wang Q X,Yeo K S, Khoo B C, et al.Nonlinear interaction between gas bubble and free surface[J].Computers and Fluids, 1996,25(7):607-628.

[5] Zhang Y L, Yeo K S, Khoo B C, et al.Three-dimensional computation of bubbles near a free surface[J].Journal of Com putational Physics, 1998,146(1):105-123.

[6] Wang C, Khoo B C.An indirect boundary element method for three-dimensional explosion bubbles[J].Journal of Computational Physics,2004,194(2):451-480.

[7] Klaseboer E, Hung K C,Wang C,et al.Experimental and numerical investigation of the dynamics of an underwater explosion bubble near a resilient/rigid structure[J].Journal of Fluid Mechanics,2005,537:387-413.

[8] Klaseboer E, Khoo B C,H ung K C.Dynamics of an oscillating bubble near a floating structure[J].Journal of Fluids and Structures, 2005,21:395-412.

[9] Pearson A,Cox E,Blake J R,et al.Bubble interactions near a f ree surface[J].Engineering Analysis with Boundary Elements, 2004,28:295-313.

[10] Zong Z.A hydroplastic analysis of a free-free beam floating on w ater subjected to an underw ater bubble[J].Journal of Fluids and St ructures, 2005,20:359-372.

[11] Takada N,Misawa M, Tomiyama A,et al.Numerical simulation of two-and three-dimensional tw o-phase fluid motion by lattice Boltzmann method[J].Computer Physics Communications,2000,129:233-246.

[12] Zong Y X, Reginald B H.An improved model for bubble formation using the boundary-integral method[J].Chemical Engineering Science,2005,60(1):179-186.

[13] Frost P A, H arper E Y.Acoustic radiation from surfaces oscillating at large amplitude and small mach number[J].The Journal of the Acoustical Society of America,1975,58(2):318-325.

[14] Hunter K S.Global-shape-function models of an underw ater explosion bubble[D].Boulder:University of Colorado,2001.

[15] Geers T L, Hunter K S.Pressure and velocity fields produced by an underw ater explosion[J].The Journal of the Acoustical Society of America, 2004,115(4):1483-1496.

[16] Hunter K S,Geers T L.An integrated wave-effects model for an underw ater explosion bubble[J].The Journal of the Acoustical Society of America,2002,111(4):1584-1601.

[17] Cole R H.Underw ater explosions[M].US:Princeton University Press,1948.