高超聲速巡航飛行器在線自適應反饋控制設計

李惠峰 李昭瑩

(北京航空航天大學 宇航學院,北京 100191)

高超聲速巡航飛行器在線自適應反饋控制設計

李惠峰 李昭瑩

(北京航空航天大學 宇航學院,北京 100191)

由于飛行器模型的強非線性,各種建模不確定性以及飛行環境的復雜性,高超聲速飛行器控制成為一個研究難點.針對某類具有參數不確定性的非線性系統,提出了一種反饋線性化與自適應估計相結合的方法,對非線性系統的輸入輸出動態應用反饋線性化處理以得到擬線性模型,并設計反饋控制律;對不確定參數采用自適應在線估計,利用 Lyapunov方法分析穩定性;針對選擇不同輸出的情況,對如何消除內動態進行了討論.為了驗證該方法的可行性,將其應用于某高超聲速飛行器巡航段縱向非線性模型,對速度和高度通道進行跟蹤控制仿真,由于飛行器和大氣環境存在建模不確定性,利用自適應控制對不確定參數進行在線估計.仿真結果顯示該方法能夠快速收斂,并且具有良好的在線自適應能力.

高超聲速飛行器;反饋線性化;自適應算法;穩定性;不確定性分析

高超聲速飛行器通常采用推進氣動耦合設計,雖然提高了推進效率,減小了氣動阻力,但是穩定性也大大降低,而在高速飛行時,飛行環境和飛行狀態變化復雜,所以飛行器對環境和模型的不確定性也十分敏感.在近些年的研究中,各種非線性控制理論諸如反饋線性化,自適應控制,神經網絡,滑模控制,反步法等,被應用于高超聲速飛行器的非線性控制,取得了較好的效果.文獻[1]里,針對一系列不確定性(比如推力失效,執行機構飽和,甚至控制失效等),對高超聲速巡航飛行器設計自適應控制器.文獻[2]基于一個飛行航跡角動力學存在非最小相位特性,推進和氣動之間存在強耦合的簡化模型,提出了一種兼備自適應性和魯棒性的設計方法.文獻[3]里綜合應用非線性動態逆和魯棒控制,提出了 38個評估系統性能的指標,用對這些指標的偏離和系統發生不穩定的概率來表征系統的魯棒性.文獻[4]提出了基于特征模型的自適應控制律設計方法,給出了飛行器的誤差特征模型,采用內-外環控制.文獻[5]應用非線性動態逆控制設計高超聲速飛行控制系統,并結合最優狀態調節器以獲得良好的控制性能.文獻[6]應用軌跡線性化方法,對空天飛行器進行控制器設計,并結合單隱層神經網絡提高了控制系統的自適應性.

從上述研究可看到,將幾種控制方法結合起來,充分利用各自的優勢,設計綜合控制器,是一種解決高超聲速飛行器飛行控制的有效途徑.由于反饋線性化能夠對高超聲速飛行器非線性模型進行有效的解耦,便于控制設計,而在處理不確定性(尤其是參數不確定性)方面,自適應控制又具有很大的優勢,因此將反饋線性化和自適應控制相結合,則除了解決非線性系統的控制問題,還能使設計的控制器具有良好的自適應性和魯棒性.

基于以上分析,本文首先提出了針對一類MIMO(Multip le-Input-Multiple-Output)非線性系統的控制設計方法,結合了反饋線性化和自適應控制,用輸入輸出反饋使非線性系統線性化,采用自適應估計來處理參數的不確定性,并用 Lyapunov方法論證穩定性;然后將該方法應用到某通用高超聲速飛行器縱向動力學模型,進行控制器設計,實現了對高度和速度的跟蹤控制,并對模型中存在的不確定參數進行了自適應估計.

1 問題描述

首先考慮一類 MIMO非線性系統:

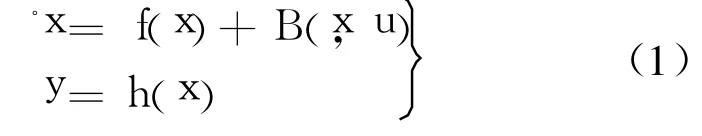
其中,x∈Rn為狀態向量;y∈Rm為輸出向量;u∈Rm為控制輸入;系統的輸入輸出維數相同,h是從 Rn→R的平滑函數.對輸出 y不斷微分,直到產生一個不為 0的控制輸入 u的分量系數,從而得到輸入輸出線性動態.

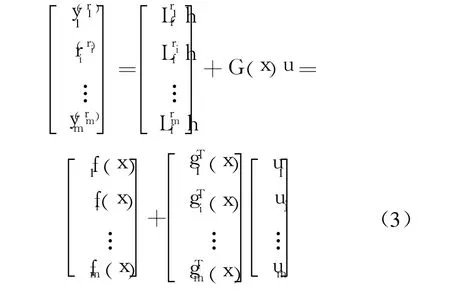
假設 gi(x)中存在不確定常值參數 θi,并可寫為

整理得到 G(x):

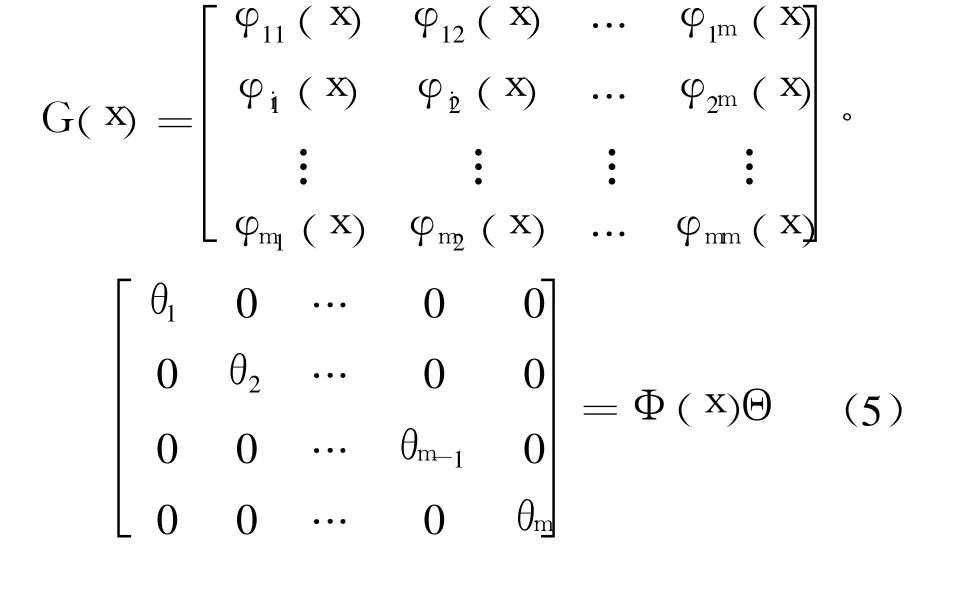
2 控制器設計和穩定性分析

2.1 反饋控制設計

控制的目標是使輸出跟蹤給定的輸入指令yd,設計反饋控制律如下(假定 G非奇異):

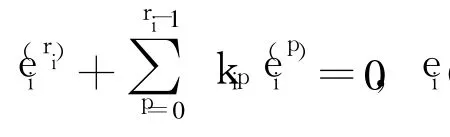
2.2 自適應控制器設計

i是對 ηi的在線估計.定義 Lyapunov函數如下:

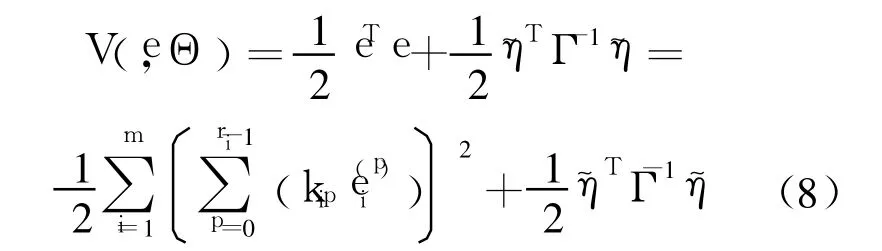
其中,γi是正常系數,且有

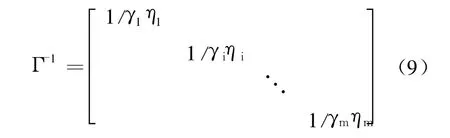
對 Lyapunov函數微分得

通過整理得到

又因為

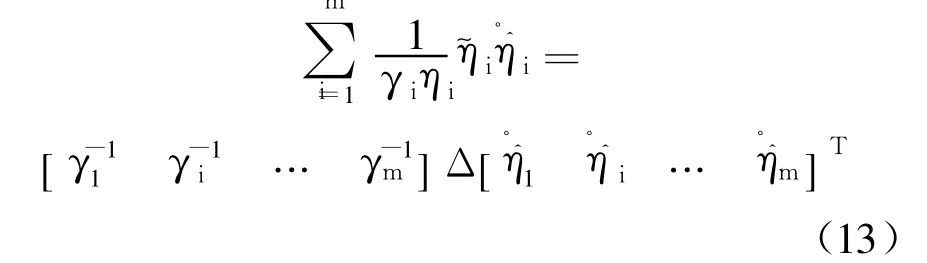
則對不確定參數進行估計的自適應律設計如下:

以 i=2,r1=2,r2=2為例,當反饋增益系數滿足時,

3 模型仿真

飛行器模型采用文獻[3]的巡航縱向模型,巡航速度為 15Ma,巡航高度為33km,控制目標是跟蹤速度和高度的階躍指令.

3.1 動力學模型

縱向動力學方程和二階發動機模型構成一個7階非線性系統.

按標稱巡航條件計算,氣動模型和推力模型如下:

控制輸入是升降舵偏轉角和節流閥:u=[βcδe]T.

通過在平衡點線性化,可以求得開環系統的特征根,對于高超聲速飛行器來說,采用上述的動力學方程模型,5個特征根將會包括一正一負的兩個短周期模態,分別對應俯仰角和攻角,兩個慢衰減的長周期模態,對應速度和航跡角,還有一個不穩定的高度模態.由于本文的氣動模型中,升阻力系數不包含升降舵偏轉角,沒有位于右半平面的零點,不存在非最小相位.

如果不引入二階發動機模型,單從動力學方程來看,系統的階數為 5,由于選擇的輸出是速度和高度,相對階為 7(3+4),因此存在內動態,在設計控制器的時候,還需要檢驗內動態是否能穩定,如果不能,則需要重新設計.而引入二階發動機模型后,就能避免出現內動態.

如果選擇輸出為 V和 γ,此時的相對階為6(3+3),為了構造一個 6階動力學系統,消除內動態,需要進行如下假設:①將重力加速度視為常值;②忽略離心力的影響.

在上述假設下,式(15)和式(16)中關于 r的項被去除,由于 h不再作為狀態量,式(17)也可省略,剩下的 4個動態方程和二階發動機模型一起構成 6階系統,從而滿足了消除內動態的需求.必須指出,這種簡化只是為了設計控制器方便,在仿真時,為了獲得相對準確的結果,應采用未簡化模型,以驗證控制器的穩定性和魯棒性.

3.2 控制器設計

經過反饋線性化后,可以將輸出動態寫為

其中

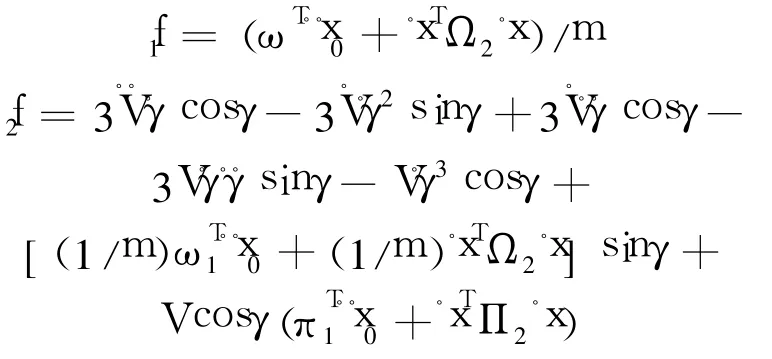
上述表達式的具體形式見文獻[3].從 G的具體表達式可以計算,在本文所討論的范圍內,當γ≠±π/2時,G非奇異.設計反饋控制器如下:

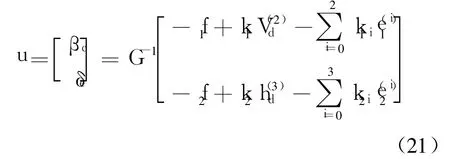
其中,Vd,hd是輸入指令;e1=V-Vd;e2=h-hd是跟蹤誤差.

3.3 在線自適應估計

由于增益矩陣中存在不確定參數,將其寫成如下形式,把不確定參數部分提取出來:

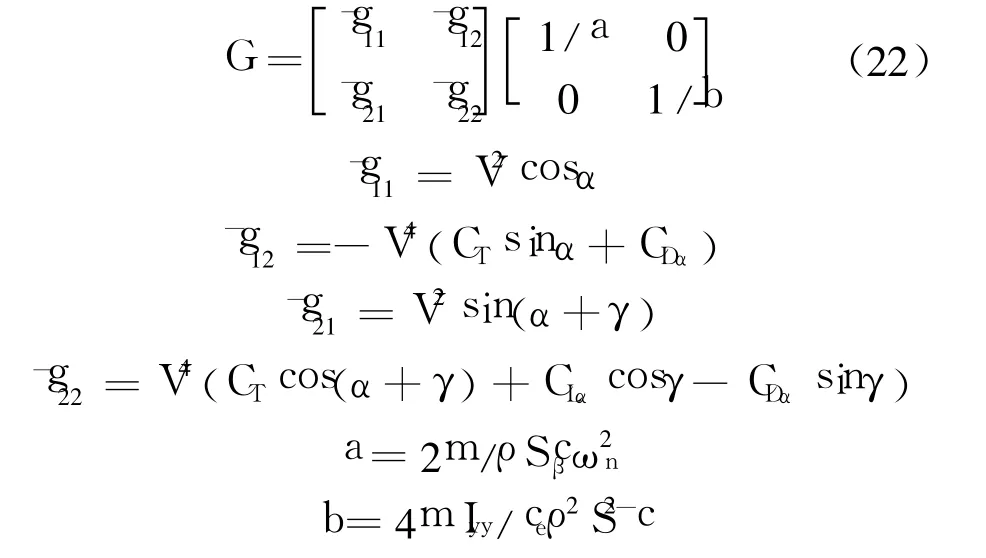
其中,a和 b是包含不確定常值參數 cβ,ρ,S,ce,c-,m的組合項.這些參數是難以準確測量的常值.a和 b的自適應律可設計為

4 仿真結果

首先驗證反饋控制律,在標稱模型下(無參數不確定性)分別對高度和速度的階躍指令進行跟蹤.圖 1是對 30m/s速度階躍指令的跟蹤響應曲線,速度迅速收斂到指令值,高度的變化非常小,相比巡航高度幾乎可以忽略不計;圖 2是對610m高度階躍指令的跟蹤響應曲線,同樣高度的收斂速度很快,而速度幾乎不變.控制變量也能夠快速穩定.

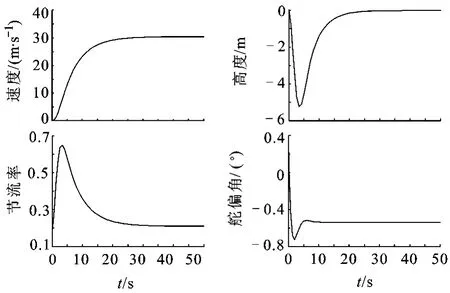
圖1 速度階躍指令響應(標稱模型)

在驗證自適應估計律時,a的額定值為8.289×106,b的額定值為 1.460×1013,通過計算發現當 m的不確定性為負,而 cβ,ρ,S,ce,c-的不確定性為正時,所有參數的組合項 a和 b的不確定性達到最大.取各參數的不確定性絕對值為2%,a和 b的真實值分別為 7.871×106和1.243×1013.在此條件下進行仿真,從圖 3和圖 4可以看到,自適應律使參數很快收斂到真實值,并且有效地降低了控制力(控制量節流閥變小),即為了實現同樣的跟蹤機動,引入自適應在線估計后能夠降低發動機的能量消耗.

圖4 高度階躍指令響應(參數不確定)

5 結 論

本文給出了一種結合反饋線性化和自適應估計來設計控制器的方法,實現了對階躍響應的跟蹤控制.在分析飛行器特性的基礎上,對利用反饋線性化解耦輸入輸出非線性動態進行了討論,給出了在選擇不同輸出時消除內動態的處理方法.對于參數不確定性,采用自適應在線估計,并給出了閉環系統的穩定條件.仿真結果顯示,在對參數引入一定范圍的不確定性下,控制系統仍能保證較好地完成控制任務,體現了較強的魯棒性.本文提出的控制策略設計思路清晰,能夠解決 MIMO非線性系統的控制跟蹤問題,并具有一定工程實用價值.

References)

[1]Gibson TE,Annaswamy A M.Adaptive control of hypersonic vehicles in the presence of thrust and actuator uncertainties[R].AIAA-2008-6961,2008

[2]Fiorentini L,Serrani A,Bolender M A,et al.Nonlinear robust/adaptive controller design for an air-breathing hypersonic vehicle model[R].AIAA-2007-6329,2007

[3]Wang Q,Stengel R F.Robust nonlinear control of a hypersonic aircraft[J].Journal of Guidance,Control and Dynamics,2000,23(4):577-585

[4]孟斌,吳宏鑫.高超聲速飛行器基于特征模型的自適應控制[C]//程代展,吳敏.第 26屆中國控制會議論文集.北京:北京航空航天大學出版社,2007:720-724 Meng Bin,Wu Hongxin.Adaptive control based on characteristic model for a hypersonic vehicle[C]//Chen Daizhan,Wu min.Proceeding of the 26th Chinese Control Conference.Beijing:Beijing University of Aeronautics and Astronautics,2007:720-724(in Chinese)

[5]劉燕斌,陸宇平.非線性動態逆控制在高超飛控系統中的應用[J].應用科學學報,2006,24(6):613-617 Liu Yanbin,Lu Yuping.Application of nonlinear dynam ic inversion control in flight control of hypersonic vehic le[J].Journal of Sciences,2006,24(6):613-617(in Chinese)

[6]朱亮,姜長生,陳海通,等.基于單隱層神經網絡的空天飛行器直接自適應軌跡線性化控制[J].宇航學報,2006,27(3):338-344 Zhu Liang,Jiang Changsheng,Chen Haitong,et al.Directed adaptive trajectory linearization control of aerospace vehicle using SHL NN[J].Journal of Astronautics,2006,27(3):338-344(in Chinese)

[7]Slotine JJE,LiW P.Applied nonlinear control[M].Upper Saddle River,New Jersey:Prentice Hall,1991

[8]Xu H J,Mirmirani M,Ioannou P A.Robust neural adaptive control of a hypersonic aircraft[R].AIAA-2003-5641,2003

(編 輯 :張 嶸)

Adaptive feedback control design for hypersonic cruise flight vehicle

Li Huifeng Li Zhaoying

(School of Astronautics,Beijing University of Aeronautics and Astronautics,Beijing 100191,China)

Because of strong nonlinear characteristics,modeling uncertainties and complicated flightenvironment,the control of hypersonic flight vehicle becomes a challenge.An approach which combines feedback linearization and adaptive control foramultiple-input-multiple-output(MIMO)nonlinearsystem with parameter uncertainty was proposed.Feedback linearization was used to obtain the linear input-output dynamics and a feedback controller was designed.The uncertain para meters were estimated online by an adaptive control law and the Lyapunov method was introduced to an alyse the close-loop system stability.For the conditions of choosing different outputs,a discussion was made on how to remove the inner dynamics to avoid unexpected unstable dynamics.A hypersonic cruise flight vehicle longitude model was used to testify the reliability of the proposed approach.In order to control altitude and velocity channel,a feedback controller with adaptive on line estimator was designed for the parameter uncertainties in vehicle model and atmosphere model.The simulation was operated to track the altitude and velocity step commands.Results show the controller has good tracking performance with rapid converge speed.

hypersonic vehicle;feedback linearization;adaptive algorithm;stability;uncertainty analysis

V 448.21

A

1001-5965(2010)11-1382-05

2010-01-19

李惠峰(1970-),女,陜西蒲城人,副教授,leehuifeng@buaa.edu.cn.