一道高一數(shù)學(xué)習(xí)題批改引發(fā)的思考

■江思容

一道高一數(shù)學(xué)習(xí)題批改引發(fā)的思考

■江思容

練習(xí)：已知集合A={1，2，}，B= {1,3}，且B≤A，求a的取值范圍。

解：因?yàn)锽≤A，所以a2-3a-1=3，配方得，即，所以有：，解得a=4或 -1。

這是高一學(xué)生學(xué)習(xí)集合后遇到的一個(gè)簡(jiǎn)單而典型的習(xí)題，翻看學(xué)生的作業(yè)，發(fā)現(xiàn)很多學(xué)生都是這樣解答的，教師也給了一個(gè)勾，批改錯(cuò)了嗎？沒有；解答合理嗎？顯然不合理；學(xué)生知道一元二次方程求根公式嗎？他們基本上都能正確寫出來。面對(duì)這種正確而不合理、知而不用的情形，教師該做些什么呢？

反思探究一：提高解題起點(diǎn)，調(diào)整認(rèn)知結(jié)構(gòu)

解題起點(diǎn)是指問題解決過程中思維的出發(fā)點(diǎn)，解題起點(diǎn)往往影響學(xué)生解題速度及解題長度，而解題起點(diǎn)的選擇與個(gè)體認(rèn)知結(jié)構(gòu)密切相關(guān)。在解題教學(xué)中，關(guān)注學(xué)生解題過程，從解題起點(diǎn)入手，將知識(shí)結(jié)構(gòu)內(nèi)化為學(xué)生的認(rèn)知結(jié)構(gòu)，有利于解題能力的提高。

從初中對(duì)一元二次方程的教學(xué)要求（浙教版）來看，學(xué)生要掌握一元二次方程的兩種解法：配方法和公式法。公式法是在配方法的基礎(chǔ)上推導(dǎo)出來的，是比配方法更高的概括和抽象，舍棄公式法選用配方法折射出學(xué)生沒有把公式法內(nèi)化為自己的知識(shí)，也就是還沒有把配方、開方、移項(xiàng)、求解等推導(dǎo)一元二次方程求根公式的過程壓縮成一個(gè)操作單元——求根公式，整合到自己的知識(shí)結(jié)構(gòu)中去，形成整體性的結(jié)構(gòu)化認(rèn)知，導(dǎo)致學(xué)生解一元二次方程的起點(diǎn)還是從配方開始。

用公式法解一元二次方程是一種技能，面對(duì)這種正確而不合理的解答，教師若置之不理，學(xué)生的解題技能是不會(huì)自動(dòng)獲取的。認(rèn)知心理學(xué)認(rèn)為熟練基本技能的獲得需要經(jīng)歷三個(gè)階段：①認(rèn)知階段，對(duì)這一技能包含的需要執(zhí)行的行為形成最初的陳述性編碼；②聯(lián)系階段，將陳述性知識(shí)轉(zhuǎn)化為程序性知識(shí)，構(gòu)成該程序各部分的產(chǎn)生式的連接，即條件與行為的一系列配對(duì)得以增強(qiáng)；③自動(dòng)化階段，整個(gè)程序得到進(jìn)一步的完善，使有關(guān)條件圖式與一連串的適當(dāng)反應(yīng)趨向自動(dòng)化。從學(xué)生的表現(xiàn)來看，還沒有對(duì)一元二次方程（圖式）產(chǎn)生自動(dòng)化的反應(yīng)（用求根公式），自動(dòng)化反應(yīng)的獲取需要一定的訓(xùn)練，類似的問題在教學(xué)中經(jīng)常出現(xiàn)，例如對(duì)數(shù)的運(yùn)算法則，學(xué)生記得很熟，用起來就錯(cuò)。

教學(xué)建議：針對(duì)學(xué)生“知而不用”或“一用就錯(cuò)”的現(xiàn)象，教師要抓住契機(jī)引導(dǎo)學(xué)生應(yīng)用所學(xué)知識(shí)解決問題，形成技能，并加強(qiáng)與相關(guān)知識(shí)的聯(lián)系，促進(jìn)知識(shí)、方法間的立體融合，將知識(shí)結(jié)構(gòu)內(nèi)化為學(xué)生的認(rèn)知結(jié)構(gòu)，促進(jìn)解題能力的提高。

反思探究二：理清解題起點(diǎn)，完善認(rèn)知結(jié)構(gòu)

荷蘭著名數(shù)學(xué)教育家弗賴登塔爾說過：“反思是數(shù)學(xué)思維活動(dòng)的核心和動(dòng)力。”當(dāng)今高考題型日趨模式化，以致很多教師在指導(dǎo)學(xué)生解答客觀題時(shí)過分強(qiáng)調(diào)答題技巧，追求答案的正確性，缺少對(duì)問題刨根問底的深究，這樣一來答案雖然正確，學(xué)生卻只知其“然”而不知其“所以然”。答案如同漂浮在水中的浮萍，找不到思維的支撐點(diǎn)，從而造成學(xué)生對(duì)問題的認(rèn)知不穩(wěn)定、不明晰、雜亂無章，不利于后續(xù)學(xué)習(xí)。反之，教師如果引導(dǎo)學(xué)生深究根源，找到思維的支撐點(diǎn)，就能有利于學(xué)生形成明晰、穩(wěn)定、有組織的認(rèn)知結(jié)構(gòu)，促進(jìn)學(xué)生學(xué)習(xí)的遷移，提升學(xué)生的解題能力。

例如2007年高考數(shù)學(xué)廣東卷：如圖（圖略）是某汽車維修公司的維修站點(diǎn)環(huán)形分布圖，公司在年初分配給A、B、C、D四個(gè)維修點(diǎn)某種配件各50個(gè)。在使用前發(fā)現(xiàn)須將A、B、C、D四個(gè)維修點(diǎn)的這批配件分別調(diào)整為40、45、54、61件，但調(diào)整只能在相鄰兩站點(diǎn)間進(jìn)行，那么要完成上述調(diào)整，最少的調(diào)動(dòng)件次(n個(gè)配件從一個(gè)維修點(diǎn)調(diào)動(dòng)到相鄰維修點(diǎn)的件次記為n)為()

A．15 B．16 C．17 D．18

通過觀察比較可得，A調(diào)10件到D，B調(diào)5件到C，C調(diào)1件到D，共調(diào)16件，選擇答案B．這樣雖然得到了正確的答案，卻缺少邏輯上的支撐，還存在明顯的漏洞：如何否定答案A？除了給出的調(diào)動(dòng)方案外，還有沒有其它的方案呢？這些問題若不能解決，學(xué)生對(duì)這個(gè)問題猶如霧里看花．要從根本上解決問題，教師不妨引導(dǎo)學(xué)生尋找問題的一般解法：

設(shè)A向B調(diào)配x1件，B向C調(diào)配x2件，C向D調(diào)配x3件，D向A調(diào)配x4件(xi＞0表示逆時(shí)針方向；xi＜0表示順時(shí)針方向；xi=0表示沒有調(diào)配)可得方程組如下：

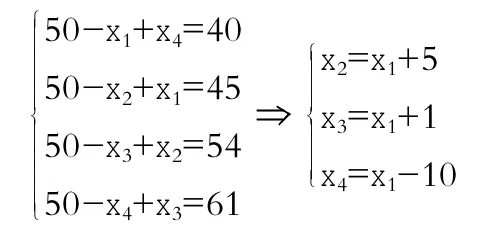
現(xiàn)在問題就轉(zhuǎn)化為求M=|x1|+|x2| +|x3|+|x4|=|x1|+|x1+5|+|x1+1|+|x1-10|下面對(duì)x1進(jìn)行分類討論，化為分段函數(shù)求最小值。

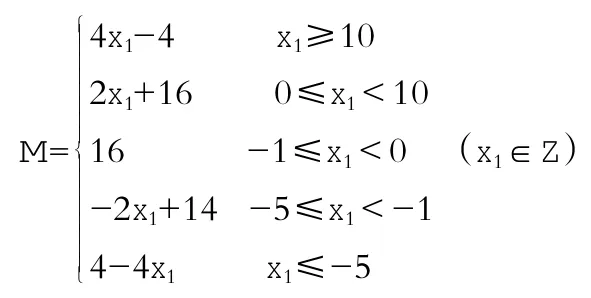
由分段函數(shù)的最小值可知，正確答案為B，有兩種調(diào)配方式，即分別取x1=0或-1所對(duì)應(yīng)的兩種調(diào)配方式。除分段函數(shù)求最小值外，還可以引導(dǎo)學(xué)生用絕對(duì)值不等式|a|+|b|≥|a±b|解決問題，然后總結(jié)規(guī)律。

教學(xué)建議：針對(duì)某些客觀題答案易得根據(jù)難尋的現(xiàn)象，教師可引導(dǎo)學(xué)生進(jìn)行“小題大做”，對(duì)“形異質(zhì)同”的問題歸類，挖掘問題的本質(zhì)，尋找思維的起點(diǎn)，完善學(xué)生的認(rèn)知結(jié)構(gòu)。

反思探究三：尋求合理解題方法，優(yōu)化認(rèn)知結(jié)構(gòu)

建構(gòu)主義學(xué)習(xí)論認(rèn)為：個(gè)體的學(xué)習(xí)不是在一片空白或完全相同的背景下進(jìn)行的，學(xué)習(xí)者已有的知識(shí)經(jīng)驗(yàn)、信念、個(gè)性、情感等都不同程度的參與其中。由于個(gè)體經(jīng)驗(yàn)的不同，學(xué)生對(duì)同一問題便會(huì)形成理解上的差異，表現(xiàn)在解題中就是對(duì)信息的表征、轉(zhuǎn)化不同，選擇的解題思路不同，自然就出現(xiàn)了同一問題，不同的解法。諸多解法中有繁有簡(jiǎn)，有通法有特法，盡管每種解法對(duì)解題者而言是“合適”的，然而過于繁雜的解法背后反應(yīng)的是解題者認(rèn)知結(jié)構(gòu)的不合理。數(shù)學(xué)學(xué)習(xí)過程是數(shù)學(xué)認(rèn)知結(jié)構(gòu)的發(fā)展變化過程，數(shù)學(xué)教學(xué)不僅要促進(jìn)學(xué)生認(rèn)知結(jié)構(gòu)的發(fā)展，還要幫助學(xué)生優(yōu)化其認(rèn)知結(jié)構(gòu)，學(xué)生解法的差異性正是教師可以利用的豐富資源。例如：

設(shè)函數(shù)f(x)=sin(2x+φ)(-π＜φ＜0)，y=f(x)圖像的一條對(duì)稱軸是直線x=。

(1)求φ的值；

(2)求函數(shù)y=f(x)的單調(diào)區(qū)間；

(3)畫出函數(shù)y=f(x)在區(qū)間［0，π］上的圖像。

學(xué)生在解答第一問時(shí)常用的方法有兩種：

解法1是基于對(duì)三角函數(shù)圖像軸對(duì)稱的考慮作出的解答，解法2是基于對(duì)一般函數(shù)圖像軸對(duì)稱作出的解答，還用到了特殊化的思想方法，解法2的包攝程度更高，具有更一般的意義及推廣價(jià)值，教師可以通過對(duì)兩種方法的比較分析，引導(dǎo)學(xué)生感悟兩種方法的區(qū)別與聯(lián)系，從而完善個(gè)體的認(rèn)知結(jié)構(gòu)。

教學(xué)建議：在解題中表現(xiàn)出來的個(gè)體差異是一筆寶貴的財(cái)富，教師可以選擇典型問題、典型解法進(jìn)行分析，促進(jìn)學(xué)生之間思想方法的交流，優(yōu)化學(xué)生的認(rèn)知結(jié)構(gòu)。

作業(yè)批改是教學(xué)的重要環(huán)節(jié)，教師不僅要當(dāng)好裁判員，還要當(dāng)好教練員，通過作業(yè)批改，洞察學(xué)生學(xué)習(xí)中存在的問題，采取相應(yīng)措施，幫助學(xué)生優(yōu)化知識(shí)、方法的組合方式，完善認(rèn)知結(jié)構(gòu)，促進(jìn)學(xué)生數(shù)學(xué)認(rèn)知的發(fā)展。

（作者單位：武漢市洪山區(qū)教育科學(xué)研究培訓(xùn)中心）

責(zé)任編輯 王愛民