均勻分布和密度與正態密度的逼近速度及應用

李瑞閣，萬冰蓉，許洪范

(1.南陽理工學院應用數學系,河南 南陽 473006；2.南昌工程學院 理學系,南昌 330099)

1 IID均勻分布和密度函數一般公式及期望方差公式

（1）設 X1，X2，…，Xniid～U（0，1）當 x∈[k，k+1]時，

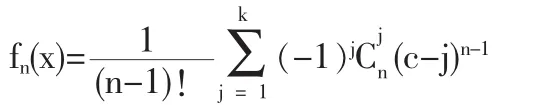
對于其他x上式等于0。

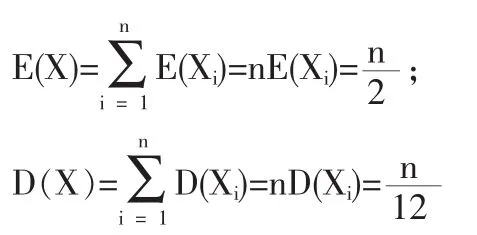
2 IID均勻分布和密度與正態密度擬合圖,兩者差的絕對值圖，絕對值最大值表及趨勢圖

（1）在數學上，數形結合的思想，不僅能從直覺上給我們以啟示,常常能借助變化的趨勢，發現事物的客觀規律性。

用正態分布去擬合fn(x)主要有兩種方法：

②用曲線擬合最小二乘法，用數學軟件編程實現:如n=5,N(2.5,0.4489)。

這里用第二種方法。用Matlab分別畫出當n=2，3，4，5時的和分布密度圖及相應的正態分布圖 （見圖1，圖2，圖 3，圖 4）。

③用Matlab分別畫出當n=2，3，4，5時的相應和分布密度與正態密度的差的絕對值在 [0，3]，[0，5]，[0，6]，[0，8]內，依次取 100，100，150，200 個等分點的差值圖（見圖 5，圖 6，圖 7，圖 8），并計算出對區間盡可能細分情況下，和密度函數與相應正態分布函數的差的絕對值的最大值。

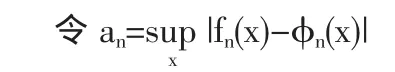
其中，當 x∈[k,k+1]時，

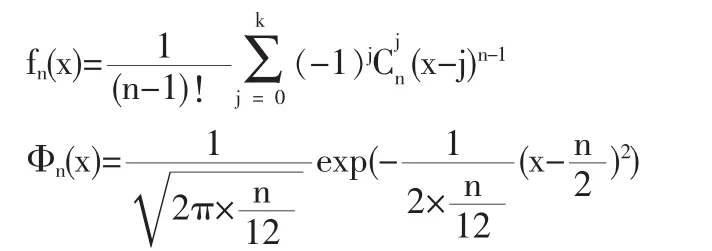
當 n=2,3,…，31 時，an在[0,n+2]上的最大值（見表 1），并畫出前24個值對應的差的絕對值最大值趨勢圖（見圖9）。

3 正態分布擬合結論

(1)由圖1，圖2，圖3，圖4可觀察到:隨著服從均勻分布的多個獨立隨機變量個數n不斷增大，這些變量和的密度函數與對應的正態分布的擬合程度愈來愈好。

(2)由圖5，圖6，圖7，圖8觀察發現,和密度函數與正態分布密度函數差的絕對值最大值，分別在和密度函數不為零的區間[0，2]，[0，3]，[0，4]，[0，5]上達到，且從右端點開始，在擴大的區間[0，3]，[0，5]，[0，6]，[0，8]上，隨著自變量的增大，差的絕對值越來越小，這個趨勢可隨區間的繼續增大而無限趨近于0；同理，由正態分布的對稱性，在左端點以外，和密度函數為零區間上，可以預見，隨著自變量的減小，差的絕對值越來越小,無限趨近于0。

(3)由圖9，表1很清楚的看到隨著變量個數的增加，分段函數在放大區間上，和密度函數與正態密度函數的差絕對值的最大值，隨著n增大，逐漸減小，越來越趨近于零，分布密度與正態分布密度隨著n的增大，逼近速度越來越快。

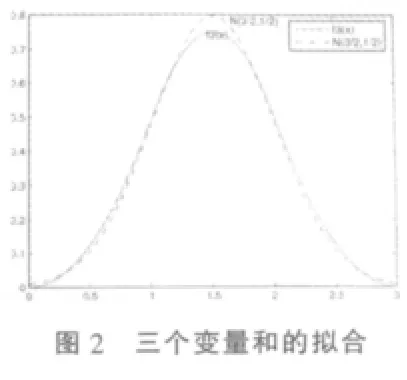
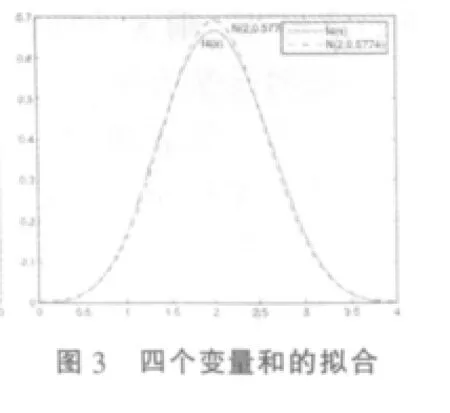
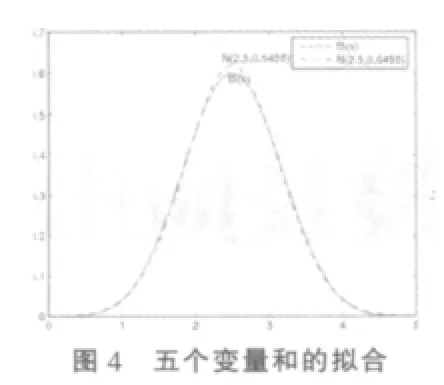
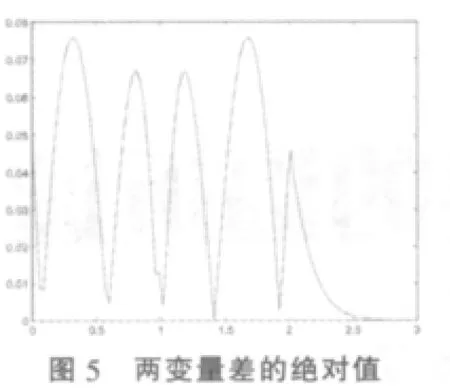
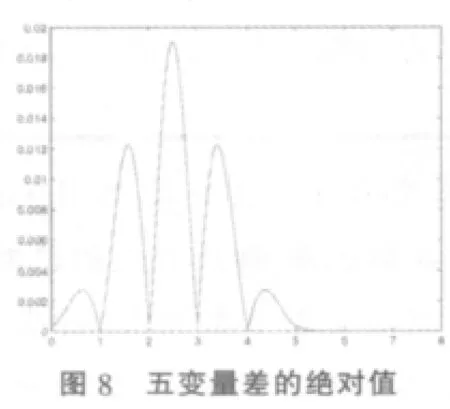
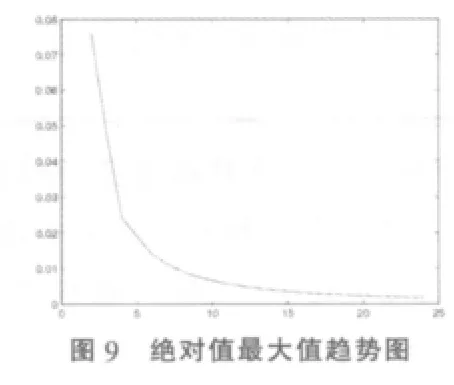
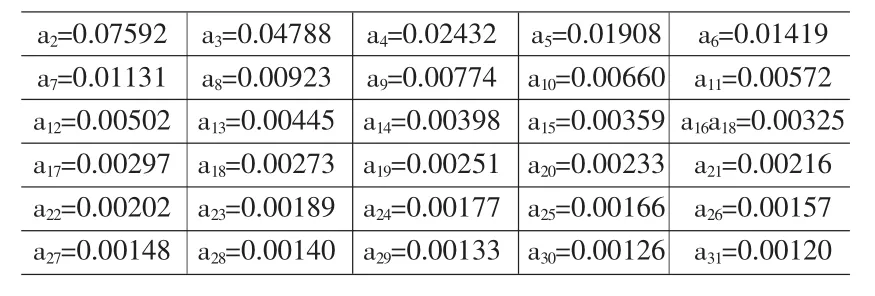
表1 差絕對值的最大值數據

(4)利用Matlab考察和密度函數與正態分布密度函數差絕對值的最大值an隨n的變化趨勢。利用逐步回歸法，并根據常識確定an與及n-1的關系為

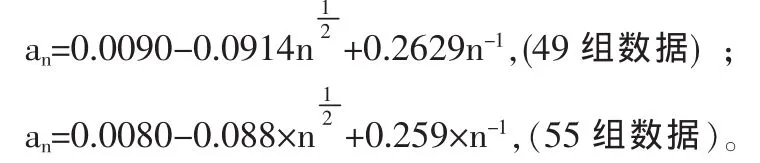
復相關系數R為0.997，且以此方程預測an的值與實際值差趨近于0，因此認為該方程適合統計學理論Edgeworth展開理論。不僅有統計學意義，且有實際意義。當n→∞，an→0。

綜上，當服從均勻分布的獨立隨機變量個數很多時，均勻分布和分布無限逼近正態分布，它們和的分布可近似看成正態分布，這個結論符合中心極限定理。

4 和分布密度逼近正態分布密度函數的結論,用于正態隨機數生成

由于上述的特性以及下面理論上的原因，均勻分布U(0,1)在隨機模擬中起著特殊的作用。通過產生大量相互獨立的U(0,1)的隨機數，經過一些相應的變換可得到其他形式(正態分布、指數分布、Gamma分布等)的隨機數。

命題1:若隨機變量Y有嚴格單調上升連續的分布函數F(y)，X=F(Y)，則 X 為隨機變量。

證明:∵Y為隨機變量，

∴?一維β集，及σ代數F,使得 Y-1(-∞,w)∈F

∴對于一維 β 集(-∞,η)有

X-1((-∞,η))=(F(Y))-1(-∞,η)=Y-1(F-1(-∞,η))∈F (F-1(-∞,η)∈β)

∴X為隨機變量。

命題2 若隨機變量Y有嚴格單調上升連續的分布函數 F(y)，X=F(Y)則 X～U（0，1）， 反 之 ,若 Z～U（0，1）,F為任一嚴格單調上升連續的分布函數，F-1為它的反函數，則 W=F-1（Z）的分布函數為 F（w）。

表2 均勻分布隨機數

證明:對任一 0≤x≤1有

P(X≤x)=P(F(Y)≤x)=P(Y≤F-1(x))=F(F-1(x))=x

∴X～U(0,1)

反之，若Z～(0，1)，F為任一嚴格單調上升連續的分布函數，F-1為它的反函數，則W=F-1(Z)的分布函數為F(w)。

P(W≤w)=P(F-1(Z)≤w)=P(Z≤F(w))=F(w)

∴W的分布函數為F(w)。

利用上述關系，可以產生各種常見分布F(x)的隨機數。所謂某個分布F(x)的隨機數，是指從分布F(x)的總體中隨機地抽取一個大樣本的數值，借助適當運算得到。

用機器來模擬抽樣比實際抽樣不僅成本低，而且可以有效地防止一些不必要的干擾，從而廣泛地應用于各個領域中。

5 產生正態隨機數的方法

在(0，1)中產生n個均勻分布的隨機數X1,X2,…，Xn即設X1,X2,…，Xn獨立同分布，由于

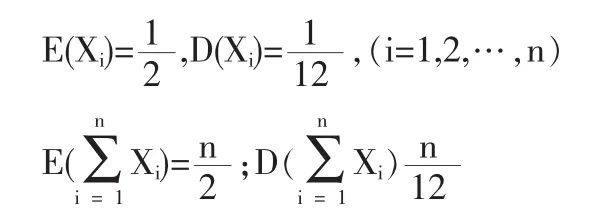
由中心極限定理知

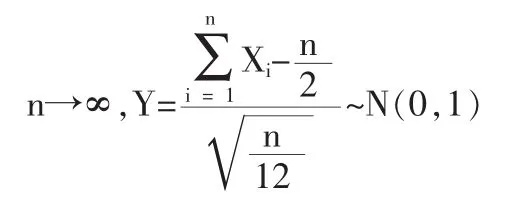
故Y為所求的N（0，1）的隨機數。

例：今用Matlab軟件,取得的均勻分布隨機數（見表2）。進而計算正態隨機數為

[1]李瑞閣,黃堯.服從均勻分布的多個獨立隨機變量和的密度函數公式[J].南陽師范學院學報,2007,(6)3.

[2]梁之舜,鄧集賢,楊維權等.中山大學數學系.概率論及數理統計[M].北京:高等教育出版社,2003.

[3]沈鴻.一類U統計量函數的Edgeworth展開[J].中國計量學院學報,2005,16(2).

[4]高惠璇.統計計算[M].北京:北京大學出版社,2005.[5]方開泰等.統計分布[M].北京:科學出版社,1987.