一類具有球面葉層結構的二次廣義Hamilton系統的分支結構
陳 強, 趙曉華
(浙江師范大學 數理與信息工程學院,浙江 金華 321004)
0 引 言
隨著人類認識、改造和利用自然能力的不斷提高以及實際應用的需要,經常需處理大量非線性問題.Hamilton系統是非線性科學研究中的一個重要領域,它的產生與發展具有深刻的實際背景[1].經典的Hamilton系統都是在偶數維相空間上定義的,這種結構雖然具有很好的性質,也有豐富的研究成果和實際應用[2],但也限制了其應用范圍.為了使Hamilton系統的觀點和方法能應用于實際研究中廣泛存在的奇數維系統(一個最經典的例子是自由剛體定點轉動的Euler方程,其相空間是3維的,由3個角動量軸構成),人們對經典的Hamilton系統進行了擴展,從而提出了廣義Hamilton系統的概念[3].廣義Hamilton系統是通過廣義Poisson括號定義的,而廣義Poisson括號是去掉非退化條件限制的Poisson括號.因此,用廣義Hamilton系統可以研究奇數階的非線性系統.廣義Hamilton系統的Poisson流形(具有廣義Poisson括號結構的流形)表示法是一種十分方便、有用的表示法.所以,Hamilton系統已由經典的(偶數維)形式推廣為廣義形式(任意維).
廣義Hamilton系統作為經典Hamilton系統的推廣,可以作為描述包括奇數維系統在內的更加廣泛的非線性動力學問題的模型,在機械工程、光學、分子動力學等領域中都有很多的應用,其中很大的一類是具有球面葉層結構的廣義Hamilton系統[2,4-5].在許多實際模型中,這種具有球面葉層結構的Hamilton系統模型,其Hamilton函數常以二次函數的形式居多.文獻[6]已證明,對它的研究可以歸結為對以下5類Hamilton函數所對應的廣義Hamilton系統的研究:
1)H=w;
迄今為止,對前4種情況,相應的廣義Hamilton系統在球面葉層上的平衡點分叉及其全局相圖已被完全研究清楚[7-9].但對Hamilton函數中含4個參數的第5種情況,正如文獻[10]指出的,其對應的廣義Hamilton系統在球面葉層上的分叉及相圖還未見相關報道.
基于此,筆者利用微分方程定性理論與動力系統分叉理論(特別是Hamilton系統相圖分析技巧)研究了第5類Hamilton函數在λ=1時所對應的具有球面葉層的廣義Hamilton系統,仔細分析了平衡點分叉及穩定性,獲得了完整的全局相圖分類.
1 平衡點分叉及穩定性分析

(1)
此時的Casimir函數為G(u,v,w)?u2+v2+w2,其水平集是以(0,0,0)為中心的球面,記為ML={(u,v,w)|u2+v2+w2=L2}.由于C≠0,故可將式(1)改寫為
(2)
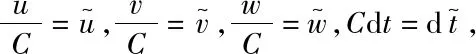
(3)

由上述討論可知,只需對系統(1)在C=1時的參數進行討論即可,即
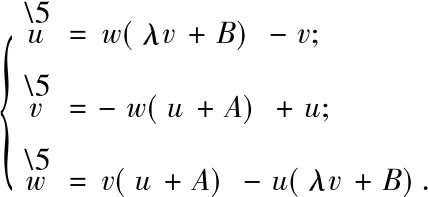
(4)
為了進一步簡化研究其相圖的性質,作如下對稱變換:
(u,A)→(-u,-A);(v,B)→(-v,-B).
顯然,系統(1)在此變換下保持H不變,說明只需要對參數A≥0且B≥0的情況進行討論即可.
下面考慮系統(4)的平衡點個數及其穩定性隨參數變化的分叉性質.由系統(4)的相空間具有葉層結構的性質以及Casimir函數可知,其平衡點由以下方程組確定:
(5)
經過化簡可得平衡點(u,v,w)的分量v滿足分叉方程
F(v)=A2v2(λv+B)2+v2[(λ-1)v+B]2+
(v2-L2)[(λ-1)v+B]2(λv+B)2.
(6)
與方程F(v)=0的根ve對應,可以得到系統(4)的平衡點q=(ue,ve,we),其中
(7)
為了弄清系統(4)平衡點q的穩定性,給出其Jacobi矩陣
其相應的特征方程為
|τI-Ja|=Bτ+τ3=0.
其中
B=ue(ve(λ-1)(-1-λ+2weλ)+
B(-we-λ+2weλ))+A(Bwe(λ-1)+
ve(1+we(λ-2)λ))+(-1-A2-
Bve(2λ-1)).
(8)
由此特征方程易知其3個根為:
根據微分定性理論[11]和廣義Hamilton系統的性質可得命題1.
命題1平衡點類型與B的關系如下:
1)當B<0時,τ2,3為一對實數根,此時系統(4)的平衡點q=(ue,ve,we)為鞍點;
2)當B=0時,τ1,2,3為三重零根,此時系統(4)的平衡點q=(ue,ve,we)為尖點;
3)當B>0時,τ2,3為一對純虛根,此時系統(4)的平衡點q=(ue,ve,we)為中心.
根據前面的討論可知,系統(4)的平衡點q=(ue,ve,we)是由分叉方程(6)的解決定,而B的符號也是由分叉方程(6)的解決定.因此,接下來就討論分叉方程的零根的個數隨參數變化的分布情況.
考慮到分叉方程的復雜性, 筆者僅對λ=1的情形進行討論.
當λ=1時,其特征方程為

定理1
1)當ve>v*時,B1>0,此時系統(4)的平衡點q=(ue,ve,we)為穩定平衡點,并且是個中心;
2)當ve=v*時,B1=0,此時系統(4)的平衡點q=(ue,ve,we)為穩定平衡點,并且是個尖點;
3)當ve 接下來利用定理1判別在不同參數條件下系統(4)的平衡點個數和類型. 當λ=1時,此時關于v的多項式函數變為 F(v)=A2v2(v+B)2+v2B2+ (v2-L2)B2(v+B)2= (A+B)2v2(v+B)2+v2B2- L2B2(v+B)2. 則可分析得到: 1)當0 ①當0 ②當1≤L 2)當L=M時,由多項式根的分布可知f1(v)與f2(v)有1個切點和2個交點,多項式函數f1(v)與f2(v)的圖像如圖3所示.因為f1(v)=f2(v)有3個根v=v(1),v(2),v(3)(切點),v(1),v(2)>-B>v*,所以2個為穩定平衡點.當v=v(3)時,B1=0,所以也為穩定平衡點(尖點).即此時有3個平衡點e1,e2和e3,且都是穩定平衡點,并且是2個平衡點e1,e2為中心、1個平衡點e3為尖點. 圖1 0 圖3 L=M時f1(v)與f2(v)交點及根的分布圖 圖4 L>M時f1(v)與f2(v)交點及根的分布圖 3)當L>M時,由多項式根的分布可知f1(v)與f2(v)有且僅有4個交點,即此時有4個平衡點,多項式函數f1(v)與f2(v)的圖像如圖4所示.設f1(v)=f2(v)的4個根為v(1),v(2),v(3),v(4).由函數f1(v)與f2(v)圖像可知,v(4) 有了前面的平衡點分叉及穩定性分析,就可以研究系統(4)的球面葉層上的全局相圖.由前面的參數分析可得: 1)當 0 如圖5(a)所示,e1和e2為系統(4)的2個穩定平衡點,且都為中心. 2)當L=M時,系統(4)的相圖為2個中心、1個尖點. 如圖5(b)所示,e1,e2和e3為系統(4)的穩定平衡點,e1,e2為中心,e3為尖點. 3)當L>M時,系統(4)的相圖為3個中心、1個鞍點. 如圖5(c)所示,e1,e2和e3為系統(4)的穩定平衡點,e4為系統(4)的不穩定平衡點,e1,e2和e3為中心,e4為鞍點. (a)2個中心 (b)2個中心1個尖點 (c)3個中心1個鞍點 利用微分方程定性理論與動力系統分叉理論研究了二次Hamilton函數在λ=1時對應的具有球面葉層結構的廣義Hamilton系統,仔細分析了平衡點分叉及穩定性性質,獲得了對應的全局相圖分類.但是,對此類二次廣義Hamilton系統更一般的情況(λ≠1)還有待于進一步研究. 參考文獻: [1]Arnold V I.Dynamical systems Ⅲ[M].Berlin:Springer-Verlag,1988. [2]Arnold V I.Mathematical methods of classical mechanics[M].2nd ed.New York:Springer-Verlag,1989. [3]李繼彬,趙曉華,劉正榮.廣義哈密頓系統理論及應用[M].北京:科學出版社,2007. [4]Pyshchev A P.Classical approach to effective rotational energy and bifurcation in rotational dynamics ofH2Xmolecules[J].Physical Review A,2003,68(4):1-10. [5]Zhilinski B I.Symmetry invariants and topology in molecular models[J].Physics Reports,2001,341(1/2/3/4/5/6):85-171. [6]Frauendiener J.Quadratic Hamiltonians on the unit sphere[J].Mech Res Commun,1995,22(4):313-317. [7]Lanchares V,Elipe A.Bifurcations in biparametric quadratic potentials[J].Chaos,1995,5(2):367-373. [8]Lanchares V,Elipe A.Bifurcations in biparametric quadratic potentials Ⅱ[J].Chaos,1995,5(3):531-535. [9]Lanchares V,Inarrea M,Salas J P,et al.Surfaces of bifurcation in a triparametric quadratic Hamiltonian[J].Physical Review E,1995,52(5):5540-5548. [10]Elipe A,Lanchares V.Exact solution of a triaxial gyrostat with one rotor[J].Celest Mech Dyn Astr,2008,101(1/2):49-68. [11]張芷芬,丁同仁,黃文灶,等.微分方程定性理論[M].北京:科學出版社,1985.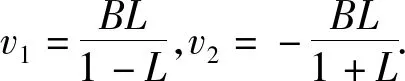

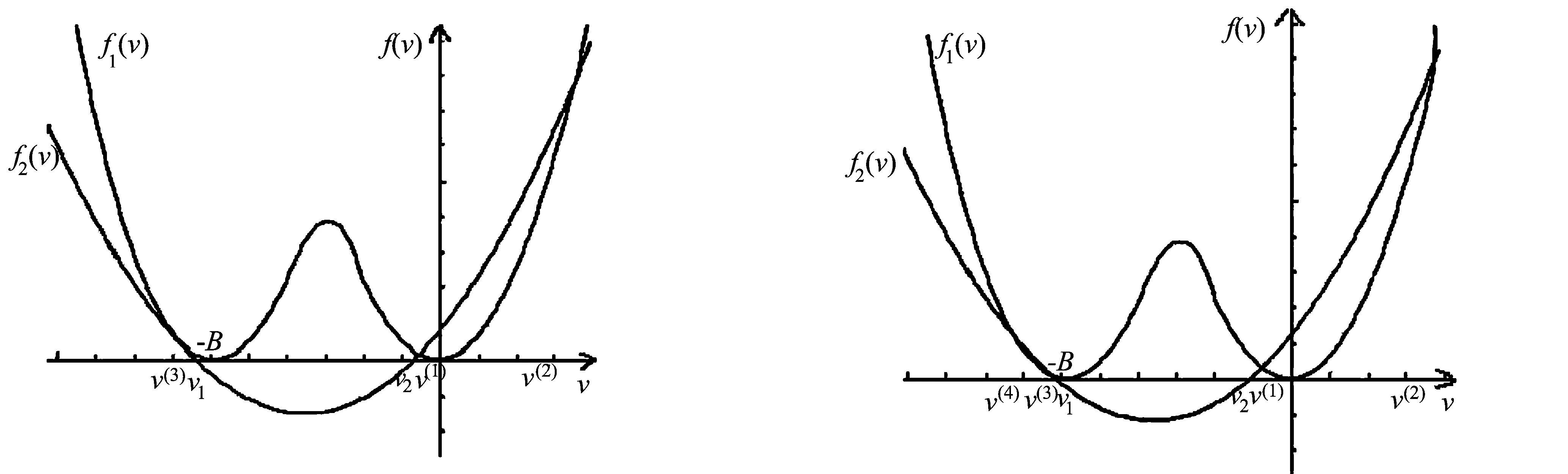
2 球面葉層上的全局相圖

3 小 結

