基于正態模糊化方法的在機測量系統性能模糊綜合評判

儲曉承 葉文華 俞 暉 管志鋼

1．南京航空航天大學，南京，210016 2．南通科技投資集團有限公司，南通，226001

0 引言

在機測量是工件加工后不卸下，將刀具換成測頭，在測量程序控制下采集工件表面上的測點坐標值，由測量軟件計算出工件的加工誤差。與坐標測量機的測量相比，在機測量具有效率高、無二次定位誤差等優點，已成為目前零件加工尺寸測量領域關注的熱點。

迄今為止，國內外學者對在機測量已經做了不少研究。Cho等［1］研究了基于 CAD／CAM／CAI集成的在機測量路徑規劃；Ki m等［2］研究了在機測量中裝夾誤差的補償技術；Ki m等［3］提出了一種提高在機測量精度的方法；文獻［4－5］研究了在機測量誤差的軟件補償技術；高峰等［6］研究了在數控成形砂輪磨齒機上實現在機測量的方法。綜合文獻資料的研究成果可知，目前對在機測量領域的研究主要涉及測量規劃、測量誤差計算分析及補償技術，而對測量系統整體性能的評價分析鮮見報道。事實上，在機測量系統是一個由數控機床、探測系統和測量軟件系統組成的總系統，影響其測量結果的因素眾多。這些因素不僅給在機測量系統的性能評價帶來困難，也給測量誤差的溯源帶來了困難，影響了在機測量系統的推廣應用。因此，有必要從系統的角度對在機測量系統性能進行綜合評價，為系統進行適用性分析、誤差溯源以及系統改進提供科學依據。

鑒于在機測量各子系統與整體之間的層次關系以及子系統試驗數據的統計特點，本文根據多層次模糊綜合評判理論建立在機測量系統綜合評價模型，引入正態模糊化方法處理試驗數據，建立模糊評價矩陣，合理地確定各指標權重系數，求解各級模糊子集的隸屬程度，實現在機測量系統的性能評價。

1 多層系統模糊綜合評判方法

模糊綜合評判是一種基于模糊數學隸屬度理論的綜合評價方法，即用模糊數學對受到多種因素制約的事物或對象作出一個總體的評價。設因素集 X ＝ ｛x1，x2，…，xn｝，評價集V ＝ ｛v1，v2，…，vm｝，從因素到評價的模糊關系?R表示對各個單因素xi作各種評價的可能性。設?R＝［rij］n×m，則rij為因素xi對評價vj的隸屬度。?A是一種權重分配，?A＝（a1，a2，…，an），它表示各因素在評價中的重要性。

根據模糊變換的原理，模糊綜合評判就是作如下模糊變換［7］：

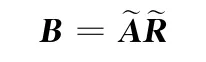
即

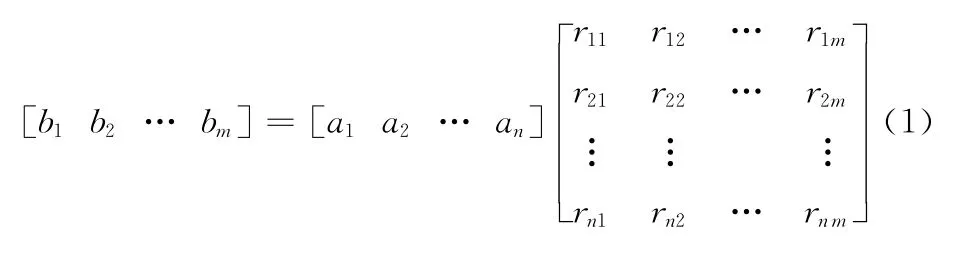
上述模糊變換過程為簡單（或單層）模糊綜合評判，適用于因素較少的簡單系統。當評判問題中考慮的因素較多時，簡單模糊綜合評判方法會產生一系列問題，如權重系數決定較難、各因素權重分配過小、合成運算中的信息丟失等。這些問題會導致評判結果分辨率很差，甚至得不到評判結果。

與簡單系統相比，復雜系統由于評判過程中考慮的因素較多，無法直接采用單層綜合評判的方法，但可以先將系統分層再逐層逆推評價，使復雜系統模糊評價問題轉化為簡單模糊評價問題。即首先將因素集按屬性或者按子系統分類，構成具有層次結構的系統評價體系；然后從最底層開始，在每一層內部進行獨立的簡單模糊綜合評判，其評判結果作為因素集用于上一層次的評判計算，以此逐層逆推直至獲得最高層（總系統）的評價結果。

圖1給出了二層系統模糊評判模型，圖中?Rk、?Ak、?Bk（k＝1，2，…，s）分別為各子系統評價矩陣、權重向量和評價結果向量。

2 在機測量系統綜合評價模型

2．1 在機測量系統評價指標體系

在機測量系統一般由三個部分組成：數控機床、測頭系統和測量軟件。系統的性能是各部分共同作用的結果，且每個子系統的性能由獨立的指標體系來評價。圖2所示為一個完整的加工中心在機測量系統。由于在機測量系統是具有二層結構的評價體系，故可以采用多層系統模糊評判的方法進行評價。

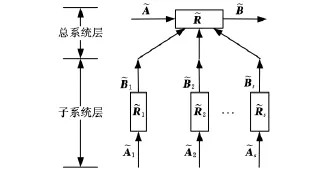
圖1 二層系統模糊評判模型

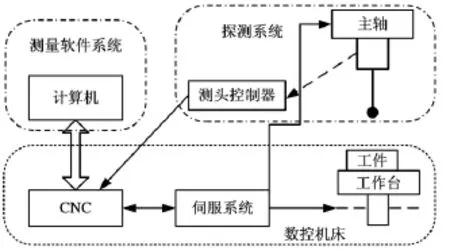
圖2 在機測量系統結構圖

從測量原理上說，在機測量系統直接測到的是被測工件上一些特征點的坐標值，需要通過軟件運算才能獲得被測元素的值。被測元素的測量精度主要與下列因素有關［8］：

（1）數控機床精度。該精度主要包括機床線性軸位置精度、旋轉軸位置精度、機床幾何精度以及幾何精度穩定性。其中，位置精度一般由定位精度、重復定位精度、反向定位差值等項目評定；幾何精度包括位置偏差、垂直度偏差、直線度偏差、角擺偏差等；幾何精度穩定性反映機床精度的變化情況。

（2）測量軟件算法精度。因為被測幾何元素不是理想元素，在數據處理中總是用以近似的理想元素替代它，這一過程叫做擬合算法計算。測量系統的算法性能主要通過直線、平面、圓、圓柱和球等基本元素的擬合精度來評價。

（3）測頭系統精度。該精度包括測針復位精度、預行程誤差、測針位置精度等要素。復位精度表示測頭每次在同一點觸發的性能；預行程是指從探針接觸工件到測頭發出觸發信號這段時間內測頭探針的變形量；測針位置精度反映測針與測頭中心軸線的偏離程度。

除了以上系統固有的影響因素外，工件的測量精度還與工件形狀誤差、環境因素和采樣策略有關，但這些均屬于外部因素，與本文討論的在機測量系統性能無關。由此，筆者提出的在機測量系統性能評價指標體系如圖3所示。

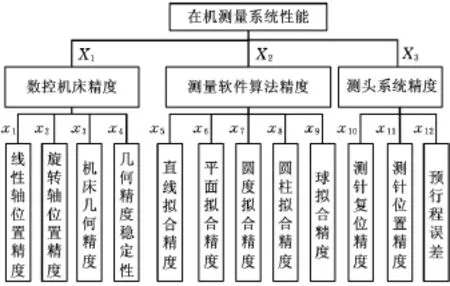
圖3 在機測量系統性能指標體系

2．2 在機測量系統各指標數據確定

為了使各指標性能值符合客觀實際，需要對各指標進行檢驗。在機測量系統各指標性能檢驗數據的獲取方法如下：

機床性能要求按國家標準［9］進行檢測，檢測數據可由機床廠家提供，通過比較允差值與實測值判斷檢測項目是否合格。測量軟件的算法測試可以參考坐標測量機軟件評定標準（GB／T16857．6）規定的評定方法［10］，該標準規定了軟件算法性能值p和最大允許誤差pMPE，具體評定結果可由軟件開發商提供。機床測頭參數由測頭廠家提供，評價機床測頭的精度可以將其參數與坐標測量專用測頭比較，根據比較的結果判斷測頭的精度水平。

鑒于各子系統指標檢測數據的表達方式不同，需要對其作概率化處理，即將檢測數據約束至0和1之間，越接近1說明精度越高，越接近0說明精度越低。對各子系統檢測數據的處理可采用表1所示的方法。

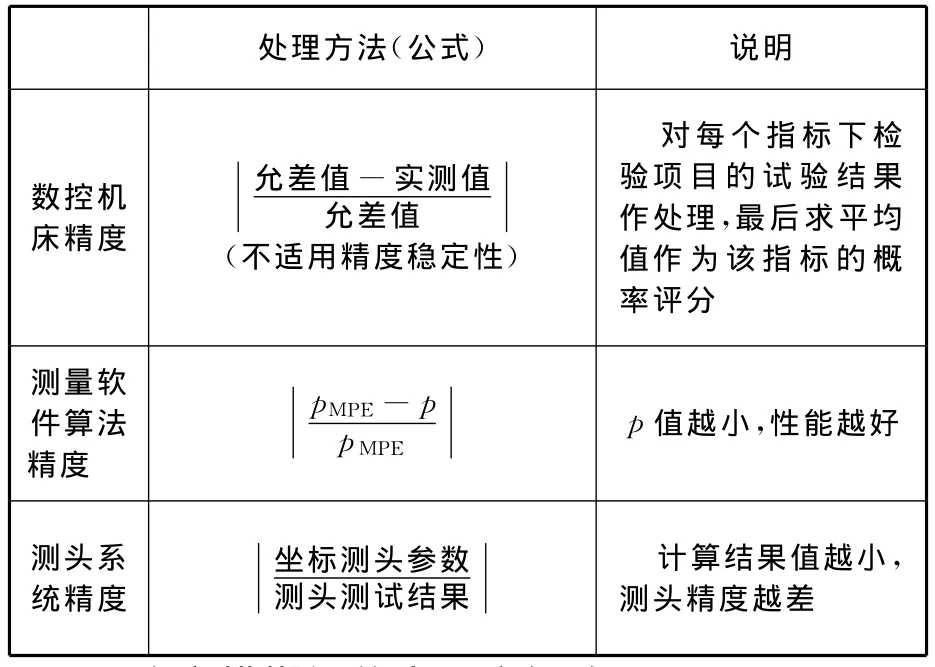
表1 檢測結果概率化處理方法

2．3 確定模糊評價隸屬度矩陣

在機測量指標以定量指標為主，且各子系統均屬于高精度產品，其性能一般通過精度的高低來反映，因此這里采用精度儲備量等級來評價各指標性能。將在機測量系統各指標性能評價分為5個等級，即其模糊論域為（五級、四級、三級、二級、一級）。精度儲備量五級最高，一級最低。

各指標評價等級的隸屬度μj（j＝1，2，…，5）可用專家打分法或者分布函數計算法來確定。專家打分法不太好操作，且評價數據的客觀性和準確性會受主觀因素影響，因此，對于具有精確指標的在機測量系統的評價，采用分布函數法對精確量進行模糊化處理是更合理的［11］。根據表1中的方法獲取各性能指標的概率型評價數據后，可以采用正態模糊化方法處理，得到模糊評價隸屬度矩陣。

設u（0≤u≤1）為精確量化的評價數據，σ為正態分布方差，則其正態分布函數為

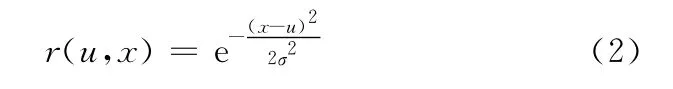
模糊論域（五級、四級、三級、二級、一級）在［0，1］區 間 中 對 應 的 區 間 分 別 為 （0．8，1．0］，（0．6，0．8］，（0．4，0．6］，（0．2，0．4］，［0，0．2］，其隸屬度設為μ1、μ2、μ3、μ4、μ5。根據分布函數和模糊量對應的區間，采用分段積分可得各模糊量的隸屬度。但是已有研究表明：這種標準的正態模糊化方法在當u接近0或者1的時候，其計算存在邊緣非單調的缺陷［11］。為此，對式（2）進行改進，改進后的正態模糊化方法數學表達如下：

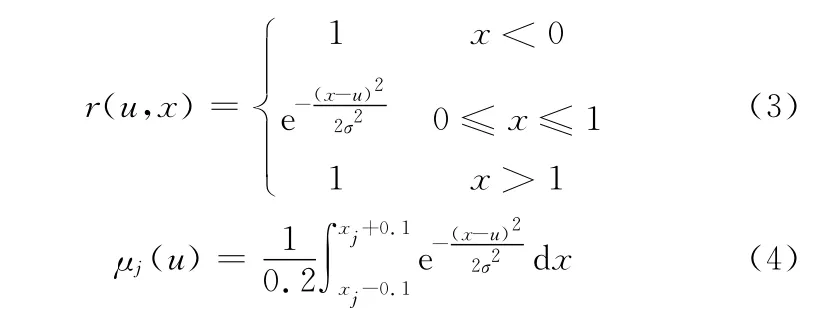
其中，x1＝0．9，x2＝0．7，x3＝0．5，x4＝0．3，x5＝0．1。規定當u＞0．9時，x1＝u；當u＜0．1時，x5＝u。

對指標體系中的每一個指標獲取概率型評價值ui，根據式（3）和式（4）分別計算各指標的模糊評價隸屬度，構成12×5階模糊評價矩陣：

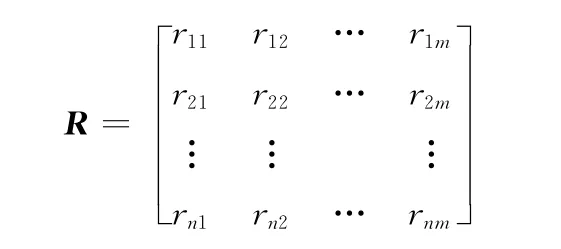
其中n＝12，m ＝5，rij＝μj（ui）。

需要說明的是，在模糊評估中，若按最大隸屬度判定原則，σ值對最終的評估結果影響不大［11］。按純數學的方法，σ一般取0．1或0．15。

2．4 權重系數的確定

考慮到各指標因素對整體系統的影響程度不同，評價過程中需對每一個指標引入權重系數加以衡量。目前，權重系數的確定方法有很多，主要分為主觀賦權法和客觀賦權法。常用的主觀賦權法有專家打分法、二項系數法、層次分析法等；客觀賦權法有變異值法、熵值法［12］。針對在機測量系統評價具有跨學科的特性，比較客觀合理的做法是采用專家打分法。

確定12項指標權重系數A0＝ （a1，a2，…，a12），其中ai代表指標因素xi的權重系數且。對于三個子系統來說，權重向量分別為 A1＝ （a1，a2，a3，a4），A2＝ （a5，a6，a7，a8，a9），A3＝ （a10，a11，a12）。

3 應用實例

MCH63機床（圖4）是國內較早采用箱中箱結構、同步雙驅、力矩電機等先進技術的四軸聯動精密臥式加工中心，加工中心配置FANUC 31i高性能數控系統和哈爾濱先鋒機電有限公司的TP6C紅外測頭（圖5）及其測量軟件，可實現在機測量。本文以該在機測量系統為對象，在試驗數據的基礎上運用上述正態模糊化方法對其整體性能進行模糊綜合評價。

圖4 MCH63精密臥式加工中心

圖5 TP6C紅外測頭及測量軟件

3．1 原始檢測數據

根據2．2節介紹的方法獲得子系統性能數據，部分數據如表2～表4所示，表3中“0．004 mm／300 mm”指的是在任意300 mm 的測量長度上允差為0．004 mm，其他類似。

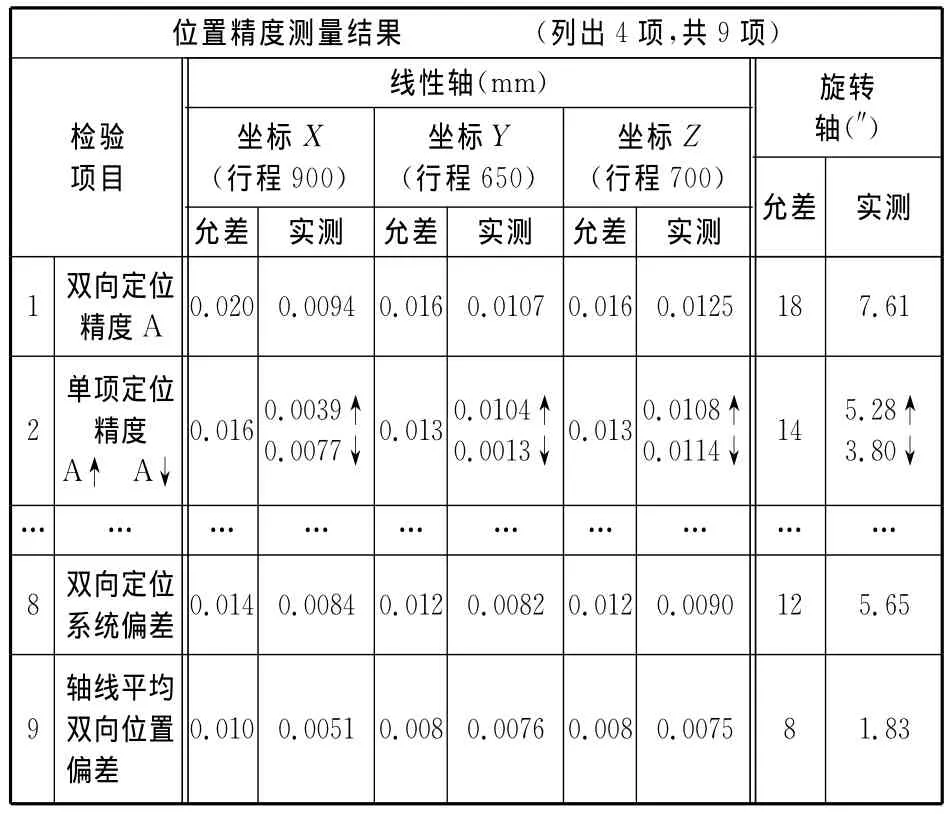
表2 機床位置精度測量結果部分數據

表3 機床幾何精度測量結果部分數據

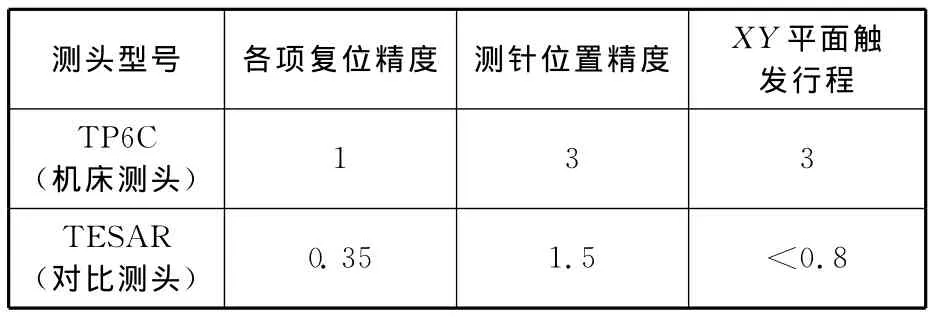
表4 測頭精度參數（常溫下測針長度取60 mm） μm

3．2 模糊評價矩陣確定

分析檢測數據，按照表1中計算公式對各性能指標值進行概率化處理，結果如表5所示。

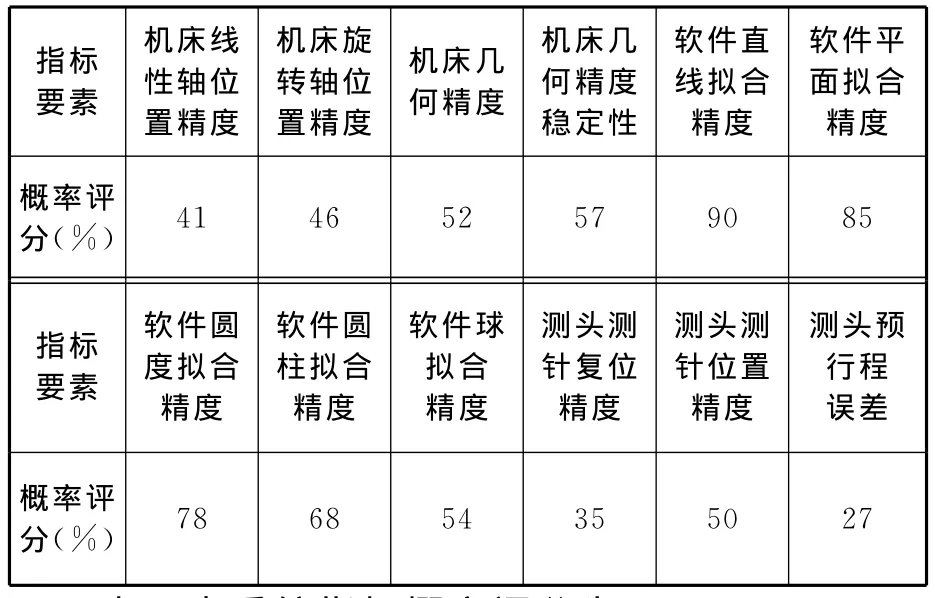
表5 各指標要素概率化評分

表5中系統指標概率評分為

取σ＝0．15，根據2．2節介紹的正態模糊化方法對各指標要素概率評分值進行模糊化處理，得到各指標評價矩陣的隸屬度值rij，如表6所示。

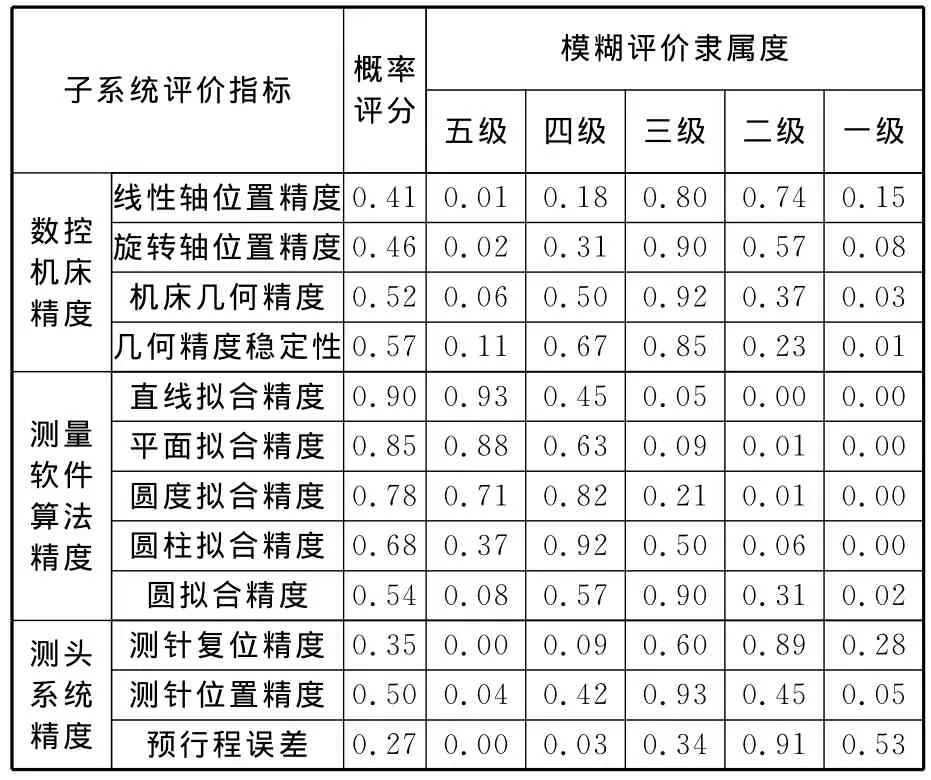
表6 模糊評判矩陣表

對表6中評價隸屬度數據作歸一化處理，得各子系統指標模糊評價矩陣如下：

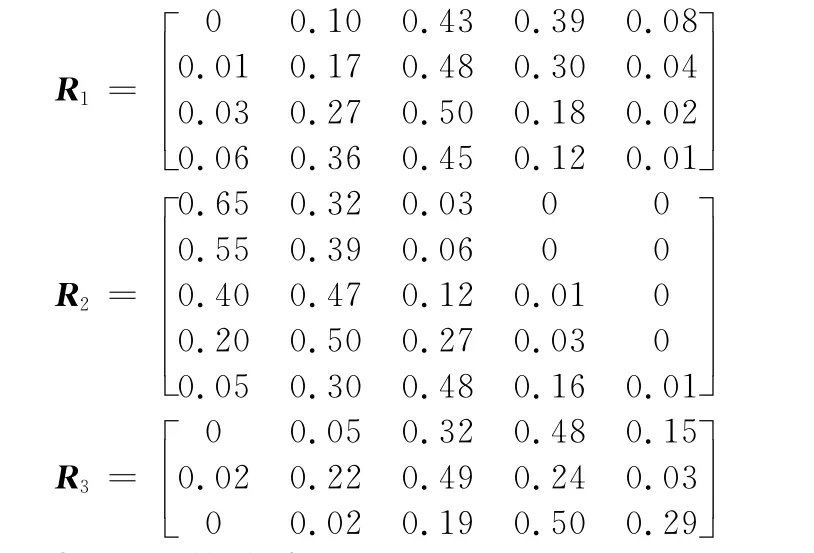
3．3 權重系數確定

與機床設計及質量檢驗人員討論，確定各指標權重系數，如表7所示。

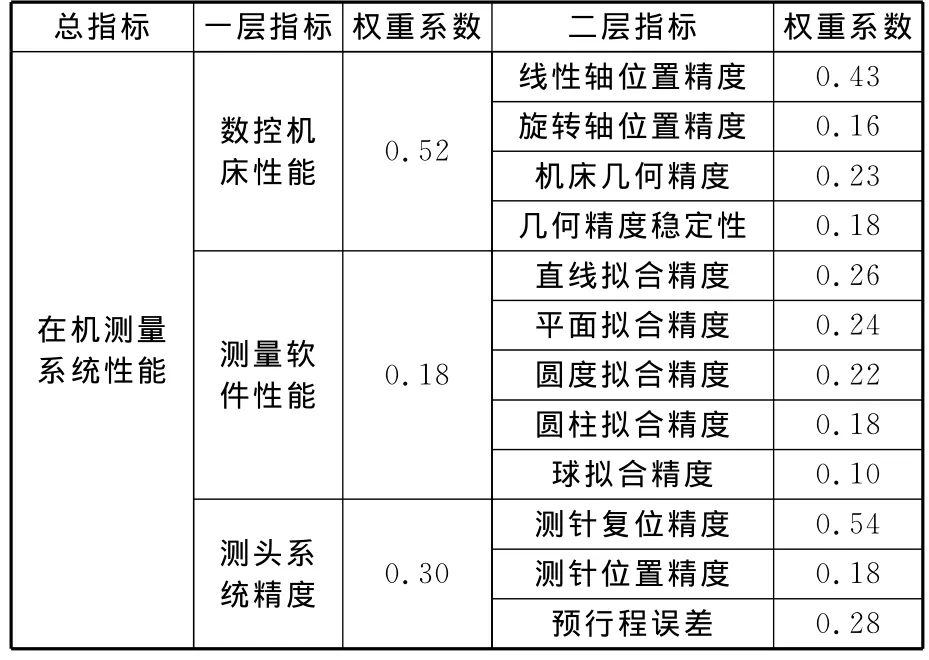
表7 評價指標權重調查統計結果

由此可得各層指標權重向量：一層指標權重系數A＝ （0．52，0．18，0．30），二層子系統指標權重系數 A1＝ （0．43，0．16，0．23，0．18），A2＝ （0．26，0．24，0．22，0．18，0．10），A3＝ （0．54，0．18，0．28）。

3．4 模糊評判結果及分析

在獲得了系統各層指標的權重系數和模糊評價矩陣后，根據式（1）進行模糊評判結果的計算。

首先，計算子系統的評價結果并根據最大隸屬度原則確定模糊評價結果：

B1＝ A1R1＝ （0．0193，0．1971，0．4577，0．2787，0．0472），可知數控機床子系統的精度評價為三級，其隸屬度為45．77%。說明機床精度較好，有較大的精度儲備量。

B2＝ A2R2＝ （0．43，0．4002，0．1452，0．0236，0．001），可知該測量軟件算法精度為五級，其隸屬度為43%。說明測量軟件算法的精度與標準軟件差距很小，軟件符合擬合計算要求。

B3＝A3R3＝ （0．0036，0．0722，0．3142，0．4424，0．1676），可知測頭系統精度為二級，其隸屬度分別為44．24%。說明測頭精度精度滿足要求，但與坐標測量機專用測頭相比還有一定差距。

再根據總系統指標的權重向量A＝（0．52，0．18，0．30），計算該在機測量系統模糊評判結果如下：

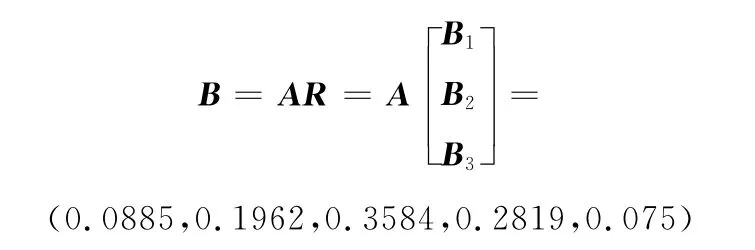
計算結果表明，該在機測量系統的整體精度儲備量等級為三級，其隸屬度為35．84%，說明系統整體性能較好。各評價隸屬度向量中未出現相同最大分量，因此評價結果是有效的。

評價結果表明，MCH63機床上的在機測量系統具有一定的精度儲備，說明該系統能滿足加工零件在機測量的要求。從評價過程和結果可知，測頭系統是該在機測量系統的相對薄弱環節，而數控機床精度對測量結果的影響最大。這一方面可通過補償測頭測針位置誤差和預行程誤差來解決，另一方面也應進一步提高機床的線性軸位置精度和幾何精度穩定性。

4 結束語

本文將多層模糊綜合評判理論應用到在機測量系統的性能評價中，綜合考慮了各子系統性能指標因素，在測試數據的基礎上采用正態模糊化方法建立模糊評價矩陣，通過模糊計算獲得了合理的評價結果。基于試驗數據模糊化處理的模糊評價方法實現了對具有定量指標的在機測量系統的正確評價。實例驗證了該方法的有效性，評價結果表明，該在機測量系統整體性能較好，可以用于零件的在機檢測。本文提出的評價方法也可解決在機測量系統組建過程中探測系統選購、機床選擇等模糊決策問題。

［1］ Cho M W，Seo T I．Inspection Planning Strategy for the On－machine Measurement Process Based on CAD／CAM／CAI Integration［J］．Advanced Manufacturing Technology，2002，19：607－617．

［2］ Kim S H，Ko T J，Ahn J H．Elimination of Settling Error Due to Clamping Forces in On－machine Measurement［J］．Advanced Manufacturing Technology，2002，19：573－578．

［3］ Kim K D，Chung S C．On－machine Inspection System Accuracy Improvement Using an Artifact［J］．Journal of Manufacturing Systems，2003，22（4）：299－308．

［4］ 劉麗冰，劉又午．加工中心在線檢測誤差補償技術研究［J］．中國機械工程，2000，11（3）：154－157．

［5］ 劉波．自由曲面的數控機床在線檢測及誤差補償技術研究［D］．天津：天津大學，2000．

［6］ 高峰，李艷，黃玉美，等．數控成形砂輪磨齒機的在機測量方法研究［J］．儀器儀表學報，2008，29（3）：540－544．

［7］ 朱劍英．智能系統非經典數學方法［M］．武漢：華中科技大學出版社，1999．

［8］ 海克斯康測量技術有限公司．實用坐標測量技術［M］．北京：化學工業出版社，2007．

［9］ 中國機械工業聯合會．GB／T17421－1998機床檢驗通則［S］．北京：中國標準出版社，1998．

［10］ 王為農．坐標測量機性能評價的國際標準［J］．中國計量，2004（2）：16－17．

［11］ 周穗華．概率型數據模糊化方法研究［J］．模糊系統與數學，2004，18（4）：59－63．

［12］ 劉曉婷，倪鳳英，王佑君．基于模糊評價的施工機械決策模型及應用［J］．機械科學與技術，2004，23（7）：834－836．