車輛擔保期內產品質量問題早期預警研究

涂華剛 林 燕 吳有成 金 平

上海大眾汽車有限公司，上海，201805

0 引言

企業擔保期內的索賠數據在可靠性工程中有許多重要的應用［1－6］，其中一個重要的應用和挑戰是，利用該數據與生產數據、銷售數據結合，對產品在市場上可能發生的質量問題進行早期檢測［7－8］。

本文在分析整車企業質量擔保期內的索賠數據的特性基礎上，提出了一種綜合千車故障數控制圖的市場質量問題早期監控策略，并就其核心算法原理、算法步驟、參數優化設計、系統實現以及實例分析等多個方面展開了較為詳細的論述。研究結果對于整車企業研究并監視其產品售后市場質量狀況具有借鑒意義。

1 索賠數據的統計特性分析

索賠數據的生命周期包含四個重要的時間特征，分別是生產日期tprod、銷售日期tsold、修理日期trepair及結算日期或索賠數據接收并確認日期treport。一個索賠數據的生成需經歷以下三個時間階段：從車輛生產完畢到車輛銷售成功的時間階段T1（即銷售時間），T1＝tsold－tprod；從車輛開始使用到進維修站修理的時間階段T2（即售后使用時間）；T2＝trepair－tsold；從索賠申請提出到認可或結算的時間階段T3（即數據接收及確認的時延），T3＝treport－trepair，T3為結算日期和索賠申請填報的修理日期的間隔天數。

銷售數據滯后T1的分布是影響故障率統計的一個重要分布。如果等待時間T1較短，會因抽樣量過小，涵蓋不全而導致一部分抽樣誤差出現，致使估計的變異性增大。只有足夠大的銷售月份偏移（offset）才能減小因抽樣誤差而帶來的影響。

現以某公司2004年的真實統計數據為例來分析索賠數據滯后T3的分布。該公司索賠申請的流轉時間為30天之內的約占總數的22%，60天內的約占80%，90天以內的約占95%，120天以內的約占99%。也就是說，一個索賠申請從提出到認可的整個過程所需時間T3約有3～4個月。即使在這段時間內生產過程發生了系統性變化，也很可能無從得知。這種數據滯后狀況的客觀存在，嚴重影響著故障率統計數據的及時性和完整性，這對于提早發現市場新問題和質量波動情況是極為不利的［4－6］。

抽樣等待時間間隔T的選擇取決于所需監控的使用月份數、數據填充的飽和度以及估計誤差的大小。其中T2即為所需監控的使用月份數（month in service，MIS），數據填充飽和度受T3影響，T1影響估計誤差的大小。

從以上分析可知，在一個生產周期內生產的車輛由于銷售時間T1的不同往往會具備不同的售后表現，且給定使用時間T2的索賠往往也分布在幾個不同的月份，因此需要三個維度對索賠數據進行多元分析［7］。

2 千車故障數及其歷史平均水平的定義和計算

整車或零部件的千車故障數是一個很重要的指標，常用于描述轎車的質量，其計算公式如下：

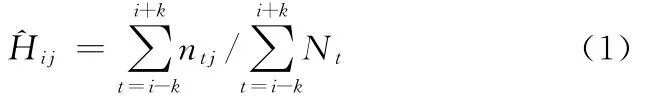
式中，ntj為生產月份t在給定使用月份j下所發生的實際故障數；Nt為給定車型在第t個生產月份下的抽樣量；k為指定的第i個生產月份下的前后月份偏移，k＝0，1或2。

在新車上市階段，如t≤0，可令ntj＝0，Nt＝0。

千車故障數的歷史平均水平的計算公式如下：

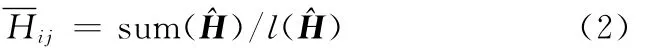
式中，Hij為第i個生產月份在第j個使用月份下對應的千車故障數歷史平均水平；＾H為指定歷史跨期（（i－m，i－1）下各生產月份千車故障數估計值的截尾向量；l（＾H）為向量＾H的長度。

為恰當反映出最近歷史的千車故障數真實狀況，同時避免因個別月份批量性千車故障數高點而對歷史平均水平的影響，本文采用各歷史時刻千車故障數估計值的移動截尾算術平均值作為千車故障數的歷史平均水平。通過采用歷史跨期中千車故障數介于25及75分位內的數據，可以將這段時期內千車故障數的歷史平均變化受批量問題的影響減小到最小。根據式（2），可得兩端截尾月份數lm為

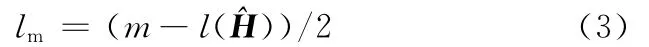
其中，m為定義的歷史時間跨度，m越大，千車故障數歷史平均水平表現出來的波動越平穩；但缺點是，對千車故障數的波動不能及時把握，會出現上升斜坡過長，報警的點數過多等現象。通常取m＝12，即對過去一年千車故障數平均水平予以評價。當m＝12時，可計算出截尾月份數lm＝3。計算lm的目的是為了排除因批量問題的發生對歷史平均水平的影響，以提升偵測時的靈敏度。

在新車上市階段，歷史時間跨度m可以通過以下公式獲得：m＝ED－ST，其中，ED為歷史終點，即ED＝i－（k＋1）；ST為歷史起點，即ST＝ED－12（最近一年）＋1；如果ST ＜1，那么令ST＝1。

歷史時間跨度m及兩端截尾月份數lm的選擇可參考表1所示的規則表。

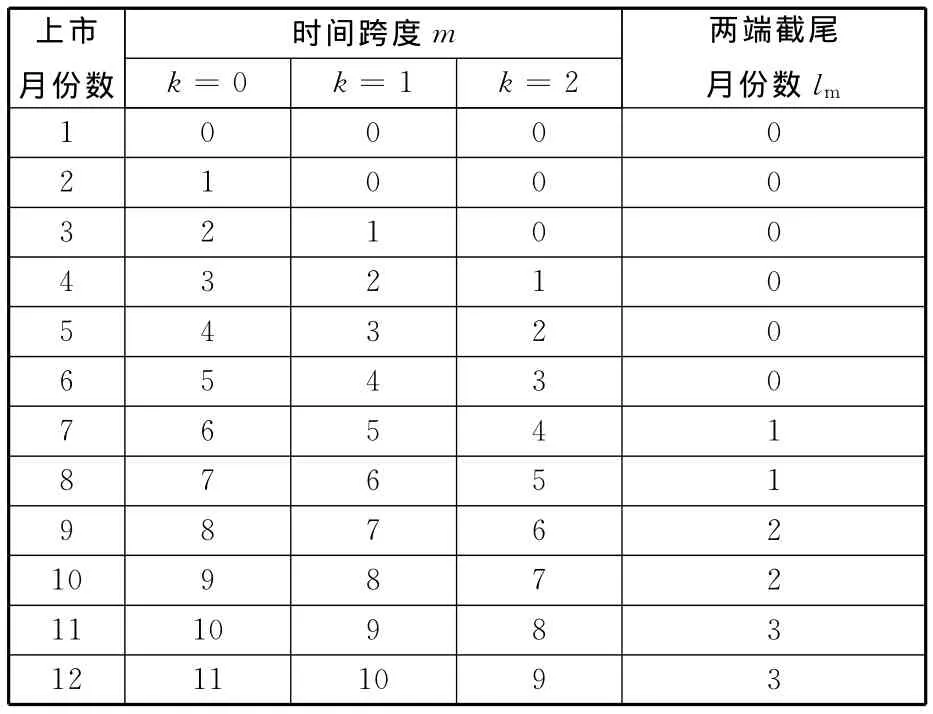
表1 歷史時間跨度及兩端截尾月份數選取規則表

3 千車故障數綜合控制圖

對于一個給定的生產周期，在一定的抽樣等待時間間隔T下，不同售后使用時間的故障率變化情況，可以通過比較實際故障率和預期故障率的大小來進行監控。其假設檢驗可表示如下［7］：

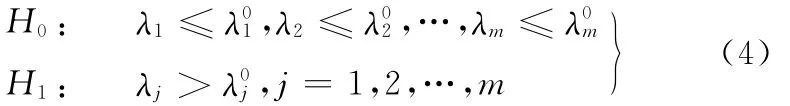
其中，對于售后使用時間j而言，λj代表實際的故障率而λ0j代表預期的故障率。

一般來說，我們認為：如果Sij＞Cij，對于第i為第i個生產周期生產的在第k個銷售周期出售的、處于第j個售后使用時間段的車輛的索賠數量；Cij＝，Cij為索賠總數量的臨界值，Uikj為第i個生產周期生產的在第k個銷售周期出售的、處于第j個售后使用時間段的車輛的預期索賠數量臨界值。Uikj與千車故障數的歷史平均水平Hij、生產后各個銷售周期內車輛的銷售數量Nik及誤報警概率α有關。

然而，在實踐中我們發現，當不合格數比率p即產品故障率以千車故障數為衡量基準時，基于上述原理設計的控制圖會遭遇零一決策（zeroone decision）、較高誤報警概率以及無法監視過程的瞬間變化等缺點［8］。

為了克服上述缺點，本文根據綜合控制圖（synthetic control chart）［9－17］原理構建了綜合千車故障數控制圖（Syn G）。Syn G控制圖利用了合格連串長度（CRL）以監視基于千車故障數的不合格數比率p的變化。CRL定義為兩個不合格品間的合格品長度（包含最終的不合格品）。使用CRL監視p變化的基本思想是：當p值變大，CRL值將期望變小；當p值變小，CRL值將期望變大。

由于CRL服從參數p之幾何分布，其期望值E（CRL）與累積分布函數F（CRL；p）分別為

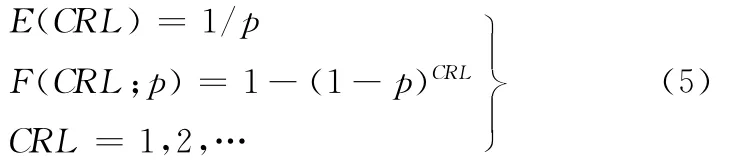
在誤報警概率α下，CRL控制圖之雙邊控制上下界限分別用UCL、LCL表示，可得

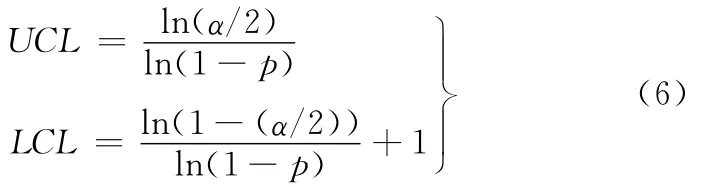
CRL控制圖之平均連串長度ARL定義為CRL控制圖顯示控制外信號平均所需的樣本點數，可由下式計算獲得［8］：

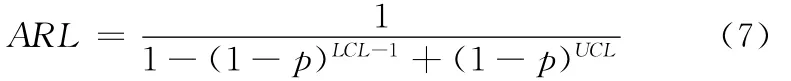
在實際運用中，如果僅需監控質量變差的情況，則只需單邊檢驗，由式（5）計算獲得［10］：

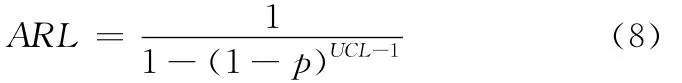
為進一步提升屬性控制圖的監視效率，考慮到生產過程的連續性問題，本文提出了算術加權移動平均Syn G控制圖來克服生產過程中相關性問題所帶來的影響。Syn G控制圖的基本設計思想是，將CRL控制圖中合格及不合格品視為Shewhart控制圖中樣本點未超出及超出其上控制邊界（監視千車故障數的增加，Shewhart控制圖僅需上控制邊界）的樣本，CRL控制圖中監視的不合格數比率即為Shewhart控制圖中樣本點超出其上控制邊界的概率。其算法步驟如下：

（1）在平均運行長度ARL指標約束下，對單邊檢驗（one－sided test）下的控制邊界（upper control bounds，UCB）及合格串長度CRL進行綜合優化設計，以決定Shewhart控制圖之上邊界UCB＊，CRL控制圖之下邊界L＊。

（2）計算監視月份在樣本大小為N下的千車故障數G 值，G ＝＾Hij。

（3）當G落于Shewhart控制圖之接受區域，此樣本視為CRL控制圖之合格樣本，轉步驟（2）；反之，此樣本視為CRL控制圖之不合格樣本，轉步驟（4）。

（4）計算目前樣本與上次視為不合格樣本之樣本長度（此次不合格樣本列入計算但不包含上次不合格樣本），此長度視為CRL控制圖之CRL觀測值。

（5）若L＊≤CRL，過程視為仍處于控制內狀態，轉步驟（2）；反之，過程被認為可能已改變至控制外狀態，轉步驟（6）。

（6）綜合控制圖顯示為控制外信號，即發出預警。

（7）對各車型所有零件重復上述步驟，找出所有可能風險零件列表。

（8）對所有風險零件按模糊層次分析法進行排序，確立各車型質量整改項目。

（9）展開質量分析，找出并消除導致質量問題系統性變差的可歸屬原因。當過程回復至控制內狀態后，轉步驟（2）。

4 參數優化設計

Syn G控制圖的設計通常基于ARL的表現，即當過程處于控制內狀態時，ARL必需較長，以保證較低的誤報率；當過程處于控制外狀態時，ARL必需較短，如此才能迅速發現過程的變化。

參數優化設計過程如下：

（1）給定控制內平均顯示時間（ARL1）以及CRL控制圖之邊界參數L（L為正整數），從L＝2開始，計算千車故障數G落于Shewhart控制圖之拒絕區域之外的概率α，由式（5）和式（8）可知：

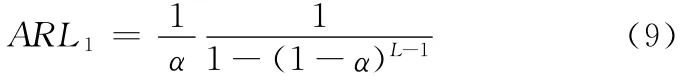
（2）當過程變壞導致千車故障數增加時，假設欲監測的控制外千車故障數為G＋ΔG，其中ΔG為千車故障數增量，ΔG＞0。當抽樣量為N時，根據步驟（1）求得的α，通過求解以下方程組，可得控制外漏報警概率β：

其中，UB 為Shewhart控制圖之控制邊界，Fαν11ν12、Fβν21ν22分別為臨界值為α，自由度為ν11、ν12及臨界值為β，自由度為ν21、ν22的F累積分布函數，它們是β的函數。控制內誤報警概率α表示生產正常情況下，純粹是由于偶然因素導致仍有一部分點子落入Shewhart控制圖之控制邊界拒絕域之外的概率。控制外漏報警概率β表示當生產發生異常波動時，仍有一部分點子可能會落入Shewhart控制圖之控制邊界可接受域之內的概率。千車故障數增量ΔG＞0，表示系統狀態變差。

將求出的β值代入下式，即可求出控制外平均運行長度ARL2：

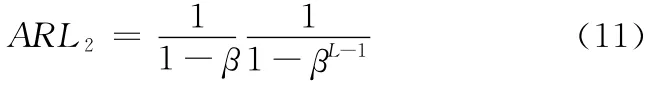
（3）如果目前之G＋ΔG控制外ARL2大于前一個，轉步驟（4）；否則，L←L＋1，轉步驟（2）。

（4）將前一個（L＊，α＊）組合，作為綜合控制圖的最佳設計參數。

（5）根據最佳設計參數組合（L＊，α＊）、待評價生產月份在最近一年內的千車故障數的歷史平均水平Hij，及待評價生產月份樣本大小N，由下式可得Syn G控制圖的控制邊界

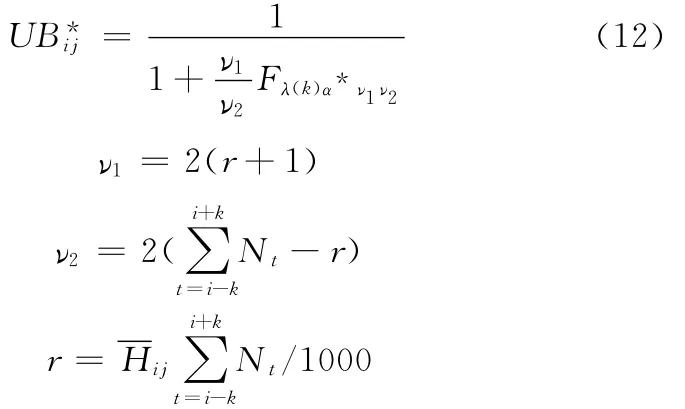
式中，λ（k）為記憶修正因子。

在實際設計時，針對實際千車故障數可能出現的較大過程偏移，可以采用監控長度ARL2≤3作為參數優化設計界限，來篩選固定優化參數（L＊，α＊）以簡化Syn G控制圖的設計。仿真結果顯示，雖然Syn G控制圖是為針對某特定欲監視過程偏移而設計的，但所有過程偏移之控制外ARL2均較Shewhart控制圖低。

此外，為了進一步提升大的過程偏移的監視效率，諸如階躍變化的過程偏移監視效率，通常還需指定一個千車故障數上邊界USB，USB可通過盡可能降低誤判概率α獲得。令ARL1＝12000，L→∞，這時可得誤報警概率α＝0．000 083，將其代入式（12）可得指定的故障數控制上邊界USB，超過該指定控制上邊界USB的監視月份將予以直接預警。

另外，為了提升問題預警的魯棒性（robust），我們還精選了遍布全國的27家中心維修站（27SST），并以江蘇、浙江、上海等核心銷售區域為抽樣重點進行數據監控。這些地區的索賠信息可能并不一定通過索賠結算系統的校驗，但是通過利用27SST的快速反饋信號，并采用一種所謂變抽樣區域（VSS）的方法，可以一定程度上確保知道目前顯示的樣本過程是否的確發生了系統性變化。

5 層次分析

本文采用層次分析法來篩選出真正意義上有風險的零件，并按優先級順序排序，以便質量保障部門能夠將紛繁復雜的質量信息集中加以管理，并實施集中統一協調。風險指數η的定義如下：

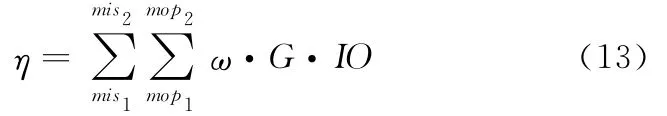
式中，ω為風險權重，時間越近權重越大；IO用來表示在對應的生產月份（month of production，MOP）和使用月份MIS是否有異常，為二元邏輯變量（TRUE，FALSE）；mop1、mop2分別為關注的生產月份范圍起止點，通常為一年或三個月；mis1、mis2分別為關注的使用月份數范圍起止點。

在企業具體實踐過程中，預警風險指數僅僅是層次分析所考慮的因素之一。索賠費用、是否為新增故障模式、措施落實情況、車型產銷量、問題的復雜性因素、用戶抱怨強度、安全性因素、概率損失，以及供應商水平等因素，都應該加以考察。

6 應用效果及預警實例

本文提出的設計思想和方法，已經在上海市重點產品質量攻關項目——上海大眾汽車有限公司市場質量信息預警系統（MOP／MIS預警系統）中得到了應用和實施，取得了良好的應用效果。以某車型某零件為例，其使用3個月（3MIS）的預警曲線如圖1所示，其數據狀態更新日期為2007－11－06，橫坐標為生產月份（“0411”表示2004年11月份，其余類似）。圖1中虛線表示基于上述預警算法所構建的預警系統認為可能有問題的生產月份。從圖1中可以看出，在2006－07～2006－11月中，過程控制環節出了一點小問題（殼體合模線未修導致泄漏）而影響了千車故障數曲線，接著正如我們所預料的那樣，從2007－05起千車故障數曲線一直呈明顯變壞的趨勢。此外，該零件按上述層次分析中的風險排名規則已列在第2位。通常，這樣的零件展示給主管工程師的信號應該是非常嚴重的。后經分析證實，該零件的模具在2007－05月時已出現嚴重老化問題。作為對比，按照傳統的MOP／MIS系統（不帶預警功能）中傳統的抽樣等待間隔來計算，在2007－11數據更新當月，其使用3個月的千車故障數至多只能展示到2007－04月份，即2007－04以后的點將無法展示，更不用說評價其好壞。另外，如果此時僅按其綜合平均千車故障數排名來計算的話，其整車排名則排在第196位，展示給質量分析工程師的印象是，該零件的質量狀況還是比較令人滿意的，根本看不出什么意外。該預警系統使專業部門發現市場出現可靠性問題的時間比以前足足早了4個月。

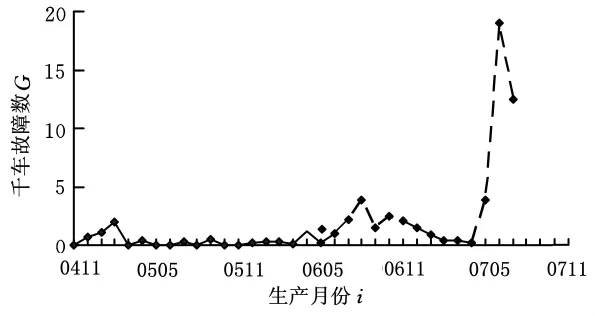
圖1 某車型某零件的預警實例

實踐表明，該預警系統已成為上海大眾汽車有限公司監視售后市場質量變化的重要工具。該預警系統的應用不僅全面提升了企業質量管理和監控的能力，而且可為企業每年節約1800萬元以上的索賠費用，其有效性已經在企業的生產實踐中得到了充分的驗證。

［1］ Karim M R，Suzuki K．Analysis of Warranty Claim Data：a Literature Review［J］．International Journal of Quality ＆ Reliability Management，2005，22（7）：667－686．

［2］ 張建國，許海寶．汽車質量保證期故障信息的可靠性分析方法［J］．中國機械工程，2000，11（5）：544－548．

［3］ Attardi L M，Guida G．Pulcini．A Mixed－weibull Regression Model for the Analysis of Automotive Warranty Data［J］．Reliability Engineering ＆ System Safety，2005，87（2）：265－273．

［4］ Alam M M，Suzuk K．Reliability Analysis of Automobile Warranty Data Using Censoring Information Related to Random Failures［C］／／Proceedings of the 5th Asian Quality Congress．Incheon，Korea，2007：542－547．

［5］ Rai B，Singh N．Hazard Rate Estimation from Incomplete and Unclean Warranty Data［J］．Reliability Engineering ＆ System Safety，2003，81（1）：79－92．

［6］ Rai B，Singh N．Forecasting Warranty Performance in the Presence of the‘Maturing Data’Phenomenon［J］．International Journal of Systems Science，2005，

36（7）：381－394．

［7］ Wu H，Meeker W Q．Early Detection of Reliability Problems Using Information from Warranty Databases［J］．Technometrics，2002，44（2）：120－133．

［8］ Xie M，Lu X S，Goh T N，et al．A Quality Monitoring and Decision－making Scheme for Automated Production Processes［J］．International Journal of Quality and Reliability Management，1999，16（2）：148－157．

［9］ Honari B，Donovan J．Early Detection of Reliability Changes for a Non－Poisson Life Model Using Field Failure Data［C］／／RAMS 2007Proceedings．Orlando，2007：346－349．

［10］ Huang H，Chen F．A Synthetic Control Chart for Monitoring Process Dispersion with Sample Standard Deviation［J］．Computers and Industrial Engineering，2005，49（2）：221－240．

［11］ Chen F L，Huang H J．A Synthetic Control Chart

for Monitoring Process Dispersion with Sample Range［J］．The International Journal of Advanced Manufacturing Technology，2005，26（7）：842－851．［12］ Davis R B．Woodall．Evaluating and Improving the Synthetic Control Chart［J］．Journal of Quality Technology，2002，34（2）：200－208．

［13］ Wu Z，Spedding．A Synthetic Control Chart for De

tecting Small Shifts in the Process Mean［J］．Journal of Quality Technology，2000，32（1）：32－38．［14］ Wu Z，Yeo S H．Implementing Synthetic Control Charts for Attributes［J］．Journal of Quality Technology，2001，33（1）：112－114．

［15］ Scariano S M，Calzada M E．A Note on the Lower－sided Synthetic Chart for Expnoentials［J］．Quality Enginerring，2003，15（4）：677－680．

［16］ Calzada M E，Scariano S M．The Robustness of the Synthetic Control Chart to Non－nomality［J］．Communications in Statistics－Simulation and Computation，2001，30（2）：311－326．

［17］ Costa A F B，Rahim M A．A Synthetic Control Chart for Monitoring the Process Mean and Variance［J］．Journal of Quality in Maintenance Engineering，2006，12（1）：81－88．