基于廣義信息熵測度的制造過程質量評估

張根保 曾海峰 王國強 張家為

重慶大學，重慶，400030

0 引言

制造過程是產品質量形成過程中的重要環節，在確認產品設計質量的前提下，它是實現產品設計質量的關鍵。從信息論的角度看，制造過程的復雜性是指描述制造過程狀態所預期需要的信息量。復雜性的程度稱為復雜度，制造過程的復雜度越大，表明不確定性和不可預測性越大，進行過程建模所需的信息就越多［1］。目前，國內外對制造復雜性的研究主要集中于生產運營層面，如生產調度、企業物流及資源分配等［2－6］，文獻［7－9］從人因工程的角度分析了制造過程的復雜性，文獻［10］研究了復雜產品的裝配決策問題，提出通過防差錯設計的裝配規劃等來降低復雜性，但這些研究未能對造成復雜性的根本原因進行解釋和分析，而且很少系統分析制造過程的復雜性對質量控制的影響。

為保證產品制造質量，必須了解復雜性對制造過程的影響、控制過程向隨機性演化的趨勢。過程運行復雜性行為與開放系統的熵變特性是一致的，根據耗散理論，制造系統的有序結構是在非平衡條件下通過物流、信息流和控制流的作用得以維持的［11］。信息熵與過程有序度之間存在一定的關系，即過程的信息熵大，其有序程度低；反之，過程的有序程度高，則其熵小。這樣，通過分析信息熵的變化，然后利用復雜度與過程有序度的關系，就可以用動態復雜度來描述系統的質量狀態和演化方向。應對制造過程中的復雜性策略可以分為兩種：一種是盡量避免、降低和消除制造過程的復雜性；另一種是理解和管理復雜性，通過對制造過程的定量描述和定性分析，預測和控制過程的質量［12－13］。然而無論采用哪種策略，都必須理解和衡量過程的復雜性。

為定量描述制造系統中的復雜性現象，本文對信息熵理論進行擴展，建立基于規模、難度和狀態多樣性的廣義信息熵模型，然后按照復雜性對時間的依賴關系，將制造過程的復雜性分解為靜態復雜性和動態復雜性，利用廣義信息熵模型來研究制造過程復雜性的測度方法，并將其用于過程質量控制評估，從復雜性的角度給出過程質量控制有效性的定量測度方法。

1 復雜性的測度

1.1 信息熵的基本概念

在物理學中，熵是表征系統運動混亂程度或系統狀態數量豐富程度的物理量；而在信息論中，熵又能描述系統的不確定性和復雜程度。制造系統作為復雜開放系統，每個確定的系統狀態都對應著一種有序的要素結構，系統狀態的轉移意味著一種新的有序結構的出現［14］。按照信息論對熵的定義，設離散型隨機變量X具有n種可能的取值 （x1，x2，…，xn），且各值的概率分別為 （p1，p2，…，pn），則 X 的熵定義為［13，15］

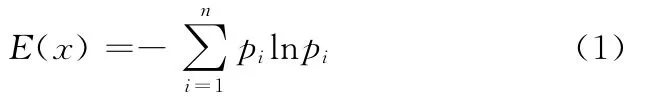
1.2 復雜性測度的廣義信息熵模型

僅依照信息熵描述復雜度，難以完整表達制造過程中的規模復雜性現象（如特征、工序的數目等），而忽略規模復雜性顯然與實際情況不符，標準信息熵模型的另一個缺陷是無法充分利用設計、制造、工藝人員的經驗信息。為此根據制造系統的特點，參照文獻［7］的復雜度模型，從數量、多樣性和相對難度三個方面考慮，建立復雜性測度的廣義信息熵模型（extended information entropy model，EIEM），如圖1所示。其中數量或規模造成的復雜性要素為

式中，N為對象規模或數量。

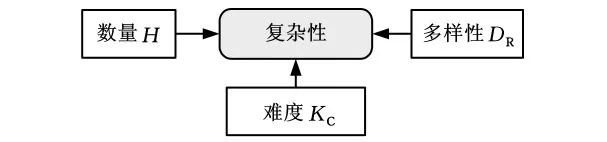
圖1 復雜性測度的廣義信息熵模型

狀態多樣性造成的復雜性要素采用下式計算：

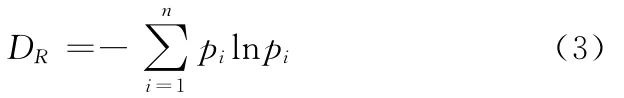
式（3）中pi由對象的狀態劃分確定。本研究將過程／工步劃分為正常或特定異常，對于有n種狀態的工步PS，異常狀態種類為n－1，即將對象 劃 分 為 PSSn，PSS1，PSS2，…，PSSi，…，PSSn－1，其中PSSn表示正常狀態，PSS1，PSS2，…，PSSn－1為特定異常狀態。PSSi概率的具體值pi由工步在該狀態下持續的時間TPSSi確定，為便于計算，要求按照異常狀態的主因對工步狀態進行明確的劃分，即在特定時間工步的狀態屬性必須是唯一的，于是pi＝TPSSi／T，其中T為工步PS的總持續時間。

實現難度造成的復雜性用難度系數KC表示，如工序的復雜性隨其實現難度的增加而增加。KC具有主觀性和和模糊性的特點，因此需采用模糊評價、灰色評價等描述不確定性屬性的方法計算。

本文采用三角模糊數進行評判，計算過程中綜合運用模糊集理論和層次分析法，以三角模糊數代替常規層次分析法中的標度，確定KC的實現難度。KC的評價步驟如下：①確定評價人員或評價小組，確定待評的過程／工序，建立實現難度評價的層次模型；②確定三角模糊評語等級；③建立模糊判斷矩陣；④計算各過程／工序在隸屬于同一準則的各考核指標下的實現難度評價分值；⑤計算在各準則及總目標下的評價結果向量，根據計算結果獲得各過程／工序實現難度的評價向量，具體計算過程參見文獻［16-17］。

根據以上方法獲得的實現難度為相對實現難度，對特定過程／工序／工步的質量評估，可以直接運用相對實現難度計算，此時隱含假設難度最小的過程為標準過程，并以模糊評價相對難度系數作為實現難度。如果要利用本方法對多個制造過程進行質量比較，需計算絕對實現難度，此時只需確定某過程的實現難度為標準過程難度，通過與相對難度系數對比，就可求出以標準過程難度為基準的各過程的絕對實現難度。

結合以上三個要素，復雜性測度的廣義信息熵模型為

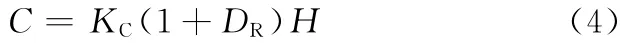
式（4）不但能夠捕捉對象狀態變化造成的動態復雜性，而且表達了對象規模造成的復雜性，比單獨采用信息熵模型或組合規模復雜性模型更符合制造過程復雜性的實際情況。同時，式（4）通過H和DR從客觀角度衡量對象的復雜性，通過KC從主觀的角度搜集設計、制造、工藝人員的經驗信息，其測度要素比單純依賴主觀評估的復雜性度量模型更全面。

2 制造過程的復雜性測度

2.1 制造過程的復雜度

制造過程的復雜度與產品的需求密切相關［1］，產品制造需滿足設計要求，因此工件的材料、加工工序、設備類別、夾具、檢驗量具、運行模式等影響制造過程的因素都可能造成復雜性。按照復雜性的來源和特點，我們將這些要素歸為工藝復雜性、過程復雜性及由兩者造成的系統宏觀運行復雜性三類，三類復雜性之間的關系如圖2所示。

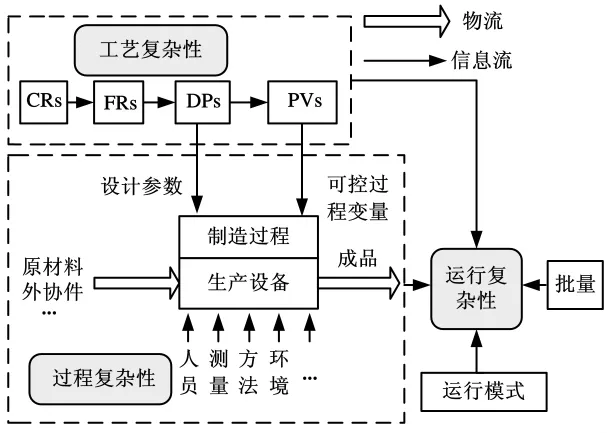
圖2 制造系統復雜性分解

工藝復雜性在設計過程中產生，同樣功能的產品，如果工藝方案不同，制造過程的復雜性也不同，因此需考慮從顧客需求 （CRs）→功能需求（FRs）→設計參數（DPs）→過程變量（PVs）各轉化過程；過程復雜性描述將DPs轉化為實際物理特征中的不確定性，因此過程復雜性應涵蓋了制造資源約束下的工序能力及制造過程中5M1E產生的隨機影響；運行復雜性主要關注系統宏觀上是否按預定的調度計劃運行，如果系統按預計的調度計劃生產運行，制造系統的運行復雜性保持不變，系統處于受控狀態，當系統的內外環境的變化導致調度計劃與實際狀態偏離時（如臨時產品的加工、設備故障、調整運行模式等），系統運行復雜性增加［13］。

制造過程的復雜性就是產生于這些要素的多樣性和不確定性，為便于利用復雜性測度的廣義信息熵模型描述制造過程的復雜行為，按照對時間的依賴性把過程復雜性分為靜態復雜性及動態復雜性。定義加工過程為P＝ ｛P1，P2，…，Pi，…，Pcn｝，Pi＝ ｛PSi1，PSi2，…，PSij，…，PSici｝，PSij＝｛PSSij1，PSSij2，…，PSSijk，…，PSSijcij｝，其中Pi為加工過程的第i道工序，PSij為工序Pi的第j道工步，PSSijk為工步PSij的第k個狀態，cn為工件加工所需的工序數目，ci為工序Pi所含工步數目，cij為工步PSij的狀態數目。

2.2 制造過程靜態復雜度

過程的靜態復雜度是描述制造過程預期狀態所需要的信息量，用CS表示。CS主要由工藝方案及實現工藝方案所涉及的制造資源決定，不隨時間變化。文獻［1］把來源于多可選加工設備和多加工路線造成的復雜性稱為虛擬復雜性（imaginary complexity），其實質是資源的組合優化問題，一般采用遺傳算法、蟻群算法、免疫算法來解決［18］。虛擬復雜度在產品的加工方案、工藝流程確定之后降為0，此時加工設備及路線都是確定的，因此過程靜態復雜度不需要考慮虛擬復雜性。根據復雜性測度的廣義信息熵模型，制造過程靜態復雜性的數量要素Hi直接通過工步數目計算：

根據式（3），制造過程中工步PSij的靜態多樣性要素：

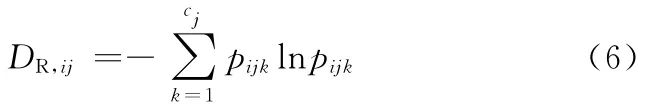
式中，pijk為工步PSij第k個狀態的概率。

根據式（2）～ 式（4），工序Pi的靜態復雜度表達式為

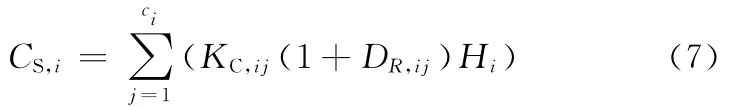
綜合式（5）～式（7），工件制造過程的靜態復雜度為

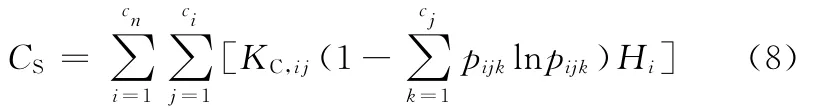
過程的觀測尺度對CS的值影響較大，而觀測尺度取決于對系統的關注點及可操作性等方面的考慮。為了便于比較和分析，對離散制造系統，取工步作為最小觀測尺度，工步內或更小尺度上的狀態變化不計入復雜性度量范疇。當然，根據分析需要也可以設置更大或更小的觀察尺度，如分析水輪機、船用主軸這類大型工件的加工過程時就需進一步細分，以便考察和分析工步內的復雜性規律。

KC，ij采用模糊評價確定，評價指標主要有材料的可加工性、設備的加工能力、產品特征的工藝性、質量要求、質量檢驗難度等。評價決策人員由來自設計、工藝和制造部門組成，以綜合利用這些人員的經驗信息。

理想條件下制造過程各工步的預期狀態為設計期望，因此靜態過程為確定狀態系統，DR，ij＝0。工藝設計方案在本質上決定了數量要素Hi和難度系數KC，ij，從而確定了系統的靜態復雜度。

2.3 制造過程的動態復雜度

靜態復雜度只考慮產品制造的期望狀態，而動態復雜性則需要進一步關注制造過程中實際發生的狀態，即制造過程中的狀態不確定性。制造過程在運行中的實際狀態由過程檢測或狀態監測獲得，當加工狀態偏離期望時，系統的熵增加，對任意工序Pi，其動態復雜度由下式計算：

綜合式（9）、式（10），工件制造過程的動態復雜度為

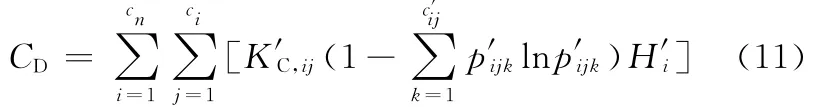
其中，D′R，ij為工步PSij的動態多樣性要素，K′C，ij為PSij的動態難度系數，H′i為Pi的動態數量復雜性要素，D′R，ij為動態多樣性要素，c′n為實際加工中所用的工序數目，c′i為實際加工中工序Pi所含工步數目，c′ij為實際加工中工步PSij的狀態數目，p′ijk為工步PSij處于第k個狀態的概率，在加工期間如果工藝設計方案不變，則K′C，ij＝ KC，ij，H′i＝ Hi，否則需重新評估。

如果加工過程保持在期望狀態，則D′R，ij＝DR，ij。實際上，由于受到人員、設備、材料、外界環境等因素的隨機影響，加工狀態是圍繞期望狀態波動的，因此D′R，ij＞DR，ij。設工步PSij的狀態數目為c′ij，其期望狀態概率為p′ij1，則其他狀態數目為c′ij－1，且有

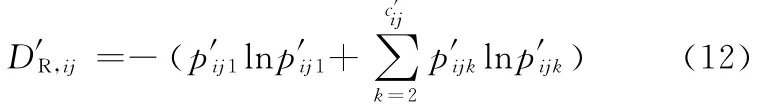
狀態發生變化并不意味著發生故障，如為了保證加工精度而定期對夾具、刀具進行必要的調整，這種加工狀態的變化就不屬于故障狀態。但是由于這種調整打斷了正常的加工，同樣增加了復雜度，因此狀態復雜度又可表示為

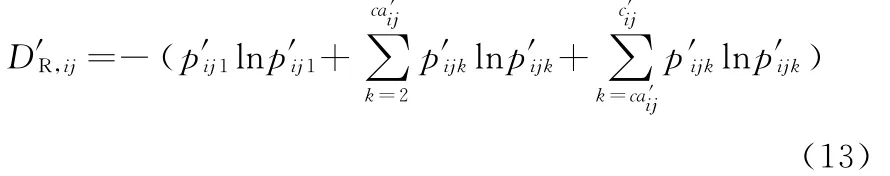
其中，ca′ij為工步PSij調整后正常狀態的數目，工步PSij故障狀態的數目為cij－ca′ij－1。為便于比較，與靜態復雜性一致，D′R，ij同樣取工步為最小觀測尺度，狀態發生的概率根據實際統計數據確定。當以工步為最小觀測尺度時，如果調整未打斷正常加工工序，則調整不計入狀態復雜性，如機床的自動補償。

3 基于復雜度的過程質量評估

3.1 過程質量的有效性評估

過程質量的有效性是指過程控制達到預期結果的程度。根據AD信息公理，信息量最小的過程，制造的產品滿足設計要求的概率最大，因此可以利用靜態復雜性和達到質量控制要求時的動態工序復雜性對過程質量的有效性進行描述。加工過程由于受到各種隨機因素的擾動，不可避免地會發生偏離，但工序的K′C，ij和H′i不變，所以動態復雜性的變化主要來源于D′R，ij，根據式（13），D′R，ij的變化又可以分為兩種類型：

類型1 在出現異常前主動中斷工序進行調整，調整后工件質量符合要求，此時D′R，ij的第二增大。這種情況增加了加工過程的復雜度，但是加工狀態的變化屬于質量控制下的調整，因此有利于質量控制有效性的維持和改進。

類型2 在發生狀態異常，工件加工質量不符合要求時中斷工序，則此時D′R，ij的第三項增大，這類復雜性除了造成生產中斷外，還導致返工和廢品等，破壞了工序的有效性。

D′R，ij發生類型1的變化說明企業已經掌握了工序變化的信息和規律，并且能夠利用這些信息進行工序調整。但必須注意的是，過度頻繁地中斷生產進行工序調整將增大加工成本，而且這種調整對工序質量控制的改進是有極限的，因此需設定合理地調整周期以保證成本和質量的最佳平衡。當D′R，ij變化源于類型二變化時，如果狀態異常造成的質量異常超過規定比例，則說明工序能力過低，必須進行工序改進。

根據以上分析，質量控制的動態有效性可用下式評估：

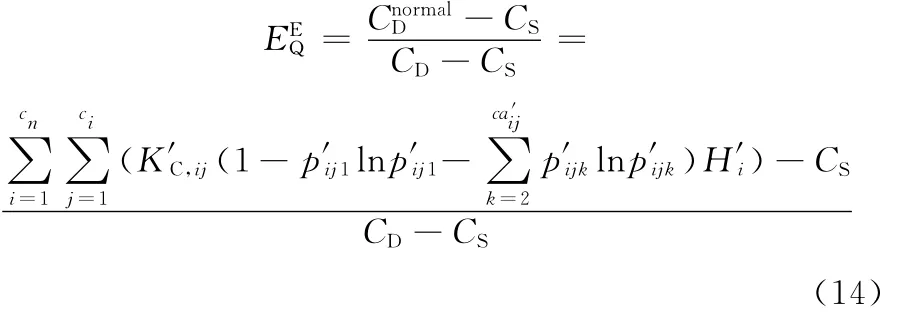
其中CnormalD為工件加工質量正常情況下的復雜度，計算方法參見式（9）～ 式（13）。

過程的動靜態復雜度的一致性反映了加工過程在內外部環境擾動條件下，保持穩定的加工質量的能力，可作為過程健壯性評估指標，通過下式計算：

如果加工過程的兩個類型的狀態多樣性水平都很低，表明過程的抗擾動能力相對較強，在無需過多過程維護的情況下也能保證加工質量和較低的故障水平。

利用基于復雜度的定量分析對現行質量控制方案進行評估，則可以幫助企業分析控制方案的有效性，深入分析造成復雜性的原因，找出質量改進的方向和途徑。

3.2 基于復雜度的質量監測

為保證產品制造質量，需監測制造過程的動態變化，控制過程向隨機性演化的趨勢。通過監測C′D的平均變動，然后利用復雜度與過程有序度的關系，就可以用動態復雜度來描述過程的質量狀態和演化方向。設從t0開始，以Δt為統計周期對加工過程進行監測（Δt大于最小觀測尺度），則t1時的過程復雜度為，可根據式（9）計算，因此動態復雜度在t0－t1期間的相對平均變動為

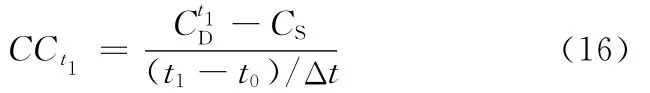
通過對復雜度變化的持續監測，得CCt＝｛CCt1，CCt2，CCti，…｝，根據這些數據就可判斷過程有序度的變化，從而估計質量的狀態和變化趨勢。

4 案例研究

某企業的齒輪加工過程包括毛坯粗加工、半精加工及精加工等7道工序，23道工步。齒輪具體參數如下：模數m＝2．25mm，齒數z＝50，壓力角α＝20°，螺旋角β＝20°，毛坯為45鋼，毛坯外形尺寸為φ121mm×68mm，其他參數如圖3所示。工序10到工序40采用CA6140車床加工，三爪自定心卡盤定位。滾齒工序50采用Y3150加工，芯軸定位。工序60采用X6132銑床加工。

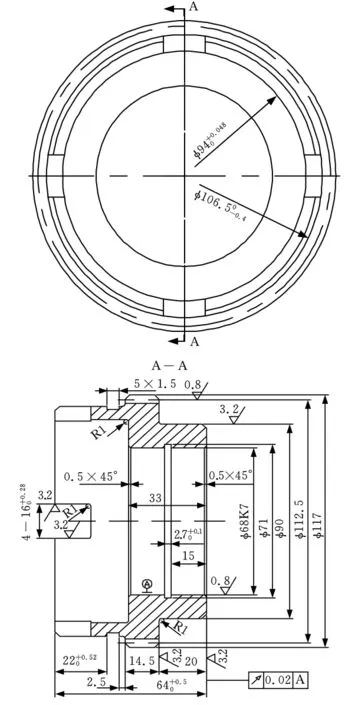
圖3 車床齒輪零件圖

4.1 齒輪加工過程的靜態復雜度

首先確定齒輪加工的數量復雜性和難度復雜性要素。數量復雜性要素根據齒輪加工的工步數目確定，表1列出了齒輪加工的主要工序、工步及其內容以及一些參數。難度系數通過模糊決策方法確定，評價決策人員來自于設計、工藝和制造部門。在靜態復雜度計算之前，先用Grubbs檢驗法對可疑數據進行檢測，剔除異常值和粗大誤差數據，保證數據的一致性和可用性。表1直接給出評估結果（KC列），根據式（8），齒輪加工過程的靜態復雜度為14．03。

4.2 齒輪加工過程的動態復雜度

為簡化計算，本算例假設加工期間工藝設計方案不變，因此動靜態數量復雜性和難度復雜性要素相同（表1中 H 和KC列），即K′C，ij＝KC，ij，H′i＝ Hi。本例觀察周期Δt取40h（5×8h），表1中第5列和第6列分別為在出現異常前主動中斷工序進行調整的概率和加工質量異常中斷工序的概率。由于篇幅關系未列出具體各狀態類別和具體數據，只給出這兩類類型發生的總概率。下面以滾齒工序為例，給出兩類狀態多樣性的計算方法。

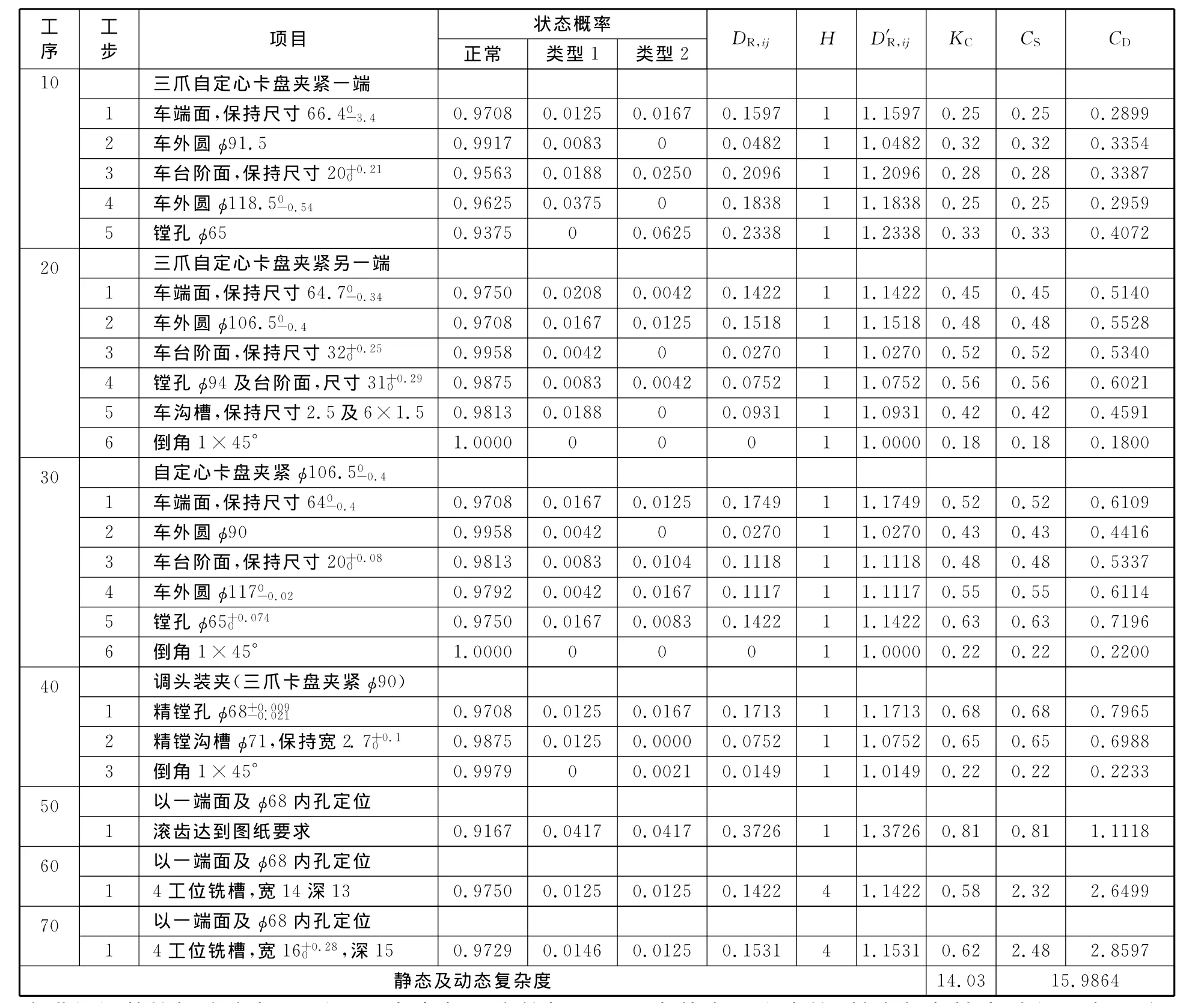
表1 齒輪加工工藝及復雜度算例

滾齒工序在觀察周期內，工作正常的概率p′ij1＝2200／（40×60）＝0．917；定時進行滾齒機刀具檢查耗時100min，p′ij2＝100／（40×60）＝0．042；因齒向誤差超差，調整壓緊螺母和墊片耗時40min，p′ij3＝0．017；因為滾刀崩刀導致加工的輪齒表面同一部位產生縱向的溝紋，通過軸向竄動滾刀解決，耗時60min，p′ij4＝0．025，根據式（13），可知D′R，50，1＝0．3726。其他各工序D′R，ij計算方法類似，計算結果見表1中第9列。根據式（11），計算得最終動態復雜度為15．9864。

4.3 齒輪加工過程質量控制的有效性評估

加工過程質量控制的有效性按照式（14）評估：

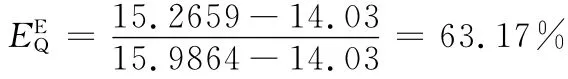
這說明過程中的動態復雜度中有63．17%是過程正常狀態下產生的，其余復雜性由過程異常導致，為無效復雜性。進一步對表1第6列狀態概率進行具體數據分析，發現鏜孔工步10－5和滾齒工步50－1為造成異常類復雜性的重要原因。

根據式（15），過程的靜動態復雜度的一致性指標為

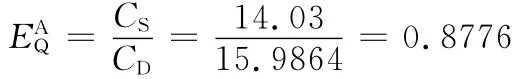
齒輪加工過程的靜動態復雜度的一致性不高，為0．8776，說明過程的健壯性不高，為保證加工質量，加工過程中不得不進行大量調整和維護活動。

結合上述指標EEQ和EAQ分析，由于齒輪加工過程健壯性差，導致過程的抗擾動能力相對比較弱，因此必須依賴過程調整和維護活動保證工件加工質量。這種做法雖然保證了產品的質量水平，但是質量成本較高。必須找出提高過程穩健性的措施才能從根本上提高過程質量。對表1數據進行分析，我們提出如下改進措施：改進齒輪的毛坯加工和熱處理工藝以提高毛坯精度，同時校準滾齒機，并強化齒輪加工規程。

根據式（16）計算平均動態復雜度，實施質量改進措施后持續監測平均動態復雜度8周，圖4為基于復雜度的質量監測圖，質量改進后平均復雜度從1．96下降到1．41，相比未改進前降低28%，同時加工合格率從79．6% 提高到97%。為從統計上檢測質量改進的顯著性，對質量改進前后合格率、平均復雜度進行假設檢驗。

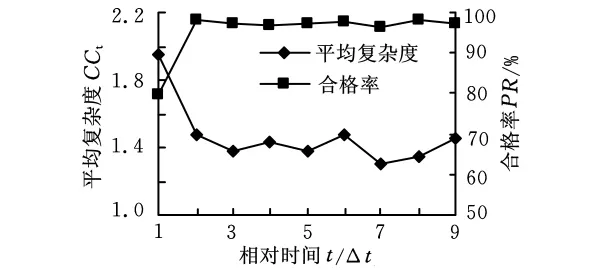
圖4 基于復雜度的齒輪加工過程質量監測圖

取改進前后各8周的數據，利用配對樣本（d1，d2，…，d8）來檢驗，di＝Xi－Yi，Xi、Yi分別為質量改進前后的合格率＼平均復雜度。配對樣本可以看作是來自正態總體N（d，σ20＋σ21）的樣本，此時σ0≠σ1，n0＝n1，對于平均復雜度，檢驗假設H0：d＝0，H1：d＞0，由于方差σ20＋σ21未知，絕域為T＞tα（n－1）。經計算得平均復雜度tco＝tα（n－1）＝t0．01（7）＝ 2 ．9998，tco＝ 1 4．25 ＞2．9998，故拒絕H0，即認為平均復雜度顯著降低。同理，計算得合格率tcf＝15．6＞2．9998，故認為改進后合格率得到顯著提高。可見與質量改進前相比，質量改進措施有效降低了齒輪加工過程的復雜度，提高了合格率。

本案例利用廣義信息熵模型對齒輪加工質量進行了評估。評估綜合了數量要素、實現難度和狀態多樣性要素造成的復雜性，比單純采用信息熵模型、規模復雜性模型或主觀評價模型更為全面。

從本案例可以看出，通過廣義信息熵模型的過程數量復雜性和難度復雜性要素，可以進行制造過程靜態評估。本例中齒輪加工過程的靜態復雜度評估值為14．03，而單獨采用信息熵模型，無法進行制造過程的靜態復雜性評估；廣義信息熵模型通過納入狀態多樣性要素，實現對齒輪加工過程質量評估的動態化。例如，在實施質量改進措施后，制造過程的平均復雜度從1．96下降到1．41，而規模復雜性模型在產品的設計方案和工藝方案確定以后就不再變化，是一種靜態評估模型，無法體現制造過程中質量狀態的改變；主觀評價模型由于一般不進行動態評價，因而也無法對兩次之間制造過程質量的變化作出響應，而廣義信息熵模型中將實現難度的評價值以加權系數的形式處理，在綜合設計、制造、工藝人員主觀經驗信息的同時，避免了無法進行動態制造過程質量評估的問題。

5 結束語

過程控制是產品制造質量控制的重要方法，制造過程中的復雜性導致過程建模、預測和控制困難。為保證產品制造質量，必須了解復雜性對制造過程的影響，控制過程向隨機性演化的趨勢。制造過程中的信息熵與其復雜度成反比關系。為定量測度制造過程中的復雜性，本文對信息熵理論進行擴展，建立了基于規模、難度和狀態多樣性的廣義信息熵模型；然后提出利用此復雜性測度模型，進行制造過程靜態和動態復雜度的測度方法，并將其用于制造過程質量控制評估，從復雜性的角度給出了過程質量控制有效性的定量評價方法；最后通過實例展示了該理論和方法的有效性。需注意的是，熵量計算是一種宏觀定性方法，通過廣義信息熵的測度實現制造過程復雜性的量化，是針對復雜制造過程的一種間接評估方法。對制造過程中可直接量化的過程質量特性，采取質量統計方法評價更為簡潔和準確。本文提出的復雜性測度理論和方法為描述和分析制造過程提供了一個新的視角和方法，可應用于制造系統可靠性、健壯性等其他方面的分析。

［1］ Nam S．Axiomatic Design：Advances and Applications（the Oxford Series on Advanced Manufacturing）［M］．London：Oxford University Press，2001．

［2］ 姚倡鋒，張定華，彭文利，等．面向復雜零件網絡化制造的資源優化配置方法［J］．計算機集成制造系統，2006，12（7）：1060－1067．

［3］ 吳正剛，韓玉啟，宋華明，等．復雜產品的模塊化制造戰略研究［J］．中國機械工程，2005，16（20）：1826－1830．

［4］ Cho S，Alamoudi R，Asfour S．Interaction－based Complexity Measure of Manufacturing Systems Using Information Entropy［J］．International Journal of Computer Integrated Manufacturing，2009，22（10）：909－922．

［5］ Papakostas N，Efthymiou K，Mourtzis D，et al．Modelling the Complexity of Manufacturing Systems Using Nonlinear Dynamics Approaches［J］．Cirp Annals－manufacturing Technology，2009，58（1）：437－440．

［6］ Siemieniuch C E，Sinclair M A．On Complexity，Process Ownership and Organisational Learning in Manufacturing Organisations，from an Ergonomics Perspective［J］．Applied Ergonomics，2002，33（5）：449－462．

［7］ Eimaraghy W H，Urbanic R J．Modelling of Manufacturing Systems Complexity［J］．CIRP Annalsmanufacturing Technology，2003，52（1）：363－366．

［8］ Eimaraghy W H，Urbanic R J．Assessment of Manufacturing Operational Complexity ［J］．CIRP Annals－manufacturing Technology，2004，53（1）：401－406．

［9］ Eimaraghy W H，Urbanic R J．Modelling of Manufacturing Process Complexity［J］．CIRP Annalsmanufacturing Technology，2003，52（1）：363－366．

［10］ Zhu X W，Hu S J．Karen Y，et al．Modeling of Manufacturing Complexity in Mixed－model Assembly Lines［J］．Journal of Manufacturing Science and Engineering－transactions of the Asme，2008，130（5）：1－10．

［11］ 尹曉虎，錢彥嶺，楊擁民，等．基于熵的裝備維修系統效能評估與仿真［J］．系統仿真學報，2008，20（16）：4404－4407．

［12］ Efstathiou J．The Utility of Complexity［J］．Manufacturing Engineer，2002，81（2）：73－76．

［13］ 饒運清，Efstathiou J．基于信息熵的制造系統復雜性測度及其在調度中的應用［J］．機械工程學報，2006，42（7）：8－13．

［14］ 汪澤焱，益曉新．基于基點和熵的系統評價指標賦權法［J］．解放軍理工大學學報，2002，3（3）：91－95．

［15］ 張志峰．離散制造企業生產物流的熵模型評價及其應用［D］．武漢：華中科技大學，2008．

［16］ 姬東朝，宋筆鋒，喻天翔．模糊層次分析法及其在設計方案選優中的應用［J］．系統工程與電子技，2006（11）：1692－1694．

［17］ 曹柬，周根貴．一種新的敏捷虛擬企業合作伙伴選擇與評價方法［J］．中國機械工程，2004，15（22）：2009－2013．

［18］ 劉金山，廖文和，郭宇．基于雙鏈遺傳算法的網絡化制造資源優化配置［J］．機械工程學報，2008，44（2）：189－195.