混沌信號在抗干擾測量應用中的數字化處理

黃進燕,李嘉席

(1.西安電子科技大學,陜西西安710071;2.中國電子科技集團第五十四研究所,河北石家莊050081)

0 引言

混沌是非線性動力學系統特有的一種形式,是非線性系統中出現的類隨機現象,其基本特征是對初始條件的敏感,加之在時域和頻域具有可觀的主旁瓣比以及較好的距離和速度分辨率,使得混沌信號具有極強的抗干擾性和極低的截獲概率。混沌在電子工程中的應用研究領域已體現在測量、通信以及電子對抗等多個方面,特別是在電磁環境日趨復雜的背景下,混沌信號突出的抗干擾性能尤顯重要。

混沌信號的產生主要有兩類:一是由非線性電路直接產生功率譜合乎要求的超寬帶混沌信號,比較典型的有以Colpitts電路為基礎的一類電路和高維RC電路。另外一種就是由迭代或者數字方式產生較低頻率的混沌信號,再由其調制產生特定頻譜的超寬帶信號。一般是以混沌調相或混沌調頻的形式出現,在混沌雷達研究比較領先的國家,已經在研究一些實用性的基于混沌的雷達系統。本文針對抗干擾測量的應用背景,分析以Logistic映射為例的混沌信號的數字化處理和實現方案。

1 混沌信號在抗干擾測量系統中的應用

抗干擾測量系統由多路數字混沌信號產生器產生數字混沌信號經調相后進行變頻、濾波功放等處理后由天線發射出去。接收部分將天線接收的回波信號經低噪混頻后形成視頻信號采樣為數字信號后與多路數字混沌信號產生器產生的多路數字混沌信號進行相關處理,獲取距離信息并進行多普勒估計從而得到速度信息。系統框圖如圖1所示。

通過控制多路數字混沌信號產生器產生不同延時間隔的數字信號,即可實現不同的距離分辨力。本文側重討論混沌信號的數字化處理。

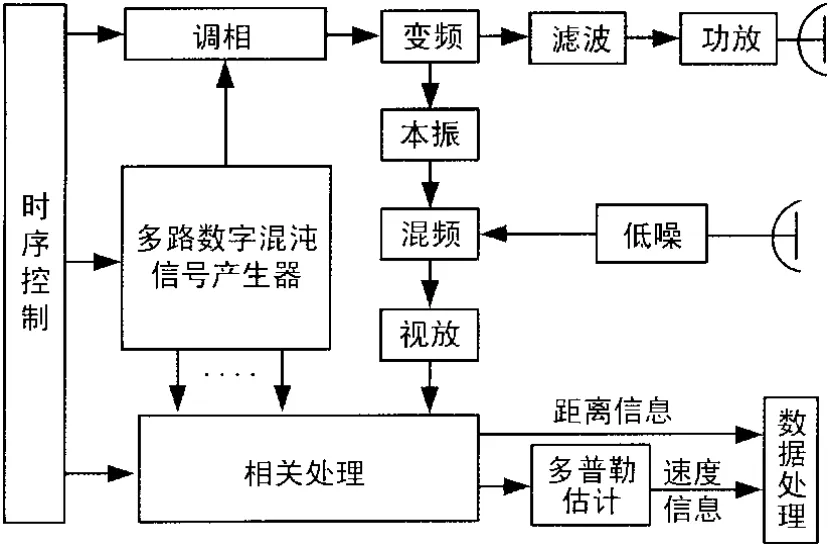
圖1 抗干擾測量系統框圖

2 Logistic映射

2.1 信號模型

Logistic映射具有多種形式,但各種形式間均可通過參數調整而相互轉換。其中最具代表性的Logistic映射表達式為:

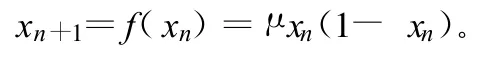
式中,μ∈(1,4];x∈(0,1)。

該式對應的是一個確定性可實現的非線性系統,可用于“預測”以xn為起點的下一個x值。研究結果表明,該動力學系統具有以下特點:

①系統輸出狀態取決于參數 μ,而同初始值x0無關。當μ∈(1,3]時,系統輸出很快收斂于(0,1)間的某一常值,此時稱作穩態,當 μ∈(3,4]時,穩定的不動點從吸引子變成排斥點,如圖1(b)所示,即在μ=3處,穩定的周期一單線開始一分為二,大約在μ=3.449 6時周期二又分叉為周期四。隨著 μ的增加,倍周期分叉越來越快,經n次分支,周期長度為2n,當 μ=μ∞≈3.571 448時,映射成混沌映射;

②在混沌映射時,系統具有初值敏感性、非周期等特性。所謂初值敏感性即在初始狀態,2個相互很接近的值會隨著時間的推移按指數分開;而非周期形是指此時輸出信號時域表現出雜亂無章,頻域表現出廣譜性,相關函數近似為沖擊函數,故又稱似白噪聲特性(或廣譜特性)。

2.2 信號特性分析

為了獲得最大的隨機性,取μ=4。從而獲得典型的Logistic映射:

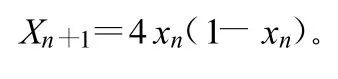
由此式仿真(取信號初始值x0=0.49)得到Logistic映射的信號波形、功率譜、自相關函數的仿真結果如圖2所示。

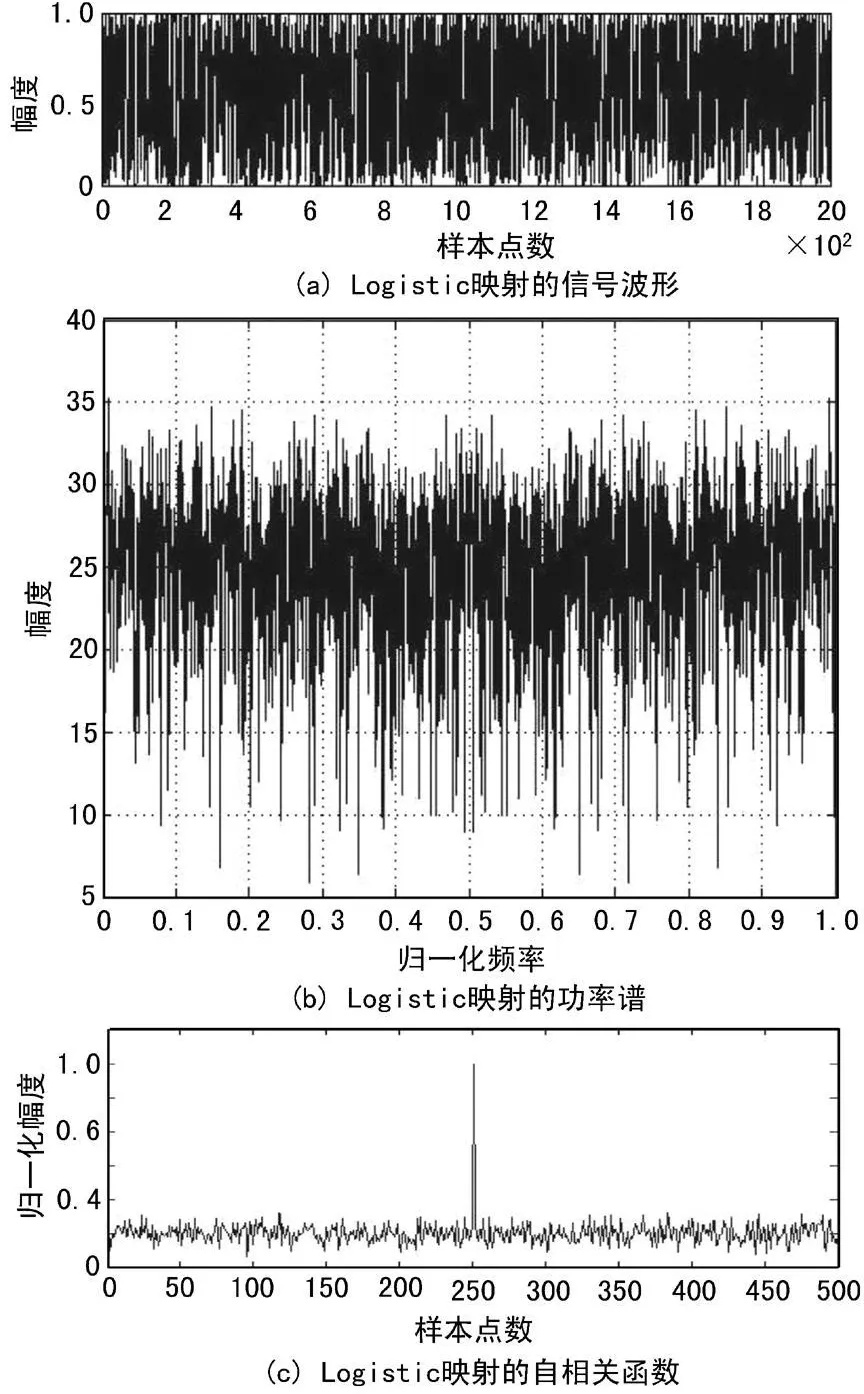
圖2 Logistic映射特性的MATLAB仿真結果

由仿真結果可知所選取的Logistic映射頻譜平坦,其自相關峰值尖銳具有良好的自相關特性,從而有很好的抗干擾特性。

2.3 信號模糊函數分析

模糊函數(Ambiguity Function,AF)是波形設計與分析的工具,它可以方便地刻畫波形與對應匹配濾波器的特征。AF在分析分辨率、副瓣性能以及多普勒和距離模糊方面非常有用,另外也可用于對距離-多普勒耦合的分析。

根據PM.woodward的定義[1],對于隨機特性的信號應采用平均模糊函數形式。但對于實際信號處理的時限性,采用樣本平均方式更現實一些。若信號處理時間為T,則混沌信號的平均模糊函數可以表示為:

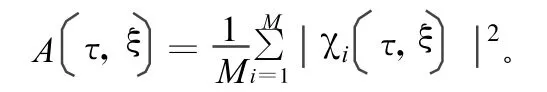
式中,i為第i個樣本函數;τ和ξ分別為時間和頻率,

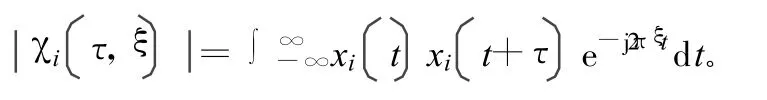
對離散時間信號有:

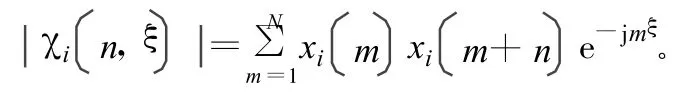
式中,m,n分別為時間變量和時間延遲。在計算中,可令所以上式可用DFT計算:

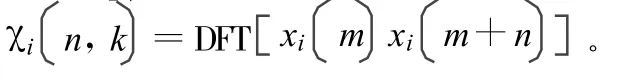
所以對應的模糊函數為:

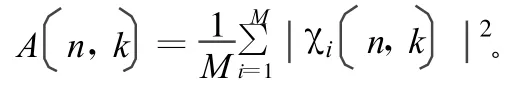
采用MATLAB進行仿真,取10個樣本,每個樣本100個點,仿真結果如圖3所示。

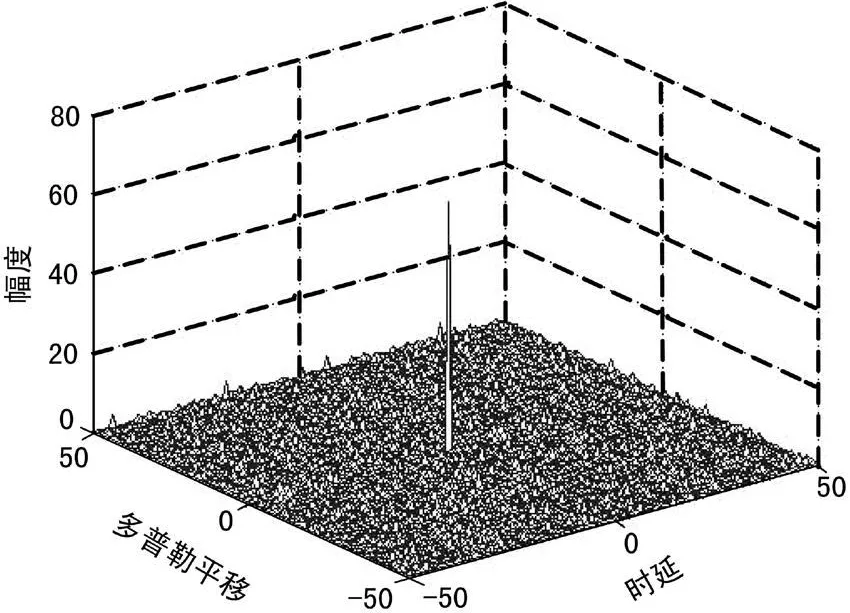
圖3 Logistic映射的模糊函數

由圖3可以看到該混沌序列具有狹窄的中心峰值,即具有很高的距離和多普勒分辨率。較均勻的平坦區域說明具有低的且均勻的旁瓣從而使遮擋效應最小化。對于測量系統來說,這都是非常有益的。

由于在實際工程中所獲得的不是理想的混沌信號,而是經過截斷后的混沌序列。所謂截斷的混沌信號實際上是對理想連續混沌信號的加窗處理。其模糊函數(時域加窗)[2]為:

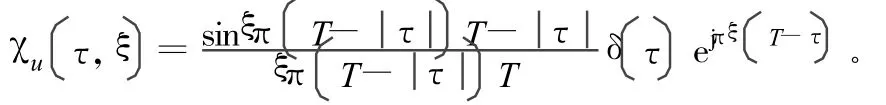
模糊圖變成刀刃形,不過模糊面積在理論上為零,因此仍具有極佳的測距測速精度。

3 混沌信號的數字化處理

3.1 Logistic信號數字化

對于一般的混沌映射xn+1=f(xn),概率密度ρ(x)可由Perron-Froenious方程得到,即

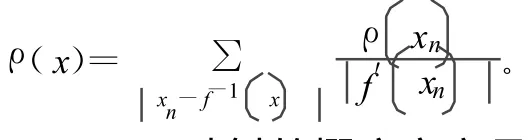
取μ=4,Logistic映射的概率密度函數為:

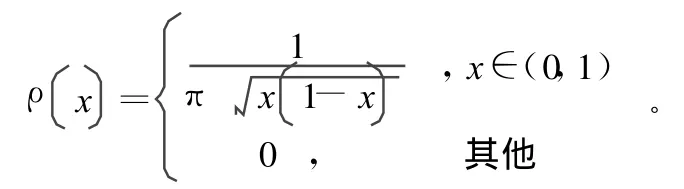
以初始值x0代入Logistic映射方程開始迭代,就可以得到混沌序列此時生成的混沌序列為實值序列,實際應用中需要對其進行數字化,得到二進制混沌序列。數字化方法有對稱量化、門限量化、分布量化和比特抽取量化等,其中對稱量化應用廣泛。對稱量化是將間隔I=[d,e]劃分為d=t0＜t1＜…＜t2m=e,劃分應滿足下列條件為一組對稱的門限,得到二進制函數為:

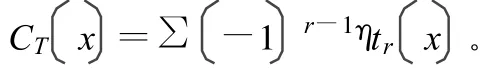
稱為門限對稱二進制函數。一般將該函數應用于不變側度具有對稱性的映射上,即滿足:

Logistic映射滿足此條件,其均值為1/2,故以1/2為界,將它們數字化為-1和1,即得到數字混沌序列為:

由平衡性知:數字化后序列均值為0,即ˉC=0。

3.2 有限精度效應

由于混沌序列的遍歷統計特性是建立在生成序列無限精度的基礎上,然而實際的迭代運算并不能滿足這個條件,只能在有限精度下進行迭代運算,這就產生了有限精度效應,即數字產生方法受有限字長的影響,就會使得所生成的混沌序列常常趨于周期性,或者是收斂于穩定解0。解決這一問題的有效方法可以在迭代的過程中分別對序列中的每個元素加入一個微小的擾動,從而破壞其周期性。目前降低混沌序列實現精度的方法主要有收縮法、m序列擾動法和正弦擾動法等。根據文獻[3]的分析,正弦擾動法是最為簡單且對精度要求不高。其表達式如下:

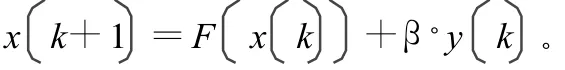
3.3 數字實現

采用ALTERA的FPGA實現Logistic信號的數字化。有限精度含義如下:如混沌映射的數值為01123456…,精度為1/100時,在處理時用100乘以0.123456…得到123.456…,取整后為123,在迭代計算的過程中,都用整數進行計算。同時,加入正弦擾動。其實現框圖如圖4所示。

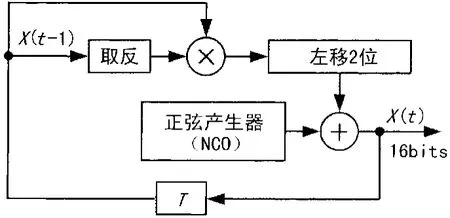
圖4 Logistic序列FPGA實現框圖

產生的序列數據經PCI總線由計算機獲取并存儲,對其頻譜、自相關函數進行分析,分析結果表明產生的序列的統計特性良好,符合Logistic的混沌映射特性。

4 結束語

研究了以Logistic混沌信號為例的混沌信號數字化處理及實現,通過分析混沌信號的頻譜、自相關特性和模糊函數,其強抗干擾性及較高的距離速度分辨力非常適用于抗干擾測量系統。

在FPGA中實現了Logistic混沌信號的在有限精度下的數字化處理,使得生成的序列具有較好的相關性能。采用該方法生成的混沌序列在抗干擾測量系統中有著較好的應用前景。

[1]WOODWARD PM.Probability and Information Theory with Application to Radar 2nd ed[M].New york:Pergam on Press,1964.

[2]謝紅梅.基于混沌理論的信號處理方法研究[D].陜西:西北工業大學博士論文,2003:89-94.

[3]吳芝路,任廣輝,趙 楠,等,混沌擴頻序列有限精度研究[J].哈爾濱商業大學學報,2006,22(1):42-45.