層次分析法中的指數型標度問題研究

王立民,楊振宇,白漢斌,李俊美

(1.北京系統工程研究所,北京100101;2.軍事科學院,北京100091)

0 引言

層次分析法是系統分析工具之一,它通過兩兩比較的方式確定層次中諸元素的相對重要性,然后綜合決策者判斷,確定諸元素相對重要性的總排序。整個過程體現了人的決策思維的基本特征,即分解、判斷、綜合,為許多定性分析研究提供了定量分析的簡便方法[1]。在層次分析法應用過程中,最重要步驟就是對同一層次各元素的重要性進行兩兩比較,從而構造判斷矩陣。如果能對兩兩比較的重要性程度進行定量測量,就可發揮定量分析的作用,這個定量測量的工具就是標度[2]。

1 層次分析法

用層次分析法作系統分析,首先要根據問題的性質和要達到的總目標,將其分解為不同組成元素,并按元素間的相互關聯影響及隸屬關系將元素按不同層次組合,形成一個多層次分析結構模型,并最終把系統分析歸結為底層相對于高層的相對重要性權值確定或相對優劣次序的排序問題。在排序計算中,每一層次的排序可簡化為一系列成對元素的判斷比較,并根據一定的比率標度將判斷定量化,形成比較判斷矩陣;通過計算判斷矩陣的最大特征值和它的特征向量,即計算出某層次元素對于上一層次中某一元素的相對重要性權值,這種排序計算稱為層次單排序,為了得到某一層次相對上一層次的組合權值,用上一層次各個元素分別作為下一層次各個元素間相互比較判斷的準則,得到下一層次元素相對于上一層次各個元素的相對重要性權值,然后用上一層次元素的組合權值加權,即得到下一層次元素相對于上一層次整個層次的組合權值,這種排序計算稱為層次的總排序。依次沿遞階層次結構由上而下逐層計算,即可計算出底層元素相對于高層的相對重要性權值或相對優劣的排序值。

從層次分析法步驟中可看出,為形成判斷矩陣,通常引入了1-9比率標度方法,這使得決策者判斷思維數學化[3]。這種將判斷思維數學化的方法大大簡化了問題的分析,使復雜定量問題分析成為可能,此外這種數學化方法還有助于決策者檢查并保持判斷思維的一致性,這充分體現了定性與定量相結合的思想,也即合理地對兩兩比較的重要性程度進行定量測量,如果定量測量可以做到,就可以發揮數學中定量分析的作用,決策過程也會比較容易。因此,層次分析法的基礎和核心問題是標度問題。

2 層次分析法的標度

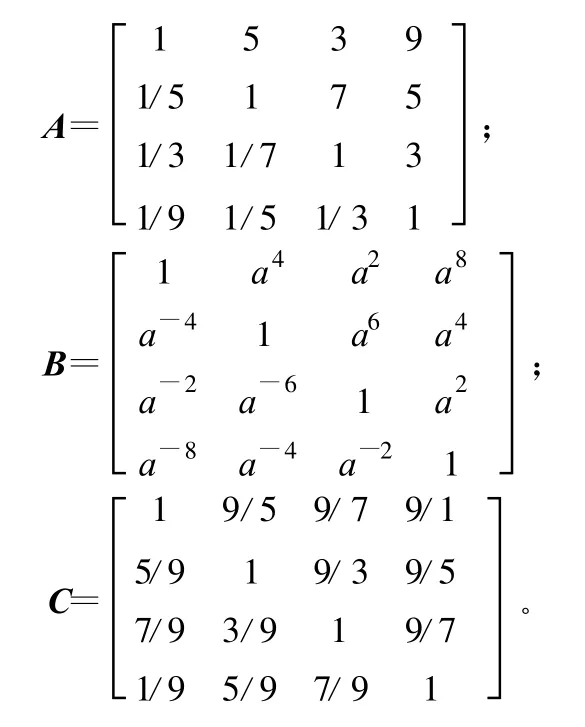
所謂標度是將定性分析轉化為定量判斷的一種數量指標,是根據人們對客觀事物觀察所得經驗決定的[4]。標度分為絕對標度和相對標度。在層次分析法中,為了形成判斷矩陣,通常引入了1-9比率標度方法,但在實際應用中,通常采用的1-9比率標度方法暴露出許多不足,如標度的比值與人們實際的判斷相差太遠;矩陣一致性與思維一致性脫節;實際結果與思維判斷不一致等等問題[5]。因此,很多學者從不同的觀點,提出了許多不同的標度系統,如互反型標度、互補型標度等。互反型標度是指采用一些離散的點標度來構造互反判斷矩陣,其中1-9標度、指數標度和分數標度如表1所示。互補型標度是通過元素間重要性程度之差得到的,幾種常用的互補型標度如表2所示。

表1 1-9標度、指數標度和分數標度

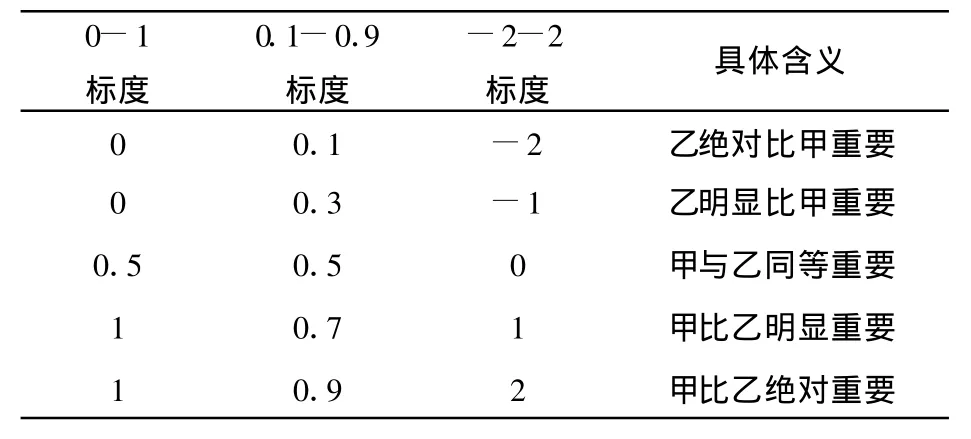
表2 幾種常用的互補型標度

眾多的標度之間存在差異,由不同的標度所構造的判斷矩陣,其一致性也不相同,得出的方案的排序權值也不相同,有的甚至會發生逆序。因此,如何選擇一種合理的標度系統是一個亟待解決的問題,下面將對使用最多的互反型標度作重點分析研究。

3 互反型標度選擇問題研究

在層次分析法中,當判斷矩陣的階數n=1,2時,正反互判斷矩陣是完全一致的;當n≧3時,對于同一個決策問題,由不同標度所構成的判斷矩陣,一致性就存在差異現象。下面用數學方法證明常用的互反型標度完全一致性互不相容。

設?aij∈A,?bij∈ B,aij=s,ajk=m,aik=t,由A的完全一致性可知:sm=t。

假若B完全一致:

當s,m≥1時,由表1標度之間的對應關系可知

由B的一致性:

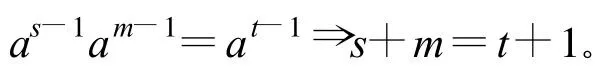
當s＞1,m≤1,t≥1時,由表1標度之間的對應關系可知。

由B的一致性:

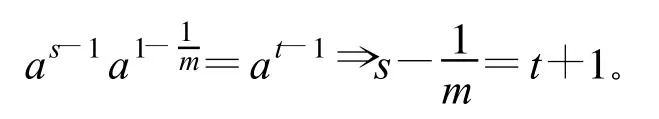
當s＞1,m≤1,t≤1時,由表1標度之間的對應關系可知

由B的一致性:

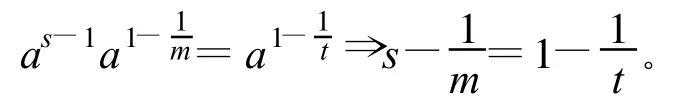
當s＜1,m＜1,t＜1,此時與上述3種情況中的某一結果相同。

從證明過程可以看出,在 3種情況下,總有aik=ajk或ajk=aik,由于i,j,k的任意性,A中的任意3行元素至少有2行對應相等,這與命題矛盾。同理可證明B,C,可見,表1中幾種常用的互反型標度的完全一致性互不相容。

從以上結果可以看出,標度系統的選擇對于決策結果至關重要,不同的標度系統有可能會產生完全不同的結果,對于如何選擇合適的標度系統,下面用實驗的方法進行進一步分析。

這里取A,B,C分別為1-9比率標度,an指數標度,9/9-9/1標度下的判斷矩陣,對于同一個問題的判斷矩陣,使用一致性比例檢驗法進行檢驗。

分別計算各個判斷矩陣的最大特征根λmax,然后計算一致性檢驗指標接著用Matlab程序計算樣本容量10 000的3～9階矩陣的RI值,其結果如表3所示,最后得到各個判斷矩陣相應的CR值(CR=CI/RI)。按同樣方法,構造不同標度下的不同階數的判斷矩陣,通過Matlab程序進行大量實驗,100次實驗結果的統計平均如表4所示。

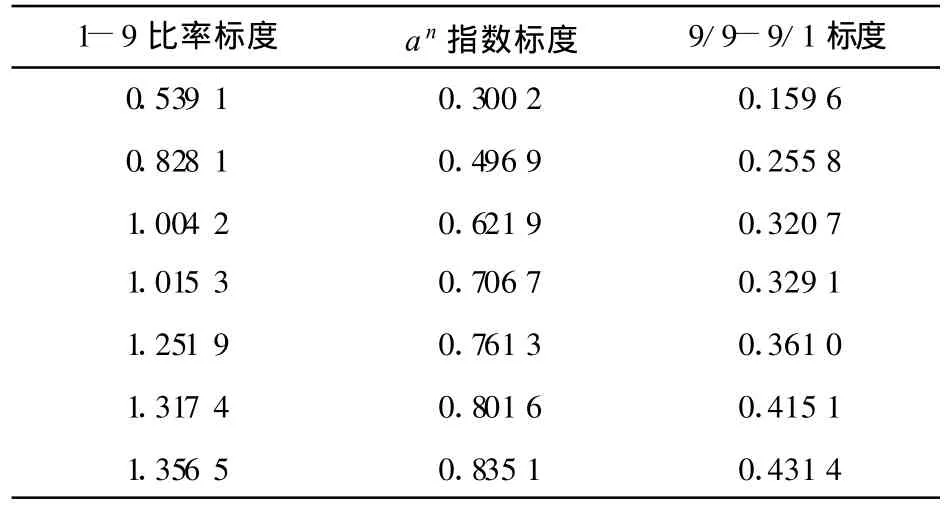
表3 3～9階判斷矩陣在不同標度系統下的RI值

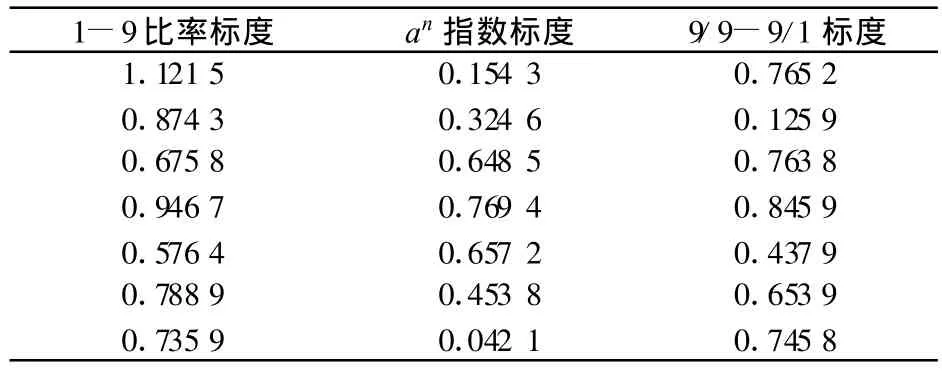
表4 3～9階判斷矩陣在不同標度系統下的CR值

大量實驗結果統計表明,在互反型標度里面,指數標度an的滿意一致性檢驗比率較其他標度的一致性檢驗比率所占比例最高,可見指數標度an比其他標度更合理,因此,在使用層次分析法進行分析時,采用指數標度會較之其他標度具有更好的一致性。

4 結束語

用數學反證的方法證明了1-9比率標度,an指數標度,9/9-9/1標度下的完全一致互不相容,并利用實驗方法得出有實際意義的結論,該分析方法雖然還存在一些誤差,但該方法對于分析提高層次分析法的準確度具有一定的實際意義。

[1]王連芬,徐樹柏.層次分析法引論[M].北京:中國人民大學出版社,1990.

[2]徐樹柏.層次分析法原理[M].天津:天津大學出版社,1988.

[3]譚躍進.定量分析方法[M].北京:中國人民大學出版社,2006.

[4]鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.

[5]杜 棟,龐慶華,吳 炎.現代綜合評價方法與案例精選[M].北京:清華大學出版社,2008.