關于二次系統極限環的分布

岳錫亭, 孫 艷

(長春工業大學基礎科學學院,吉林長春 130012)

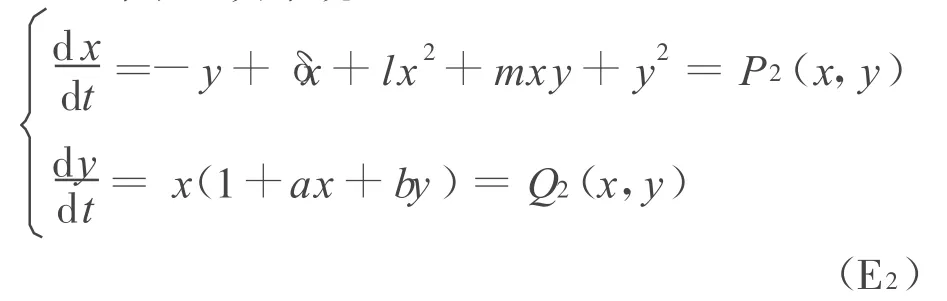
對于二次系統的極限環個數的上界及分布是人們一直關心的問題[1-3],文獻[4-5]證明了當系統(E2)的兩個奇點D(0,0),N(0,1)分別為粗焦點,且當l≥0,δ(m+δ)＞0時,系統(E2)的極限環是集中分布的。對于l＜0的情形文中給出以下定理。

定理1 δ(m+δ)+l=0時,(E2)的極限環集中分布。

證明:不妨設δ(m+δ)＞0,當δ(m+δ)+l=0時,有

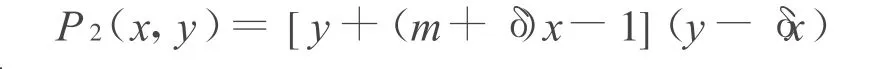
易見,奇點N(0,1)外圍的極限環不能與直線y-δ x=0相交。奇點D(0,0)外圍的極限環不能與直線y+(m+δ)x-1=0相交。假設奇點N(0,1)外圍的極限環為L,沿著N(0,1)外圍的極限環L對(E2)的發散量積分有:

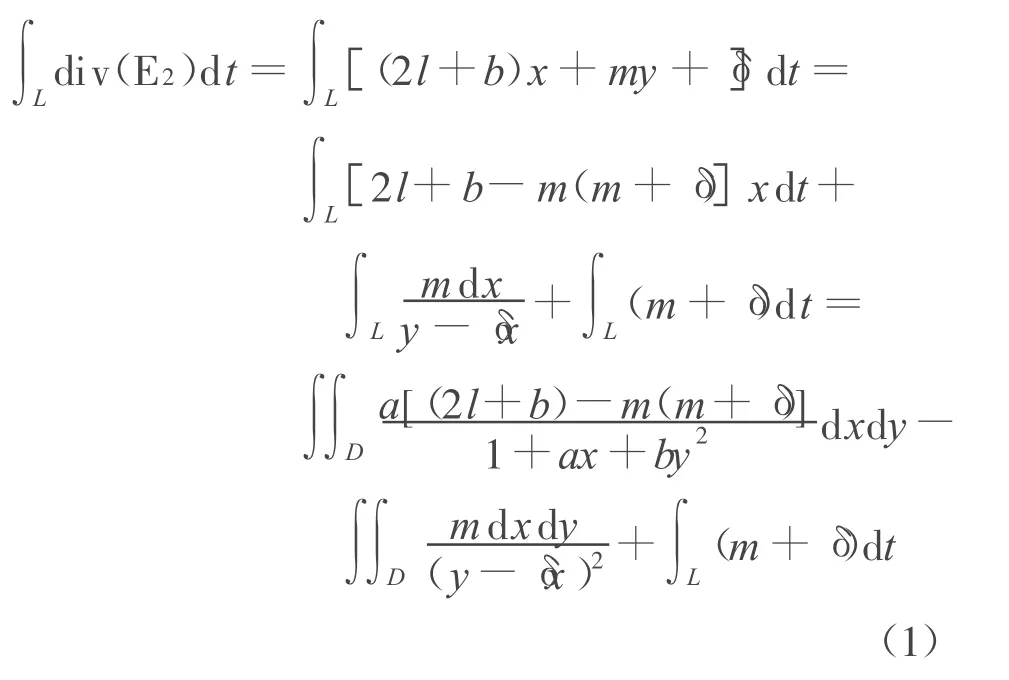
這里D是由L所圍成的區域,在應用格林定理時注意到L是順時針方向的。注意到m+δ=,當l＜0時,m+δ與δ的符號相同,且有

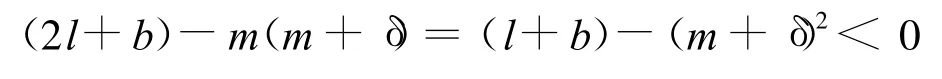
于是,當ma＞0,mδ＜0時,N(0,1)外圍無環。而對于D(0,0)外圍的極限環有

這里L的方向是逆時針方向。于是,當ma＞0,mδ≥0時,D(0,0)外圍無環。

兩者結合,當ma＞0,δ(m+δ)+l=0時,(E2)的極限環集中分布。

再由文獻[2]的引理2知,ma≤0,δ(m+δ)＞0時,(E2)的極限環集中分布知定理1成立。

定理2 當m-bδ=0,δ(m+δ)＞0時,系統(E2)的極限環集中分布。

這里依然假設N(0,1)和D(0,0)為粗焦點,且l＜0。否則由文獻[2]知(E2)的極限環集中分布。

證明:系統(E2)的極限環必然地和發散量為零的直線L:my+(2l+b)x+δ=0相交,并圍繞其交點(切觸點)于其內部,沿著系統(E2)對發散量為零的直線L求導數,得到方程為:

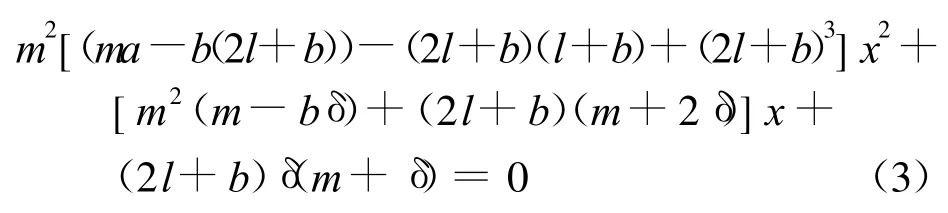
因ma＞0,所以假設ma-b(2l+b)＜0。否則由文獻[2]知其極限環為集中分布,再由m+2δ=(m+δ)+δ的符號與δ的符號相同,于是可知在式(3)中x2項的系數小于零,x項的系數的符號與-δ的符號相同。常數項的符號小于零。所以式(3)若存在根(切觸點),則兩個根的符號與δ的符號相反,又因直線L:my+(2l+b)x+δ=0與在點處相交,而是無切線。式(3)的兩個零點或同時位于直線y=的下方,或同時位于直線的上方,由此知系統(E2)的極限環為集中分布,如圖1所示。

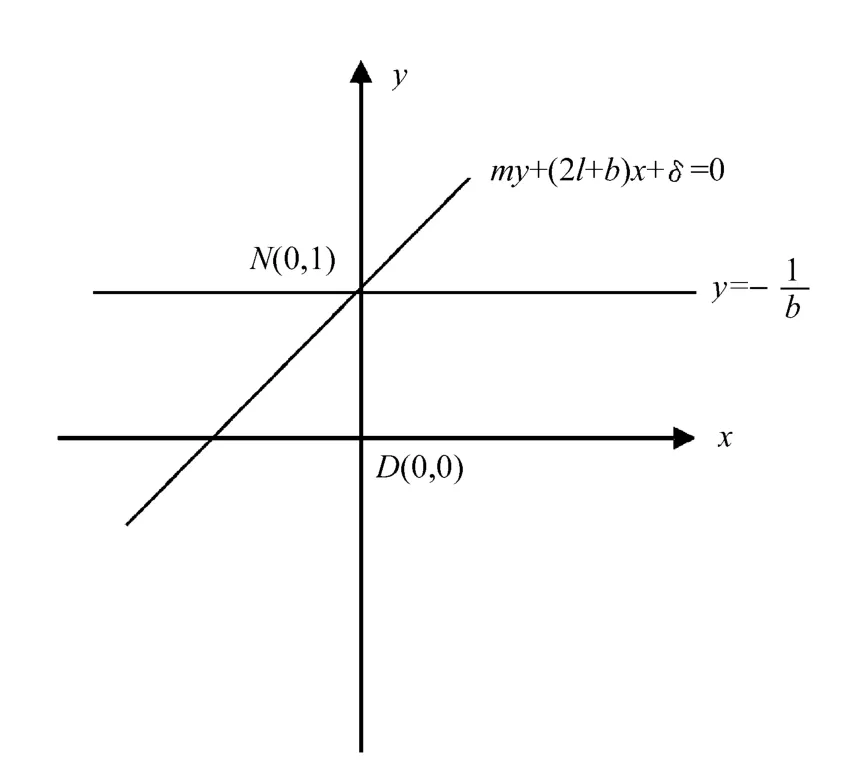
圖1 系統(E2)極限環集中分布圖

即系統(E2)的極限環只能在一個奇點外圍出現。

[1] 葉彥謙.極限環論[M].上海:上海科學技術出版社,1984.

[2] 葉彥謙.多項式微分系統定性理論[M].上海:上海科學技術出版社,1995.

[3] 岳錫亭,閆 麗.關于二次系統極限環的分布[J].東北師大學報:自然科學版,2003,35(1):18-22.

[4] 岳錫亭.一類二次多項式微分系統極限環的分布[J].長春工業大學學報:自然科學版,2002,23(4):55-57.

[5] 岳錫亭.關于二次系統極限環的分布[J].長春工業大學學報:自然科學版,2002,23(1):50-52.