低雷諾數下渦輪轉子內部流場的數值模擬研究

王如根，李 勇，曾令君

(空軍工程大學 工程學院，西安 710038)

1 引言

隨著高空飛行器應用的日益廣泛，對高空低雷諾數條件飛行下的發動機各部件特性研究越來越受到重視。要滿足高空長時間巡航的要求，除飛機本身的氣動外形需要針對高空飛行特點進行優化設計外，保證動力裝置在高空低速飛行條件下具有良好性能也是關鍵技術之一。在高空飛行時，發動機主要部件性能受雷諾數下降的影響十分嚴重，從而影響發動機的總體性能[1]。為此，本文采用數值模擬方法來研究雷諾數下降對渦輪轉子性能的影響。

2 數值方法

本文使用Numeca軟件，以Aachen軸流渦輪的轉子葉片排為研究對象進行了三維流場數值模擬。采用時間追趕的有限體積法求解三維定常的粘性雷諾時均N-S方程。空間離散采用中心差分法，時間離散采用四階龍格-庫塔法，并采用隱式殘差光順和多重網格技術來加速收斂。湍流模型采用引入AGS轉捩模型的Spalart-Allmaras湍流模型，以考慮附面層轉捩對渦輪性能的影響[2]。計算網格采用可視化IGG/AUTOGRD網格生成程序生成，為獲得較好的網格質量，在轉子葉片通道中采用了H-O-H型結構化網格，沿周向、徑向和軸向的網格節點數為25×49×201，為了盡量減小網格質量對計算精度的影響，本文生成的計算網格能保證所有網格單元內部各網格邊線的夾角均大于20°，網格長寬比不大于1 000，相鄰網格的膨脹比小于3，距固體壁面第一層網格滿足0＜y+＜5。為保證葉頂區域的網格質量，葉頂區域采用了蝶型網格。圖1給出了軸向和周向網格示意圖，圖2給出了計算網格三維視圖。

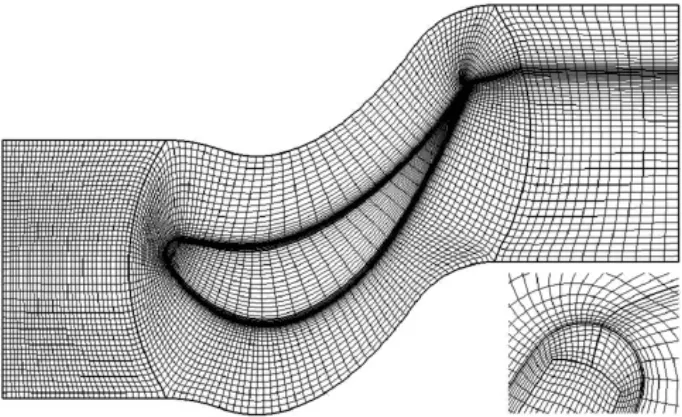
圖1 軸向和周向網格圖Fig.1 Axial and circumferential grid

圖2 計算網格三維視圖Fig.2 Three-dimensional computation grid

3 計算結果及分析

在對低雷諾數條件下的流動進行模擬之前，先進行了試驗工況條件下的模擬計算驗證。表1給出了在試驗點數值計算得到的渦輪轉子流量和出口相對馬赫數與試驗值的比較。由表中可以看出，采用加入AGS轉捩模型的S-A湍流模型計算得到的結果與試驗結果具有很好的符合性。

表1 計算值和試驗值的對比Table 1 Comparison between computation and experiment results

為分析雷諾數(雷諾數基于出口氣動參數和葉片中徑處弦長定義)變化對渦輪性能的影響，在不改變葉片、流道幾何結構的情況下，通過改變進口總溫、總壓和出口靜壓等相關參數，首先計算了地面、10 km高空和20 km高空三個不同雷諾數條件下的渦輪總體性能，并進行了分析、對比。

在100%設計換算轉速，不同雷諾數條件下渦輪轉子特性曲線如圖3所示，其中相對換算流量的定義為Wgcor/Wgcord。由圖中可見，效率和相對換算流量均隨雷諾數的降低而降低，但下降幅度有很大不同：在飛行高度H=10 km以下高度，隨著雷諾數的下降，轉子性能下降很慢，渦輪轉子的效率特性線向下移動量很小，渦輪落壓比的變化范圍有所減小(穩定工作范圍減小)，但減小范圍也很有限，相對換算流量也只有微量降低。但飛行高度超過15 km后，隨著高度的增加(雷諾數下降)，渦輪轉子的效率特性線顯著下降，渦輪落壓比變化范圍和相對換算流量也有較為明顯的降低。對比地面參考狀態(Re＝2.212×105)和H=20 km(Re＝1.910×104)的計算結果，渦輪轉子的峰值效率降低了約19%，最大換算流量降低了約5%。由此可見，雷諾數下降對渦輪轉子性能有很大的影響，將嚴重惡化渦輪轉子的工作特性。

顯然，渦輪性能的變化存在一個臨界雷諾數，當渦輪出口雷諾數高于臨界雷諾數時渦輪性能下降較慢，而當出口雷諾數低于臨界雷諾數后渦輪的性能下降很快。因此探討臨界雷諾數的大小對于分析渦輪性能隨雷諾數的變化規律是一件很有意義的工作，為此本文進一步取不同的飛行高度對應的渦輪出口雷諾數進行了大量計算。從圖3給出的結果表明：對于該渦輪轉子而言，臨界雷諾數應在7.07×104～4.30×104之間，對應的飛行高度在 H=12～15 km。

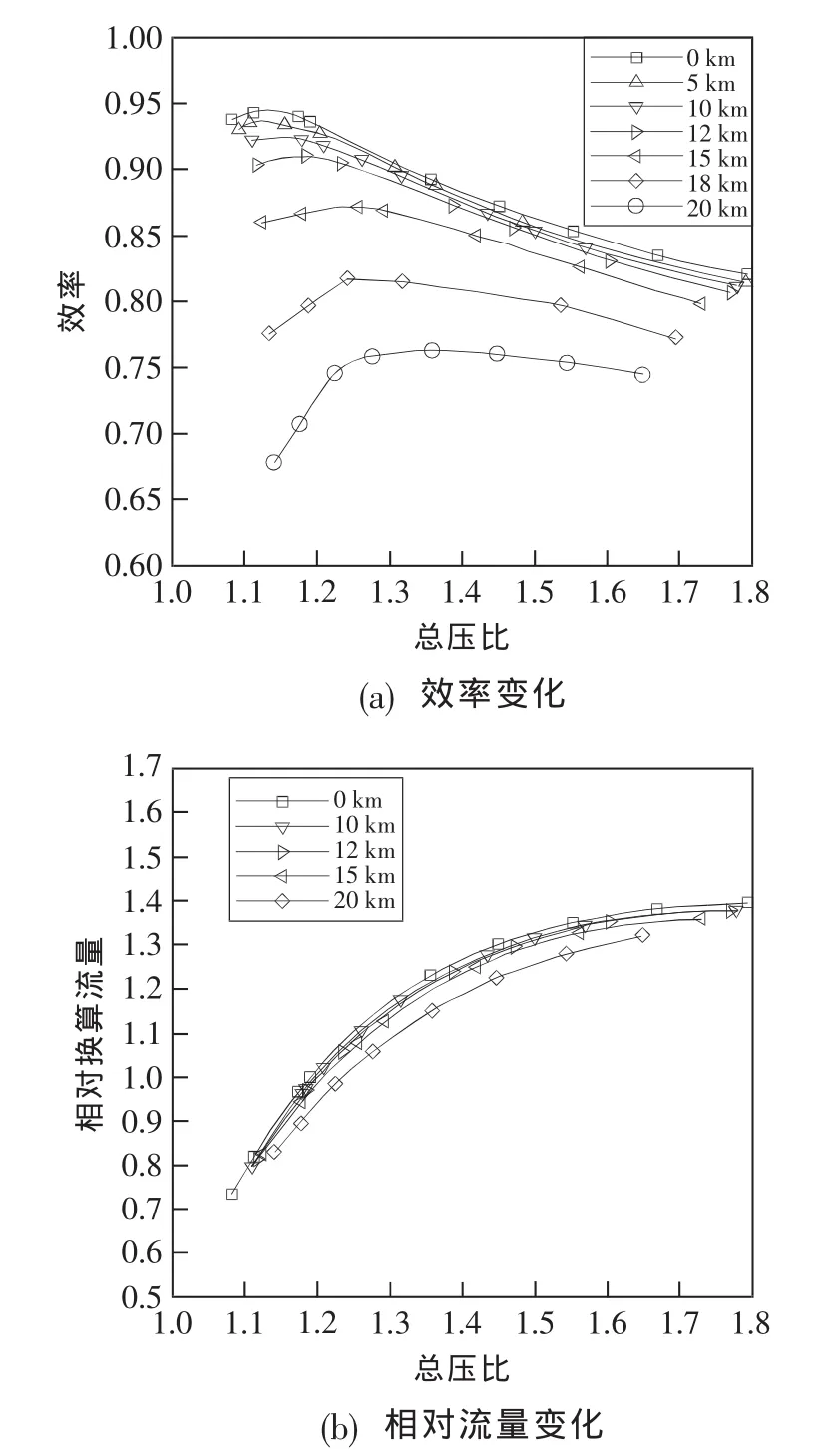
圖3 100%設計換算轉速、不同雷諾數條件下渦輪轉子特性Fig.3 Characteristics of turbine at 100%design rotation speed with different Reynolds number

為了更加細致地分析雷諾數對渦輪轉子性能帶來的影響，有必要進一步分析不同雷諾數下渦輪轉子的流場細節。本節對三種雷諾數(地面、H=10 km和H=20 km)條件下最小渦輪落壓比工作點的轉子葉片內部流場進行對比分析。不同雷諾數條件下，最小落壓比工況渦輪轉子葉片50%葉高馬赫數云圖分布如圖4所示。由圖中可見，隨著雷諾數的降低，葉片表面附面層明顯增厚，特別是在吸力面尾緣處附面層的增厚更為顯著。附面層增厚會造成葉片流動損失增加，對渦輪性能造成不利影響。

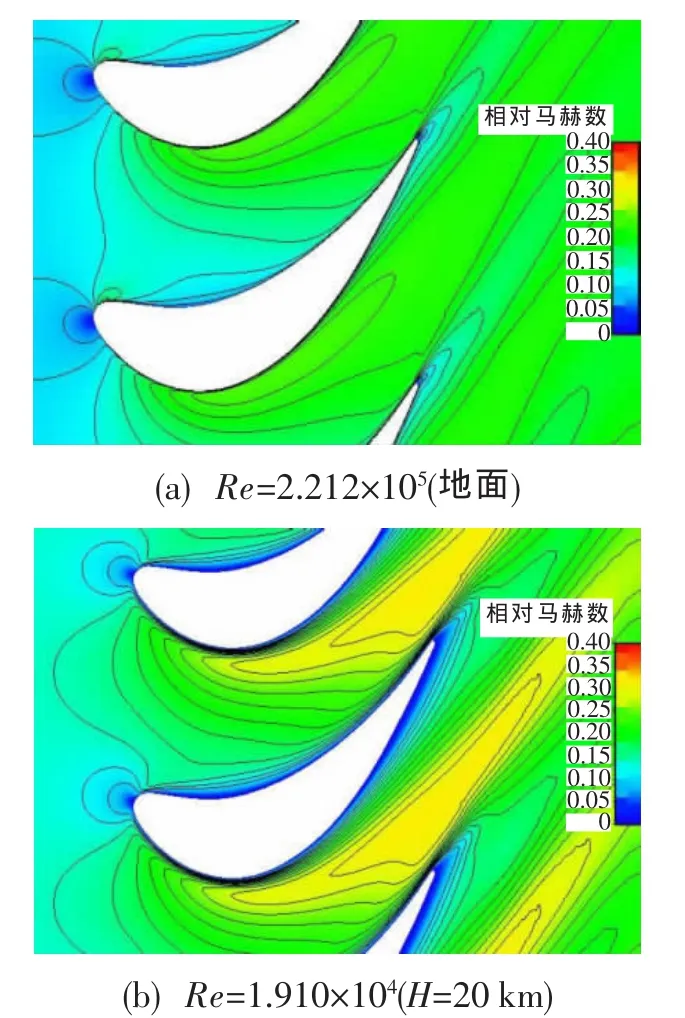
圖4 不同雷諾數條件下最低落壓比工況50%葉高相對馬赫數云圖Fig.4 Relative Mach number at 50%blade height at the lowest pressure drop ratio operation condition with different Reynolds number

圖5 進一步給出了渦輪轉子葉片不同軸向截面處的相對馬赫數云圖。由圖中可見，在高雷諾數條件下，各個截面的吸力面附面層從葉根到葉頂都很薄，僅最后一個截面的葉展中部與葉頂之間的附面層相對較厚。在低雷諾數條件下，各個截面吸力面的附面層都有所增厚，特別是最后一個截面吸力面附面層的增厚非常顯著，而且吸力面附面層沿徑向的分布極不均勻，在葉展中上部存在附面層大量堆積現象，形成了一個較大面積的低速區，減小了葉片通道的流通能力，并造成很大的損失。

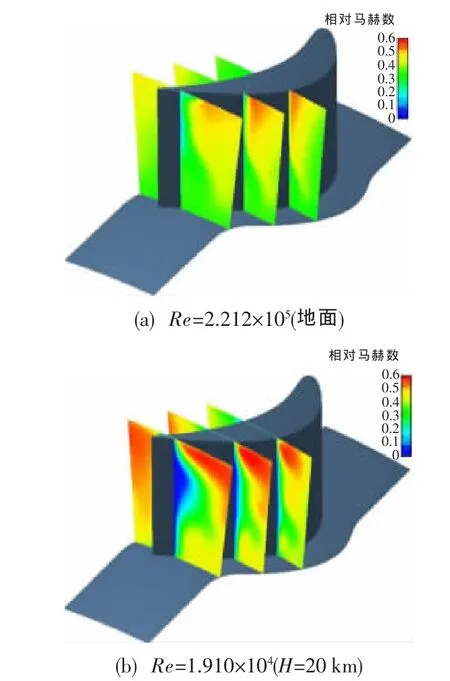
圖5 不同雷諾數條件下最低落壓比工況不同軸向截面處相對馬赫數云圖Fig.5 Distribution of relative Mach number on different axial chord at the lowest pressure drop ratio operation condition with different Reynolds number

圖6 給出了不同雷諾數條件下近峰值效率工況渦輪轉子葉片不同葉高表面壓力分布，圖中不同雷諾數下的壓力系數Cp分別利用轉子的進口總壓進行了無量綱化。由圖中可見，在低雷諾數條件下，葉片表面的壓力系數較小；同時，在低雷諾數條件下葉片表面附面層的轉捩推遲，尤其是在中部葉高以上葉片吸力面附面層轉捩的推遲尤為明顯，直到快接近葉片的尾緣才開始發生附面層的轉捩，而在高雷諾數條件下葉片吸力面附面層在中部弦長處就已經開始發生轉捩。

圖7則展示了不同雷諾數條件下96%軸向截面處的總壓損失等值線分布圖，此處總壓損失的定義為：(Pt，inlet-Pt)/Pt，inlet。 由圖中可見，隨著雷諾數的降低，該截面處的總壓損失明顯增大。在雷諾數為2.212×105條件下，損失主要集中在壓力面和吸力面的近壁區，且在吸力面與葉頂的角處有一個相對較高但范圍不大的損失區，這極有可能是由葉頂泄漏渦造成的。當雷諾數降至9.172×104時，損失有所增大，在葉展中部與葉頂之間靠近吸力面一側有一個損失明顯增大區域。當雷諾數進一步降至1.910×104時，這個區域明顯擴大，損失進一步增加，而且高損失區域明顯從葉片頂部向葉片中下部方向發展。應該說隨著雷諾數的下降，不僅僅是粘性力增強導致附面層增厚、損失增大這樣簡單，而是由于渦輪葉片通道內的流動狀態發生了很大變化從而導致渦輪效率顯著降低。為了更進一步了解導致損失增大的原因，有必要看一看葉片通道內的渦流情況。圖8為不同雷諾數條件下葉片吸力面近壁面的極限流線圖，圖中所示分離線為葉片通道內上下通道渦到達吸力面時的分離線，附著線為葉頂泄漏渦附著線[4，5]，分離線沿徑向的長度代表了通道渦的尺寸。

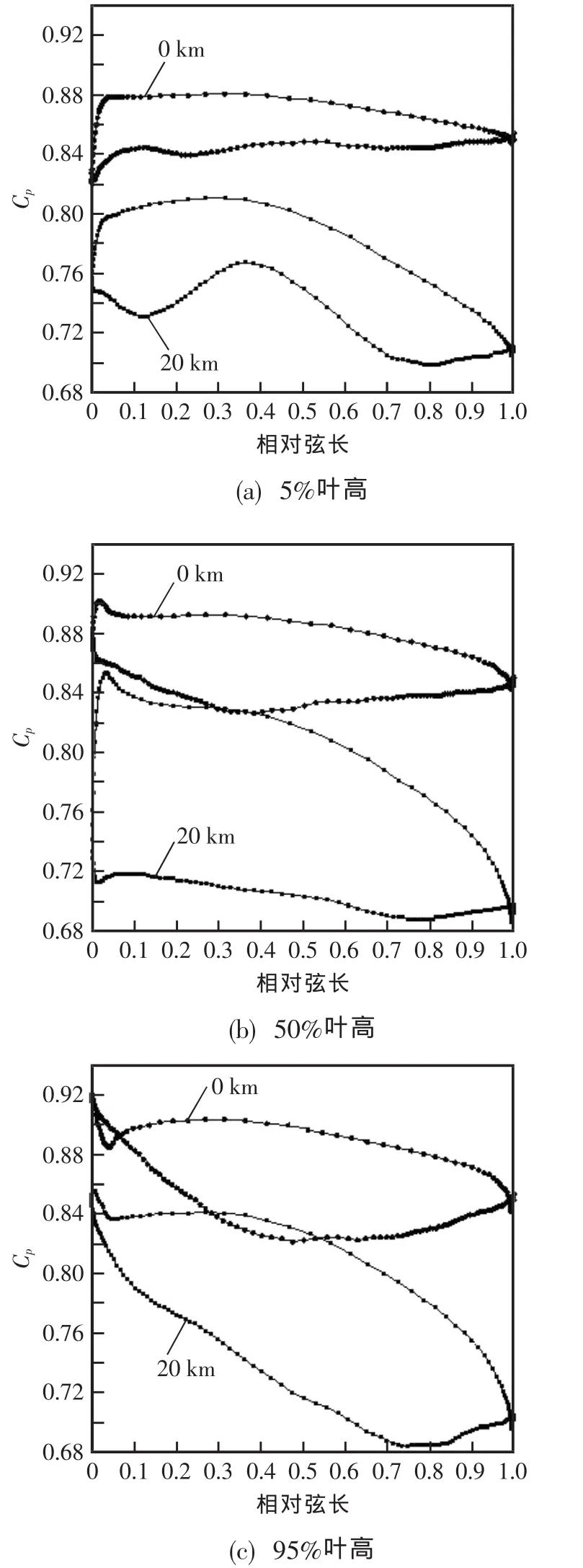
圖6 不同雷諾數條件下近峰值效率工況不同葉高葉片表面壓力分布Fig.6 Load of different blade height at close to peak efficiency operation condition with different Reynolds number

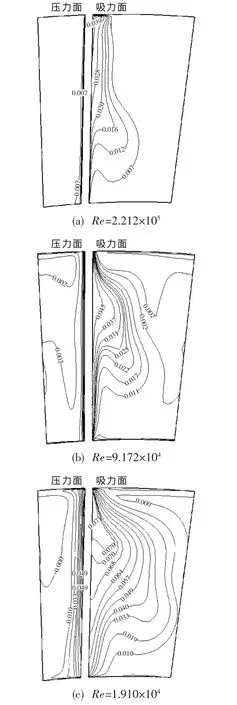
圖7 不同雷諾數條件下最低落壓比點96%軸向截面處總壓損失等值線圖Fig.7 Total pressure loss on 96%axial chord at the lowest pressure drop ratio with different Reynolds number

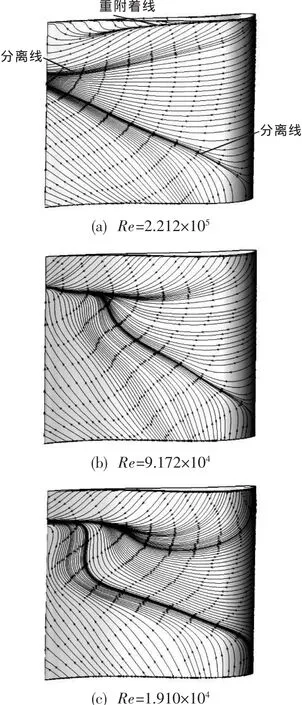
圖8 不同雷諾數條件下最低落壓比點葉片吸力面近壁面極限流線圖Fig.8 Streamline on suction surface of blade at the lowest pressure drop ratio with different Reynolds number

由圖8可見，在所有雷諾數條件下，上通道渦在葉頂泄漏渦的擠壓下均向葉根方向移動，但在離心力的作用下向下移動的位移有限；下通道渦則在離心力的作用下總有一個向上運動的趨勢，然而雷諾數不同時下通道渦的移動量并不相同。在雷諾數為2.212×105的條件下，葉片表面附面層相對較薄，離心力作用有限，因此下通道渦雖然向上運動，但并未與上通道渦相遇。當雷諾數降至9.172×104時，由于粘性作用加強，附面層厚度相應增加，上、下通道渦的強度也隨之增強，同時離心力對附面層中氣流的作用效果更為明顯，上通道渦向下移動量減少，而下通道渦向上運動的速度迅速增加，并在接近尾緣處與上通道渦相遇，上下通道渦相互摻混后一起向尾緣發展，并導致流動損失增加。當雷諾數進一步降至1.910×104時，下通道渦在向上運動的過程中遇到上通道渦的阻礙，于是在葉片吸力面尾緣中上部區域形成一個徑向渦，由于該徑向渦與主流氣流方向垂直，由此將產生大范圍的氣流分離，并引起渦輪性能迅速惡化。

綜上所述，在低雷諾數條件下，通道渦是影響葉片損失的主要因素，通道渦的增強導致損失增加，并在低于臨界雷諾數的情況下引起下通道渦的徑向運動。在通道渦的卷吸作用下，使低能流體在葉片尾緣吸力面葉展中部與葉頂之間的區域大量聚集，造成很大損失，進而對渦輪效率與穩定工作范圍造成不利影響。

4 結論

(1)雷諾數下降使渦輪性能和穩定性變差，特別是當雷諾數低于臨界雷諾數時，渦輪性能下降更為明顯。

(2)雷諾數變化對渦輪葉片表面附面層發展影響較大。在低雷諾數情況下，葉片表面附面層轉捩推遲，吸力面附面層氣流明顯增厚，導致葉片尾緣吸力面局部分離，從而影響渦輪性能和工作穩定性。

(3)隨著雷諾數的降低，渦輪內部葉柵通道的通道渦逐漸增強，特別是下通道渦隨著雷諾數的降低將在葉片尾部吸力面葉中至葉頂區域形成徑向渦，從而導致渦輪效率顯著降低。

[1]屠秋野，陳玉春，蘇三買，等.雷諾數對高空長航時無人機發動機調節計劃和性能影響[J].推進技術，2005，26(2)：125—128.

[2]Abu-Ghannam B J，Shaw R.Natural Transition of Boundary Layers-The Effect of Turbulence, Pressure Gradient, and Flow History[J].Journal of Mechanical Engineering and Science，1980，22(5)：213—228.

[3]朱光宇，俞茂錚，程代京.透平動葉柵二次流渦系演變及氣動特性的數值模擬[J].西安交通大學學報，2002，36(11)：1142—1146.

[4]王仲奇，馮國泰，王松濤，等.透平葉片中的二次流旋渦結構的研究[J].工程熱物理學報，2002，23(5)：553—556.

[5]林奇燕，鄭 群，岳國強.葉柵二次流旋渦結構與損失分析[J].航空動力學報，2007，22(9)：1518—1525.