基于GRNN網絡的燃氣輪機可靠性預測研究
曲成家,劉永葆,賀 星
(海軍工程大學 船舶與動力學院,湖北 武漢430033)
1 引言
可靠性預測是在設計階段進行定量預估未來產品可靠性的一種方法。如果說可靠性分配[1]是從系統到單元、由整體到個體來進行的話,那么可靠性預測則是按相反的方法進行。可靠性預測常常作為可靠性分配的基礎,兩者關系密切,都是可靠性設計的重要環節。
燃氣輪機的研制涉及氣動、熱力、燃燒、材料、結構、控制和機械加工等多學科技術,是知識密集、技術密集和資金密集的結晶,其可靠性是一個重要的性能指標。但由于其結構及功能復雜、啟停頻繁、運行工況多變、受環境影響大,所以依靠傳統的可靠性定量計算來衡量燃氣輪機的可靠性具有一定的局限性,甚至所得結果與實際結果相差甚遠。
運用已往的工程經驗與故障數據,結合當前的技術水平,來預測燃氣輪機實際可能達到的可靠度,即預測其在特定應用中完成規定功能的概率。這對分析評估燃氣輪機的可靠性水平、了解燃氣輪機設計和研制中的薄弱環節、指導制造廠家更好地開展設計分析和改進工作具有重要作用。
可靠性預測有許多方法,如回歸預測法、修正系數法、相似產品類比論證法等。但這些方法對帶有時序特征呈高度非線性的可靠性數據的處理,其精度往往不高。而神經網絡能實現從輸入到輸出狀態空間的高度非線性映射[2],故本文采用神經網絡來進行可靠性預測。
2 燃氣輪機可靠性預測數學模型
已知燃氣輪機在故障時間序列t1,t2,…,tn時刻的可靠性歷史統計數據,預測其下一時刻tn+1的可靠度,其數學模型可表述為[3]:

這類預測問題的關鍵是確定函數關系f,一般可用一元或多元線性回歸方法將歷史數據擬合成一個顯式表達式。此方法雖然簡單易行,但對于高度非線性問題,其擬合精度往往難以保證。而人工神經網絡卻能實現從輸入到輸出狀態空間的高度非線性映射,可用來解決上述可靠性預測問題。
在燃氣輪機的各種可靠性指標中,由于其啟動過程的復雜性、啟動程序的嚴格性,所以對其啟動可靠性有著較高的要求。根據實際運行數據,利用神經網絡較好的高度非線性映射性能,來預測和研究各型燃氣輪機的實際可靠度有著重要的意義。
為了對某型燃氣輪機實際運行的可靠性進行預測,對該型燃氣輪機啟動過程中發生的故障事件進行了統計。表1列出了前20臺次該型燃氣輪機發生啟動故障時的累計工作時間及臺次數,此前累計啟動次數為1 583次。
3 神經網絡模型及其優化設計
從神經網絡函數逼近功能這個角度來分,神經網絡可以分為全局逼近網絡和局部逼近網絡[4]。BP網絡(后傳播網絡)是全局逼近網絡的典型例子,但BP網絡對于每個樣本即輸入輸出數據對,網絡的每個連接權均需進行調整,從而導致全局逼近網絡學習速度變慢。而局部逼近網絡則只需對網絡輸入空間某個局部區域的少量連接權進行調整,從而具有學習速度快的特點。目前常用的局部逼近神經網絡有 CMAC 網絡、徑向基函數(RBF)網絡[5~8]和 B 樣條網絡等。而廣義回歸神經網絡(GRNN網絡)[9]是徑向基網絡的一種變化形式,訓練速度快,非線性映射能力強,故本文選用GRNN網絡進行燃氣輪機可靠性預測。
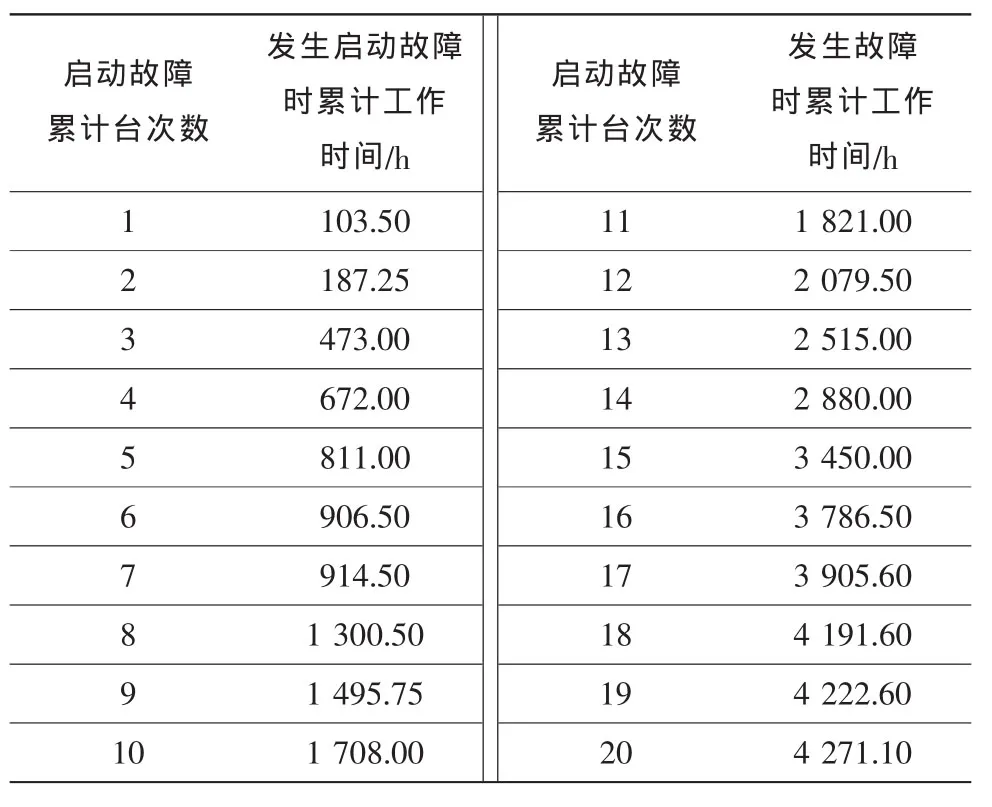
表1 某型燃氣輪機發生啟動故障時的累計工作時間及臺次數Table 1 Total operating time and number of gas turbine for starting fault
3.1 GRNN網絡基本結構與算法
GRNN網絡由一個徑向基網絡層和一個線性網絡層組成[10~12],網絡結構如圖1所示。P表示輸入向量,R表示輸入維數,Q表示每層網絡中的神經元個數,同時也表示訓練樣本的個數。
網絡的第一層為徑向基隱含層,單元個數等于訓練樣本數Q,該層的權值函數為歐幾里德距離度量函數(用‖dist‖表示),其作用是計算網絡輸入與第一層的權值IW1,1之間的距離,b1為隱含層閾值。符號“·*”表示‖dist‖的輸出與閾值b1的元素與元素之間的乘積關系,并將結果形成凈輸入n1傳送到傳遞函數。隱含層的傳遞函數為徑向基函數,常用高斯函數作為網絡的傳遞函數,式中σi決定第i個隱含層位置處基函數的形狀,σi越大則基函數越平緩,故稱為光滑因子,又被稱為分布密度SPREAD。
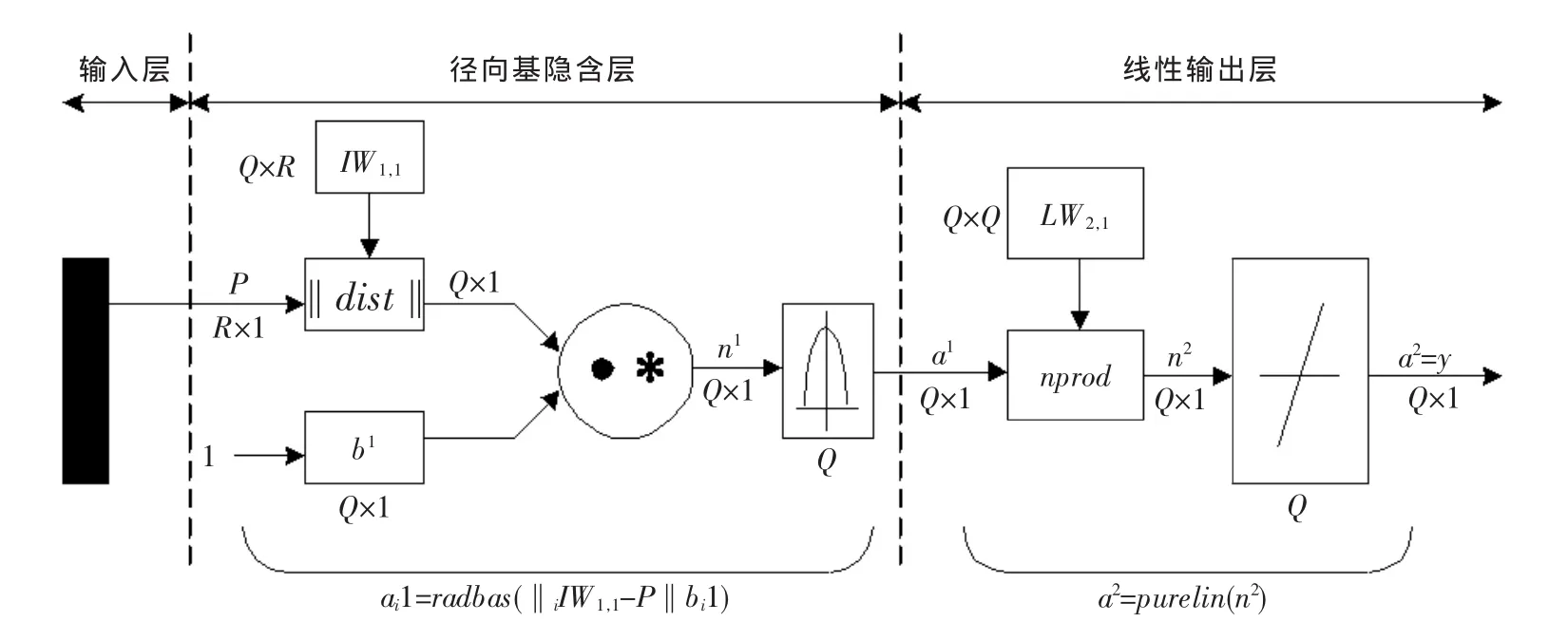
圖1 GRNN網絡結構圖Fig.1 The structure of GRNN
網絡的第二層為線性輸出層,其權函數為規范化點積權函數(用nprod表示),計算出網絡的向量n2,它的每個元素就是向量a1與權值矩陣LW2,1每行元素的點積再除以向量a1各元素之和的值,并將結果n2送入線性傳遞函數a2=purelin(n2),計算網絡輸出。
3.2 神經網絡優化設計
GRNN網絡的第一層與函數newrbe()設計網絡的原理相同,其神經元的數目與輸入期望值樣本向量對的數目相等,第一層的閾值為0.832 6/SPREAD的列向量。選擇SPREAD的原則是使得第一層輸入向量與神經元權值向量之間的距離為0.5。第一層神經元的網絡輸入為加權輸入與相應閾值的乘積,然后通過神經元函數radbas()計算得到第一層神經元的網絡輸出。GRNN網絡第二層的神經元數目同樣與輸入期望值樣本向量對的數目相等,此時其權值設定為期望值。在GRNN網絡的設計中,SPREAD越大,擬合函數就越平滑,但SPREAD的大小會影響預報誤差。所以在SPREAD的選擇上要根據平滑度和誤差來合理折中選取。
同時,為了對比,也用BP網絡進行了計算機算法實現。BP網絡設計中的關鍵就是隱層數的設計,而隱層的神經元數目選擇十分復雜,往往需要根據設計者的經驗和多次試驗來確定,因而不能用一個理想的解析式來表示。隱單元數目與問題的要求、輸入/輸出單元數目都直接相關。隱單元數目太多會導致學習時間過長、而誤差不一定最佳,也會導致容錯性差、不能識別以前沒有看到的樣本,因此存在一個最佳的隱單元數。式(2)~式(4)可用作選擇最佳隱單元數時的參考公式[13]。

式中:k為樣本數,n1為隱單元數,n為輸入單元數。如果

式中:m為輸出單元數;a為調節常數,且在1~10之間取值。

另外,結合作者的實際使用經驗,當n1在式(5)范圍內選取時可得到較佳的效果。

4 算法實現及結果分析
首先把表1中的實際數據轉換為網絡的學習樣本。根據式(1)所示預測模型對故障數據進行如下處理:以t時刻的可靠度Rt作為函數的輸出,以t時刻之前的t-1、t-2、…、t-m這m個時刻的可靠度Rt-1,Rt-2,…,Rt-m以及時刻 t作為輸入變量,構成式(6)的函數關系:

依工程實際經驗,當m取5時有較好的預測效果。根據表1中的數據,結合式(6)以及BP網絡的要求,將其轉換為BP網絡的15組訓練樣本,見表2。
其次是獲得樣本數據向量。由于其中各個指標存在相同,原始樣本中各向量的數量級差別很大,為了計算方便及防止部分神經元達到過飽和狀態,在研究中,對樣本的輸入向量中超出[-1,1]的向量進行歸一化預處理[13]。設第j列需要歸一化處理,歸一化公式為:

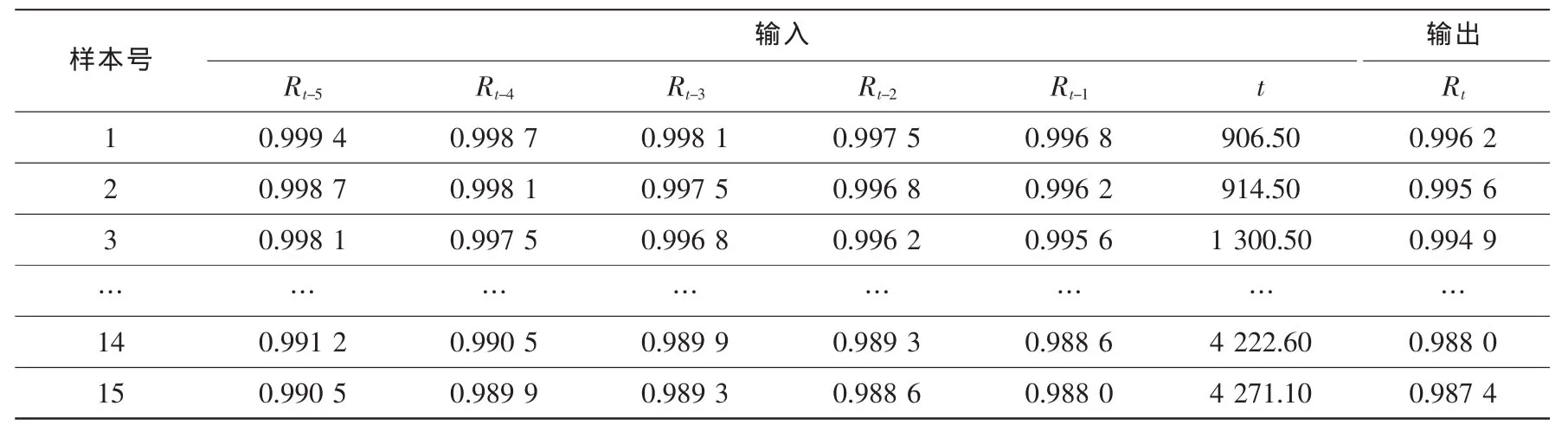
表2 網絡的學習樣本Table 2 Learning samples of neural network
本文樣本中發生啟動故障時的累計工作時間t就要進行歸一化預處理。
根據上節中闡述的神經網絡優化設計,本文分別用BP網絡和GRNN網絡進行了算法的計算機實現。為了對比各種參數對訓練結果的影響,進行了各種參數的訓練試驗,其結果見圖2~圖5。
由圖2可以看出,在本文的BP網絡設計中,隱層單元數為13時對樣本訓練100次后的誤差為1.118 59×10-11,效果比隱層單元數為3、20和35時的都要好。而文獻[3]中利用與本文相同輸入單元數的樣本訓練9 971次后誤差平方和才下降到0.005,其原因是中間層神經節點數(隱層單元數)選取過大(為 80)所致。
從圖3中可知,當SPREAD=1×10-5時,GRNN網絡在算法實現中其訓練用時比BP網絡要少,而精度要比最佳的BP網絡(隱層單元數為13)訓練100次后達到的精度要高。
從圖4中由GRNN網絡得到的預測值和真實值的比較可以看出,真實值和預測值完全重合,這是因為測試數據就是訓練數據。
圖5是根據樣本訓練好的GRNN網絡對下一時刻燃氣輪機啟動可靠性的預測。選擇對燃氣輪機將要運行到4 500 h時刻的啟動可靠度進行網絡預測模擬,結果表明,預測值為0.986 9,而參考值(即假設該時刻發生啟動失敗時的燃氣輪機可靠度)為0.986 7,預測值大于參考值,故可以認為在運行到4 500 h時刻之前,該型燃氣輪機不會發生啟動失敗故障。

圖2 BP網絡訓練誤差曲線Fig.2 The curves of training error of BP network
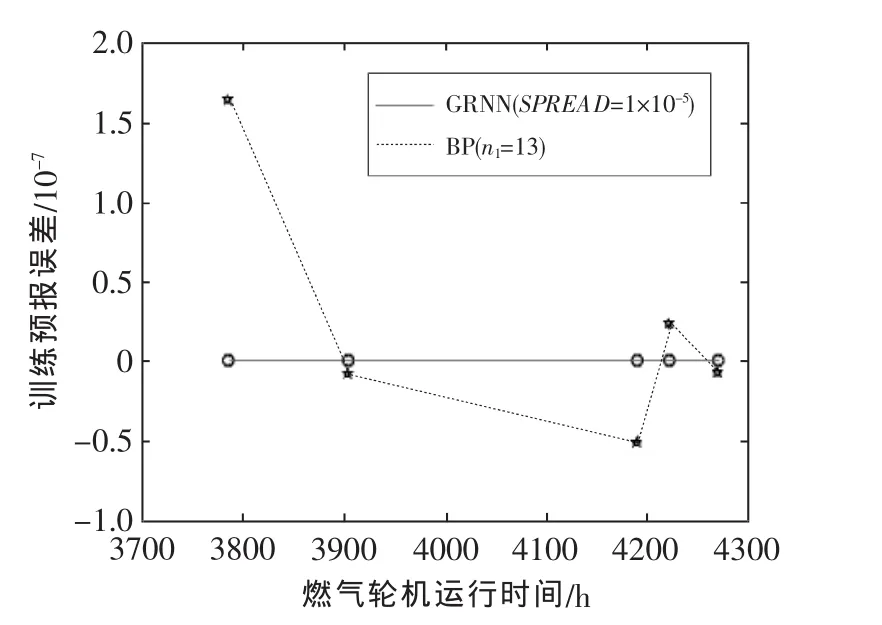
圖3 BP網絡(n1=13)和 GRNN網絡(SPREAD=1×10-5)訓練后的預報誤差對比(樣本16~20)Fig.3 Forecasting error contrast of BP(n1=13)and GRNN(SPREAD=1×10-5)after training(samples 16~20)

圖4 GRNN網絡預測值和真實值(樣本16~20)Fig.4 The sample value vs.forecasting value of GRNN(samples 16~20)
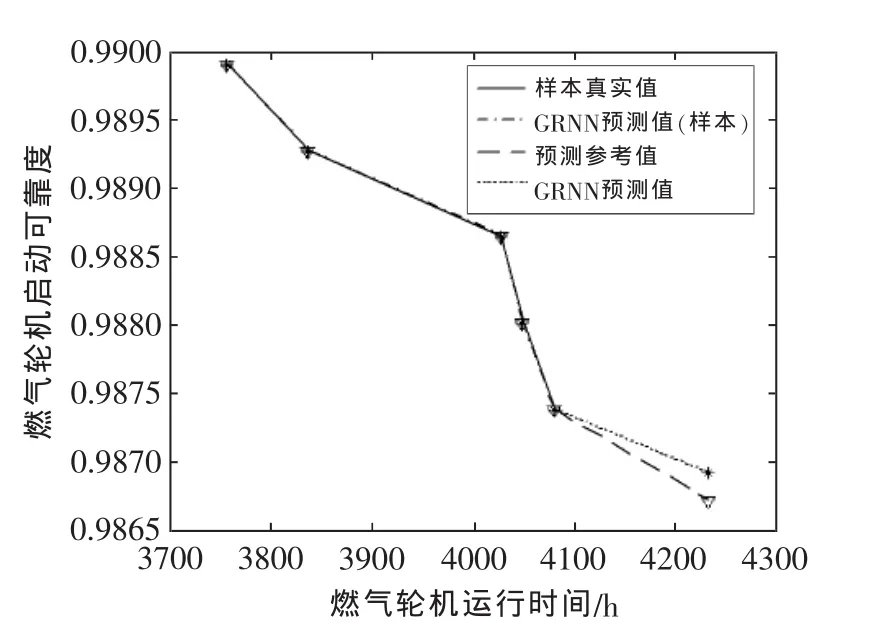
圖5 基于GRNN網絡的燃氣輪機可靠性預測Fig.5 The reliability forecasting with GRNN
5 結論
(1)利用神經網絡能夠解決高度非線性問題,顯示出其優良的逼近非線性函數的能力;而常規的回歸方法卻無能為力。所以神經網絡為燃氣輪機可靠性預測提供了一個有力的工具。
(2)無論是用BP網絡還是GRNN網絡,在算法實現中都需要采用恰當的參數才能得到較好的效果。BP網絡所需的參數設計為隱單元數,GRNN網絡所需的參數設計為其分布密度。
(3)本例中,當分布密度為1×10-5時,GRNN網絡在算法實現中的訓練用時比BP網絡的要少,而精度也要比最佳的BP網絡(隱層單元數為13)的高。
[1]王少萍.工程可靠性[M].北京:北京航空航天大學出版社,2000.
[2]Haykin S.神經網絡原理[M].葉世偉,史忠植,譯.第二版.北京:機械工業出版社,2004.
[3]吳曉平,汪 玉.艦船裝備系統綜合評估的理論與方法[M].北京:科學出版社,2007.
[4]朱大奇,史 慧.人工神經網絡原理及應用[M].北京:科學出版社,2006.
[5]Moody J,Darken C.Fast Learning in Networks of Locally-tuned Processing Units[J].Neural Computation,1989,1(2):281—294.
[6]Powell M J D.Radial Basis Function for Multivariable Interpolation[C]//.A review,IMA Conference on Algorithms for the Approximation of Functions and Data.England,1985.
[7]Broomhead D S,Lowe D.Multivariable Functional Interpolation and Adaptive Networks [J].Complex Systems,1988,2(2):321—355.
[8]Poggio T,Girosi F.Regularization Algorithms for Learning that are Equivalent to Multilayer Networks[J].Science,1990,127:978—982.
[9]Sprecht D F.A General Regression Neural Network [J].IEEE Trans Neural Networks,1991,2(6):568—576.
[10]周 昊,鄭立剛,樊建人,等.廣義回歸神經網絡在煤灰熔點預測中的應用[J].浙江大學學報(工學版),2004,38(11):1479—1482.
[11]鹿 鵬,陳曉平,趙長遂,等.高壓密相氣力輸送固相流量的實驗與GRNN網絡預測[J].熱能動力工程,2008,23(1):41—45.
[12]董長虹.Matlab神經網絡與應用[M].北京:國防工業出版社,2007.
[13]葛哲學,孫志強.神經網絡理論與MATLABR2007實現[M].北京:電子工業出版社,2007.

