新興市場股指期貨價格發現功能的研究
方 斌
(天津大學 管理學院,天津 300072)
國內外對于股指期貨推出后會對股票現貨市場的波動性產生怎樣的影響進行了大量的實證研究,由于各國的實際情況各不相同,所以至今并沒有一致的結論。2000年6月,印度國家股票交易所(NSE)推出了其指數期貨合約,NSE股指期貨的合約標的為S&P CNX Nifty指數,自該期貨合約推出以來,印度指數期貨的交易量不斷增加,雖然有時現貨指數的波動性較大,但是期貨交易所仍可保證市場的運作穩定、公平及有秩序。越來越多的投資者參與到S&P CNX Nifty指數交易中來,除了該指數本身所產生的吸引以外,更重要的原因是期貨市場的運作符合國際標準。本文將利用計量經濟學的方法對印度股指期貨價格發現功能進行初步研究,這一研究對于中國即將推出的滬深300股指期貨具有一定的借鑒作用。
1 實證方法
1.1 VAR模型
VAR是基于數據的統計性質建立模型,VAR模型把系統中每一個內生變量作為系統中所有內生變量的滯后值的函數來構造模型,從而將單變量自回歸模型推廣到由多元時間序列變量組成的“向量”自回歸模型。VAR(p)模型的數學表達式是:
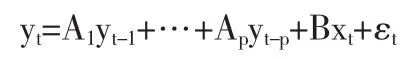
其中:yt是k維內生變量向量,xt是d維外生變量向量,p是滯后階數。k×k維矩陣A1,…,Ap和k×d維矩陣B是要被估計的系數矩陣。εt是k維擾動向量,它們相互之間可以同期相關,但不與自己的滯后值相關及不與等式右邊的變量相關。VAR模型常用于預測相互聯系的時間序列系統及分析隨機擾動對變量系統的動態沖擊,從而解釋各種經濟沖擊對經濟變量形成的影響。
1.2 非線性因果檢驗
常見的Granger因果關系是對兩個變量之間的線性因果關系做相應的檢驗,但是實際上兩個變量之間的關系還包括非線性的作用,也就是說如果兩個變量之間存在非線性的關系,那么兩個變量之間也存在因果關系。如果兩個變量x,y,存在下面的回歸式:
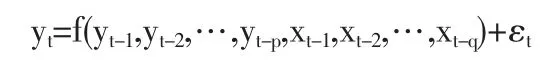
其中 εt~iid(0,σ),{xt},{yt}都是平穩的時間序列,函數 f代表兩個序列之間的一種未知關系。因為在任意的樣本空間,我們都能得到f的Taylor展開式,所以可以通過在樣本空間中的任意一點對f做線性化展開。得到下面的式子:
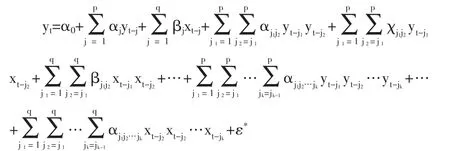
上面式子中包括了序列xt和yt滯后期的所有可能組合。對上面式子的回歸,我們采用Lasso方法。對于一般的線性回歸中,我們對變量的估計一般采用最小二乘法,Lasso方法是對最小二乘估計的一個推廣,該方法的優勢是它能使某些變量的參數快速收斂為零。實際上我們對變量做回歸的時候也希望大多數變量的系數為零,并且系數不為零的那些變量對響應變量的影響盡可能的大,對于實際問題的解釋也就更清楚明確一些。
2 數據說明
本文選取2002年8月14日至2005年12月9日印度S&P CNX Nifty股指現貨和股指期貨每日收盤價數據作為樣本數據,因為這段時間是印度金融衍生品市場中相對成熟的階段,具有較高的市場流動性。由于股指期貨與現貨市場不具有同時性,具有數據不連續的特點,同一交易日會同時有若干不同的交易價格,本文選取最近月份的期貨合約作為代表,在最近期貨合約交割后,選取下一個最近的期貨合約為代表,將不匹配的數據刪除,這樣可以得到一個連續的期貨合約序列,為防止分析過程中出現的異方差現象,以上數據均作對數處理。我們定義,CNS為S&P CNX Nifty現貨指數對數序列,CNF為S&P CNX Nifty股指期貨交易價格對數指數序列,數據來源于國泰君安證券研究所及yahoo財經網站,實證過程借助Eviews5.0軟件和R軟件。
3 實證分析
3.1 單位根檢驗
考慮到變量的非平穩性,避免模型中出現的偽回歸的問題,我們在對變量進行協整分析之前首先利用ADF檢驗法對印度股指期貨和現貨的平穩性進行檢驗,若ADF檢驗值大于臨界值,則時間序列為非平穩序列,反之則為平穩序列。對于非平穩序列,還需要檢驗其一階差分序列的平穩性,若其t階差分序列為I(0)序列(即平穩的時間序列),則此變量是t階單整的。只有變量滿足t階單整的條件下,才能進行協整分析。本文通過CNS和CNF的時間趨勢圖的觀察,可以判斷出,CNF序列和CNS序列應選擇含有截距項和具有時間趨勢項的檢驗方程進行檢驗,而通過它們的一階差分的時間序列趨勢圖的觀察,可以判斷出CNF序列和CNS序列的一階差分應該選擇具有截距項和沒有時間趨勢項的檢驗方程進行檢驗。具體檢驗結果如表1所示。
ADF的檢驗結果表明,在5%的顯著水平下,CNF和CNS的序列存在單位根,是非平穩的時間序列,而它們的一節差分序列不存在單位根,是平穩的時間序列,因此可以判斷所考察的時間序列都是1階單整的。由于各序列均為同階單整,下面我們就可以通過建立VAR模型進行協整關系檢驗。
3.2 協整檢驗
協整檢驗是從分析時間序列的非平穩性入手,尋找非平衡變量之間的長期均衡關系。常見的協整方法主要有兩變量的Engle,Grenger檢驗(簡稱EG檢驗)和多變量之間的Johanson檢驗 (簡稱JJ檢驗)。EG檢驗是基于回歸殘差的檢驗,通過建立OLS模型來檢驗其殘差的平穩性,若殘差是沒有單位根的平穩序列,則說明原序列存在協整關系。EG檢驗存在一定的缺陷,假如當協整關系的維數增加或協整的秩大于1時,EG檢驗便無能為力了。JJ檢驗是基于回歸系數的檢驗,是利用向量自回歸模型計算出與殘差矩陣相關的矩陣的特征值,根據特征值的軌跡及最大特征值進行檢驗,該方法在一定程度上糾正了EG檢驗在多變量檢驗方面的不足。本文采用Johanson檢驗法來檢驗CNF和CNS之間是否存在長期穩定的均衡關系。
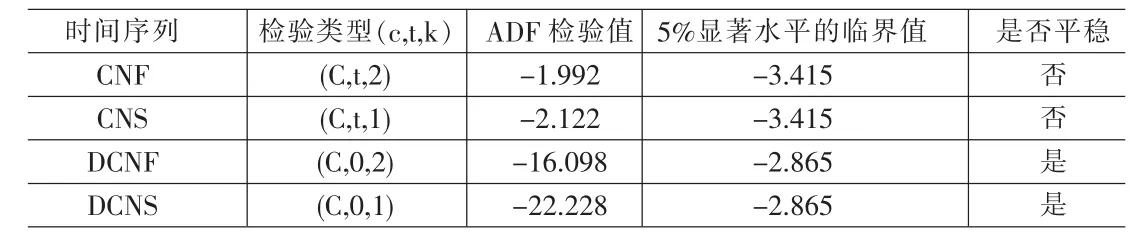
表1 ADF單位根檢驗結果
JJ檢驗的前提是建立VAR模型,建立VAR模型首先確定滯后期數k,若滯后期數k過大會導致自由度減小,直接影響模型參數估計量的有效性;若滯后期數k太小,則可能會導致誤差項自相關問題,造成參數的非一致性估計。經過反復試驗比較,滯后階數為3時,AIC和SC值最小,同時本文選擇有截距項但無確定趨勢項的VAR模型來進行協整檢驗。檢驗結果如表2所示。

表2 Johensen協整檢驗
表2表示在5%的置信水平下,CNF和CNS之間僅有一個協整關系。協整系數可以標準化,在只考慮僅有一個協整關系的假定下,經過標準化的協整系數見表3。
表3給出了估計出的標準化的協整系數,由表3可以得到CNF與CNS之間的協整方程關系式:Z=CNF-1.007×CNS+0.054。然后對Z進行單位根檢驗,可以得出Z是一個平穩的時間序列。因此,從以上分析反映了CNF和CNS之間存在一種長期的均衡關系,且長期協整方程為CNF=1.007×CNS-0.054。
3.3 誤差修正模型
誤差修正模型(ECM)的優點是既可以克服對非平穩變量做回歸時出現的偽回歸問題,又可以同時考察變量間的短期和長期關系。當變量之間存在協整關系時,可以建立ECM來進一步考察短期關系。
根據表4中的誤差修正模型1和模型2可知,模型1和模型2的誤差修正系數分別為0.3393和-0.0057,并且二者在統計上都是顯著的,說明當系統偏離均衡狀態時,下一期期貨價格和現貨價格都將對非均衡狀態進行修復。模型1中的誤差修正項系數大于0,說明誤差修正項對期貨價格的變動具有正向調整作用。模型2中的誤差修正項系數小于0,說明誤差修正項對現貨價格的變動具有負向調整作用。當短期價格偏離長期均衡狀態時,股指期貨將以33.93%的調整力度調整到新的均衡狀態,而現貨指數的調整力度僅為0.57%,因此期貨市場在長期的價格發現過程中,相對占主導地位。
3.4 非線性因果關系檢驗
下面用Lasso方法,對印度股指期貨和現貨之間的非線性因果關系進行檢驗。做滯后期為2的非線性因果檢驗,首先做現貨價格對期貨價格的因果關系檢驗。用Lasso方法得出的結果如下所示:從1到10的變量分別如下:

其中y代表期貨價格,x代表現貨價格。對于每一步計算的值如表5。
從Cp值可以看到在第5步的時候其值達到最小,則我們截取第5步的結果,這樣分別選入的變量就有變量1(yt-1),變量 8(yt-1,xt-2),變量 4(xt-2),變量 3(xt-1)以及變量 2(yt-2)。并且我們得到在第5步的時候其R2值為0.9907954,可見回歸的效果是很好的。這樣,我們就可以通過現貨和期貨的滯后一期和二期,以及現貨和期貨之間的交叉關系得出對期貨的回歸關系,也就說明了現貨對期貨具有非線性因果關系。
同樣,我們可以做對現貨價格的Lasso回歸。從1到10的變量設置分別為:
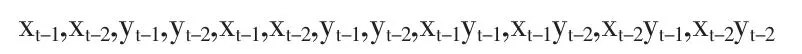
其中x代表現貨價格,y代表期貨價格。對于每一步計算的Cp值如表6。
從計算得出的Cp值可以看出,在第18的時候其值最小,所以我們截取18步的回歸。而選入變量的結果可以通過上面Lasso的步驟過程得出,最后選入的變量為:變量1,變量2,變量 3,變量 4,變量 5,變量 6,變量 8和變量 9。同時也可以得到最后回歸的R2值為0.9961607,可見回歸效果還是比較滿意的。這樣可以得到期貨同樣是現貨的非線性因果關系。

表5
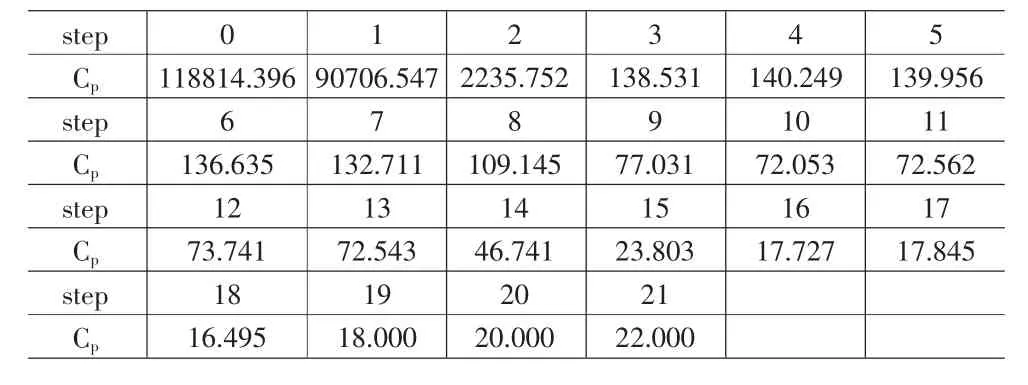
表6
4 結論
(1)VAR和協整檢驗的結果表明,短期內印度S&P CNX Nifty指數與期貨指數之間可能出現偏差,但長期來說,印度現貨指數與期貨之間存在著長期穩定的相關關系,這種長期穩定的相關關系是對股指期貨和現貨的之間規律的一種定量的描述。
(2)通過VEC模型的檢驗,揭示了印度股指期貨和現貨之間從短期偏離到長期均衡的過程,DCNS模型中的誤差修正系數相對較小,而DCNF模型中的誤差修正系數相對較大,說明現貨價格回復到均衡狀態的速度相對較慢,即主要是通過期貨價格的調整來完成,從而期貨市場在價格發現功能中處于主導地位。
(3)從非線性因果關系的結果可以看出,現貨價格對期貨價格的因果關系中R2值為0.9907954,同樣期貨價格對現貨價格的因果關系中R2值為0.9961607,說明二者相互擬合的效果都很好。也就是說印度S&P CNX Nifty指數和期貨指數之間存在雙向因果關系,即期貨指數的變動影響到現貨指數的變動,同時現貨指數的變動也影響期貨指數的變動,期貨市場和現貨市場之間的影響是相互的。
(4)印度指數期貨成功的經驗,可以為國內推出股指期貨提供一些借鑒。一個金融期貨產品的成功與否,取決于很多因素,其中穩定、成熟和高流通量的現貨市場是發展股指期貨的先決條件,也是股指期貨市場發揮價格發現功能的基礎,無論股指期貨的推出還是風險的防范與監管都要考慮到現貨市場的發展。
[1]陸樊祖.高等時間序列經濟計量學[M].上海:上海人民出版社,1999.
[2]高鐵梅.計量分析方法與建模[M].北京:清華大學出版社,2006.
[3]張曉峒.計量經濟分析[M].北京:經濟科學出版社,2006.
[4]Anne Peguin-Feissolle,Timo Terasvirta.A General Framework for Testing the General Noncausality Hypothese[C].SSE/EFI Working Paper Series in Economics and Finance,1999.

