基于MRF高斯混合模型的海浪紋理背景目標區域分割

張子丹

(上海海事大學商船學院，上海 200135)

0 引言

海平面背景下的目標區域分割是機器視覺研究中的難點，其主要原因是動態海平面背景和光照使分割出來的前景目標含有大量噪聲.另外，海浪劇烈波動引起的相機晃動也會影響目標檢測的精度.因此，建立高魯棒性背景模型是提高動態背景下的目標區域分割的關鍵.目前較為經典的背景模型有自適應平滑模型［1]、多分辨率多尺度自回歸(multiscale autoregressive)模型［2]、高斯模型［3-4]、非參數模型［5]以及卡爾曼預測模型等.上述模型能解決某些特殊場景的目標區域分割，但對于復雜海面背景有一定的局限性，如僅考慮背景的亮度信息，而很少考慮豐富的海浪紋理信息等.本文介紹1種根據海平面背景特點和海浪紋理信息建立的馬爾科夫高斯混合模型［6-8]，通過獲取圖像特征，并假設圖像特征遵守正態分布，將分割問題轉化為紋理圖像的聚類問題，從而分割出海浪紋理背景下的目標區域.

1 海平面特征分析

1.1 海浪紋理分析

由于海浪受環境(風速、光照等)影響而引起的海面變化，反映在二維圖像中為亮度和顏色的變化，微視覺模式［9]在海浪紋理中重復出現，因此，海平面波浪紋理區呈現隨機排列的多樣模式，區別于結構性較強的周期紋理，見圖1.

圖1 不同特征的海浪紋理圖像

海浪紋理分析主要借助紋理基元，圖2為不同場景下的海浪紋理基元特點.

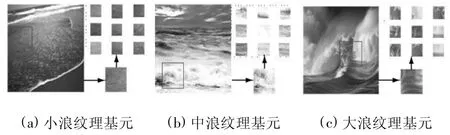
圖2 不同場景下海浪紋理基元比較

圖2 (a)為微浪紋理，其基元紋理呈現細小紋理特征，但紋理排列未呈現周期性，因此，該場景下的海浪紋理屬微紋理［5];圖2(b)為中浪紋理，其紋理更不規律，紋理基元較大;圖2(c)為大風浪場景下的紋理，其紋理基元更大，基元間的內在運動關系更難以描述.因此，僅依靠基元特性和像素灰度信息分析海浪紋理遠遠不夠，可考慮充分利用紋理的空間布局和統計方法描述海浪紋理.

1.2 海浪紋理背景的高斯模型

可見光下海浪的灰度和顏色內在的相互作用形成海浪紋理圖像，圖3為可見光下的海浪紋理圖像及其直方圖.由圖3(a)可知，海浪細致紋理圖像像素符合多態正態分布;在圖3(b)輕浪背景下，海浪開始破碎，呈現較多的反射棱角，因此，直方圖分布變得較不規則;在圖3(c)中，海浪紋理更不規則，直方圖分布更復雜，像素的分布已不符合正態分布.因此，本文根據單模態的思想用多模態思想描述復雜場景中像素點值的變化.［10]

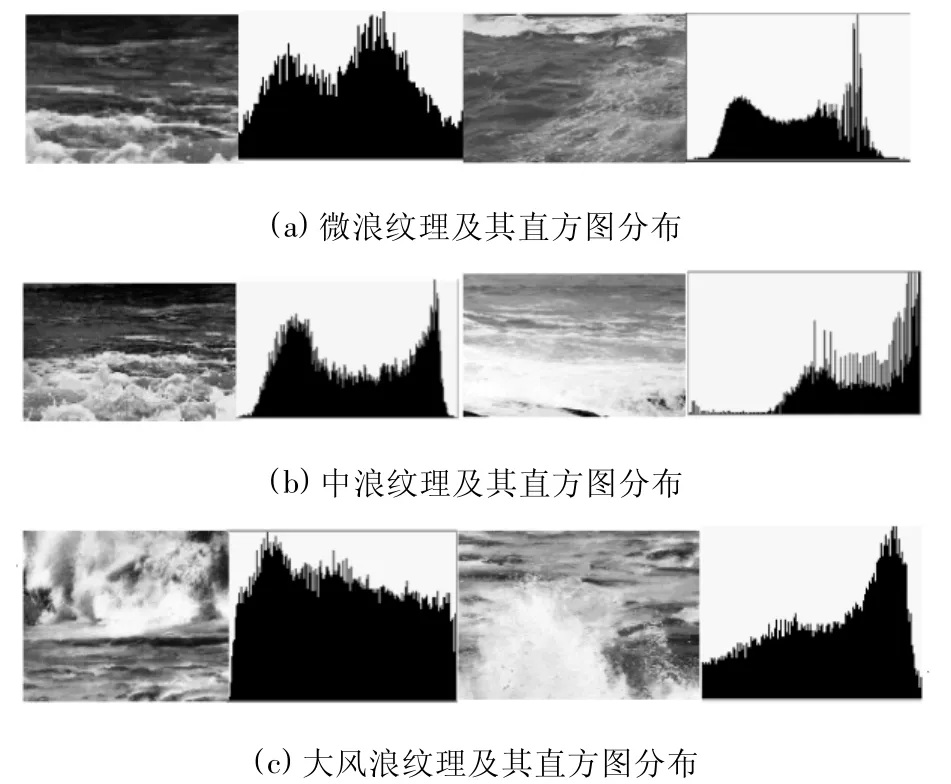
圖3 海平面背景的直方圖分布

2 MRF高斯混合模型

馬爾科夫隨機場(Markov Random Field，MRF)模型因其能充分利用空間的信息而廣泛應用于紋理分析和模糊聚類，被認為是描述圖像像素聯合概率分布的有力工具.從隨機場的觀點看，海面目標的檢測問題可看作分類問題，即如何從觀測到的灰度圖像中獲取圖像真實類別的標記圖像.

2.1 MRF和Gibbs分布

設二維m×n平面圖像像素點集合為S={1，2，…，m ×n}，K={1，2，…，Q}為像素的標記集合，Q為類別數.圖像分割就是對圖像上的每個像素分配1個像素標記集合K中的1個類別v，標記圖像為分割后的結果，表示為

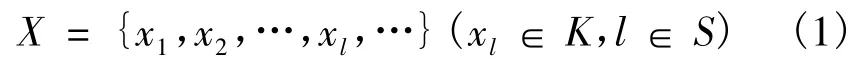
可將Y定義為S上的1個MRF.

設圖像某像素點r的鄰域為ηr(r?ηr)，S上的鄰域系統集合 η ={ηr，r∈S}.如果?v∈K，r∈S，則像素點r在其鄰域ηr中被賦予標記v的概率為P(yr=v|yηr)=P(v)，表示為1個 MRF實現，表示某像素點僅與其鄰域系統有關，與鄰域系統外的點無關.由于MRF和Gibbs分布的一致性，P(Y)可表示為

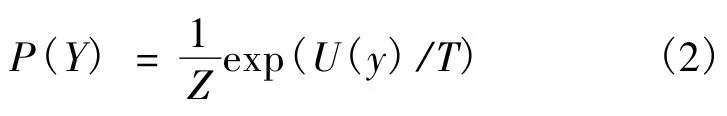
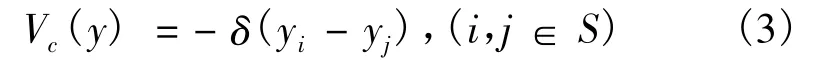
像素組 C={(i，q)，i∈S，q∈η}，η 為像素點 q 的鄰域系統;β為分割因子，U(y)值越小，實現Y的能量越小，越可能實現.

根據MRF與Gibbs分布的一致性，通過能量函數確定MRF的條件概率，從而使其在全局上具有一致性.通過單個像素及其領域的局部交互，MRF模型可獲得復雜的全局行為，即計算局部的Gibbs分布可得到全局的統計結果.

2.2 基于海浪紋理的MRF高斯混合模型

已知所觀測的輸入灰度紋理圖像Y是定義在網格集合S上的，由貝葉斯公式得

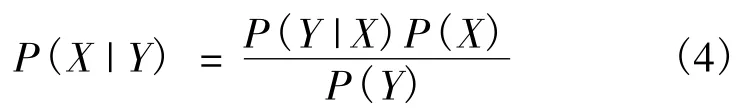
式中:P(X|Y)為后驗概率;P(Y|X)為Y的條件概率;P(X)為先驗Gibbs分布概率.目標的分割就是給定1個特定的y(y是Y的1個實現)，在某種最優準則條件下求得X的1個估計，即求使P(Y|X)最大的分割標記:

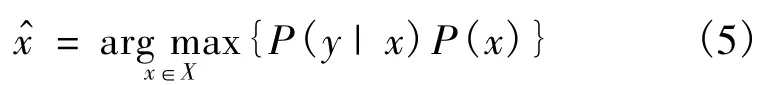
式中:x和y分別為X和Y的樣本.假設Y中的每個灰度信息 yr(r∈S)符合高斯分布，參數 θr=(μr，σv)，v=xr(r∈S)，則

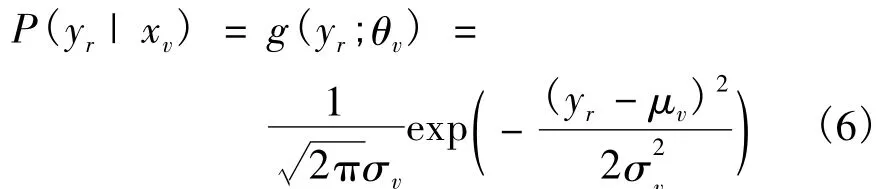
由MRF高斯混合模型表達式可得變量X和Y的聯合似然概率P(X，Y)=P(Y|X)P(X)，聯合概率可進一步表示為

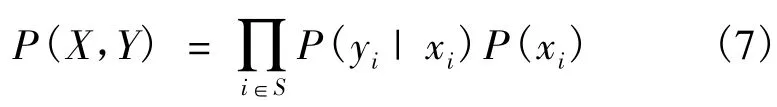
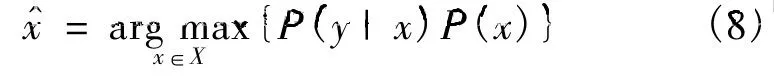
由于y分布獨立，變量x和y的聯合似然概率為

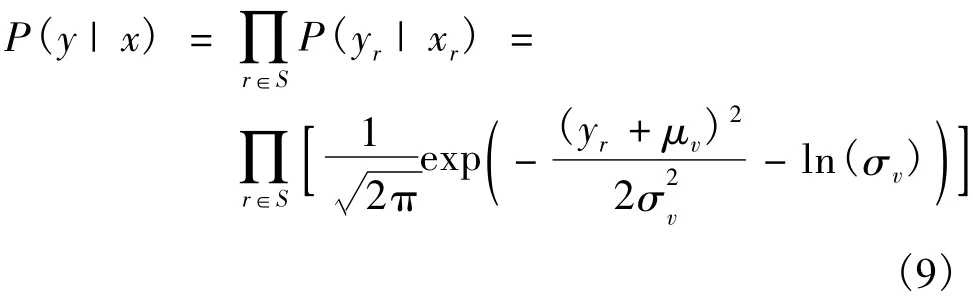
由文獻［9]可知，最優化概率估計問題可轉化為能量最小化問題

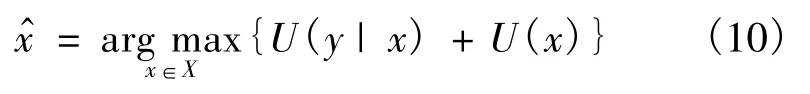
3 參數估計以及算法步驟

由上述可知，最優化概率估計問題可轉化為能量最小化問題，能量最小化問題可轉化為求式(8)的最優解問題.由于能量函數U(y|x)為非凸函數，其極小值較多，在類別不定時，不可能通過窮盡的搜索方式得到最優解.圖像邊界信息的存在以及參數和類標記的相互獨立性，使觀察數據不完備，因此，選擇EM算法［11]從不完備的數據集合里提取參數.設 y～為估計所丟失的數據，則{y～，y}為完備的數據集.通過最大化完全數據對數估計E(log P(x，y|θ))估計新的參數集合θ，再經過E-step和M-step，參數的集合可表示為

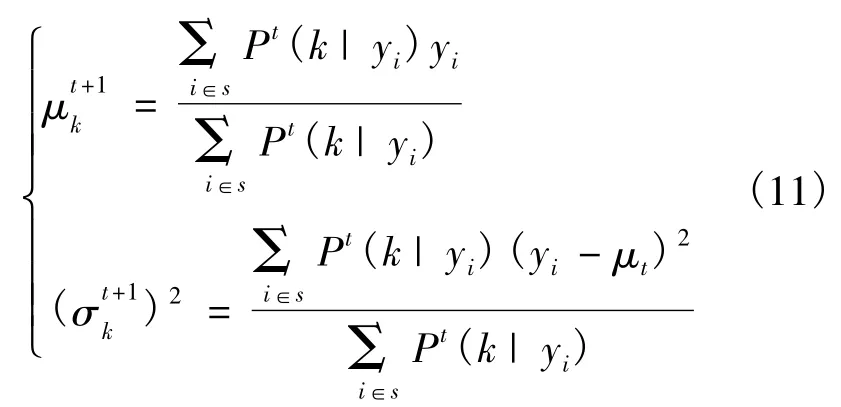
式中:t為迭代次數.

EM算法可簡單描述如下:

BEGIN

輸入圖像

步驟0 7×7中值濾波;

步驟1 初始化參數和分割參數以及迭代條件;

步驟2 E-step，用式(5)和(7)，計算 U(x|y)，U(x)，θ，計算后驗概率分布Pt(k|yi);

步驟3 M-step，極大化t時刻的期望值，更新t時刻的參數;

步驟4 執行以上步驟，滿足迭代條件則停止;

步驟5 中值濾波以及形態學處理.

輸出圖像

END

4 試驗分析

為驗證方法的可行性，可對不同紋理下的海浪紋理進行分析.所測試的圖片來自網絡和課題組，目標是將彩色圖像轉換為灰度圖像.圖像的背景為較寬廣的水域，因此，設分割類別K=2，分別表示海面背景和船艦目標(以及部分天空背景).由于分割光滑因子β值的選取沒有較好的估計模型，試驗中的β值均是在反復比較的情況下得到的.為得到較為理想的分割效果，對圖像組首先進行中值濾波.由于基于迭代的EM算法對初始值的要求較為敏感，試驗中的均值μ0取樣本的均值向量.

表1為樣本集合的部分訓練參數，從中選擇較合適的參數作為初始化參數.表1中的object表示圖像集合中的船舶集合和落水人員等小目標集合;background表示海浪細致紋理背景模型集合.

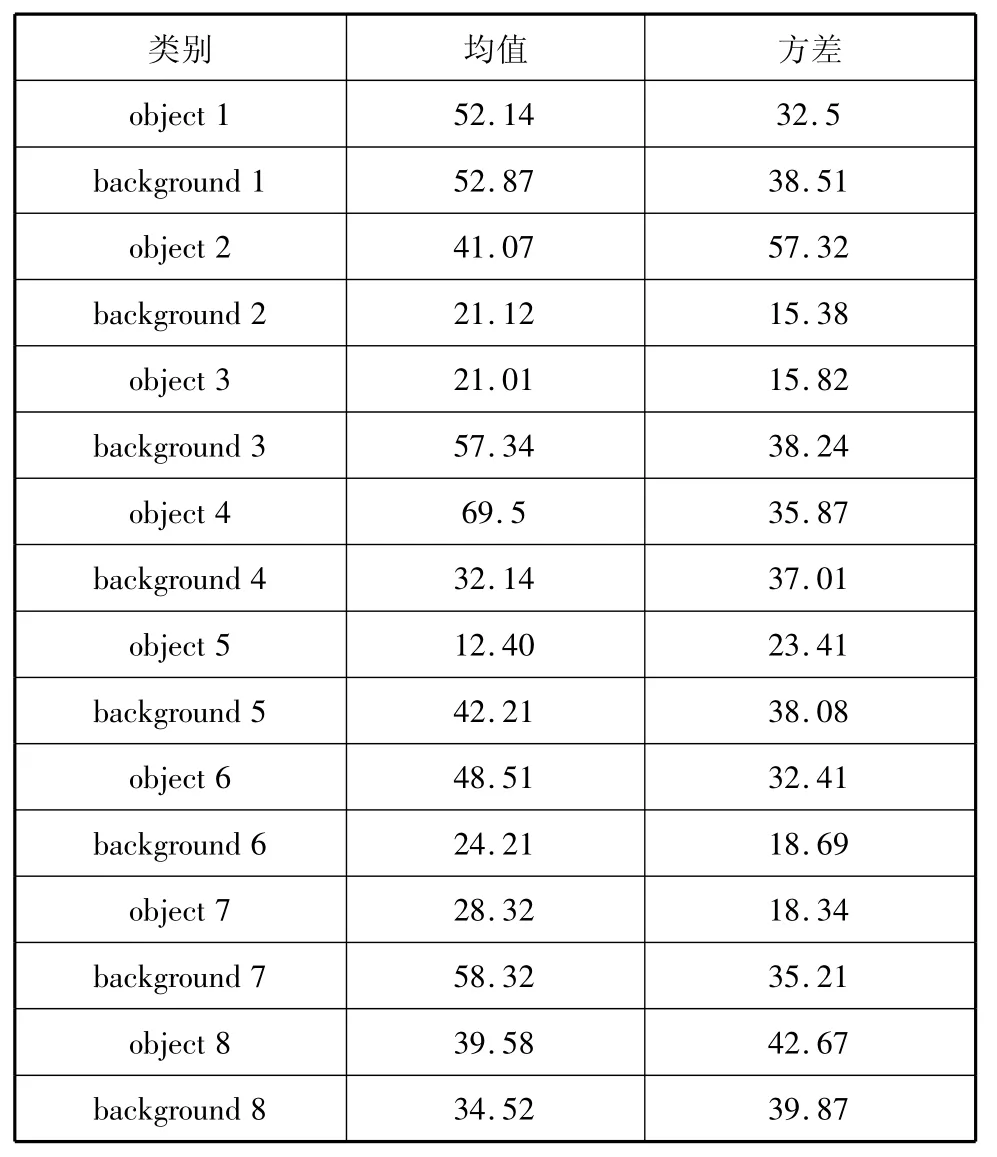
表1 樣本集合的部分訓練參數

由于參數β過大會造成細節的丟失，太小會使鄰域信息變弱，難以有效濾除噪聲，本文通過多次選擇確定β大小.由于微浪紋理較細，為控制分割光滑程度，分割因子β選擇0.4.

為表示該算法的可行性，選擇幾個經典的紋理分割方法與本文方法作比較.圖4為經典的圖像分割方法和本方法的比較，其中:圖4(a)為較細海浪紋理背景下的原始圖像，圖像場景為對比度較小且受到光照影響的海面背景;圖4(b)為GS(Gibbs-Sampler)方法得到結果;圖4(c)為基于區域生長和邊界信息的分割結果，區域生長方法未能充分利用海浪的空間分布信息而產生過分割問題;圖4(d)為改進的OSCU方法［12]，基于直方圖的自動閾值選取對于受光照影響較大的海面背景目標區域分割有局限性;圖4(e)為本文的試驗結果，較前面的幾種方法有更好的分割效果，基本能將目標分割出來，并且背景沒有過多地被劃分到目標區域中.

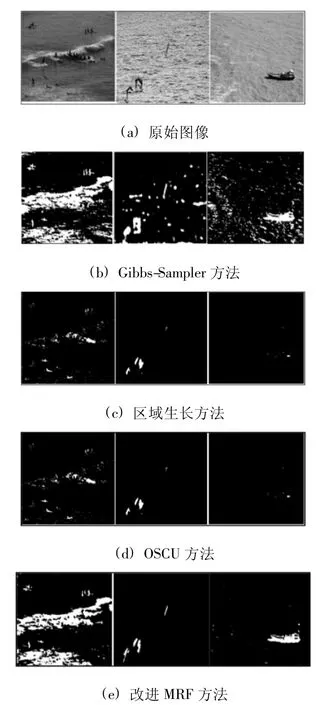
圖4 紋理分割效果對比

為表現本文方法的有效性，用分割正確率(Correct Classification Ratio，CCR)表示分割效果:

式中:C為分割正確率;Nc為分類正確的像素個數，Nt為像素總個數.表2給出各種方法的分割正確率，由表2可知本文方法的分割正確率較其他方法有較大的改進.

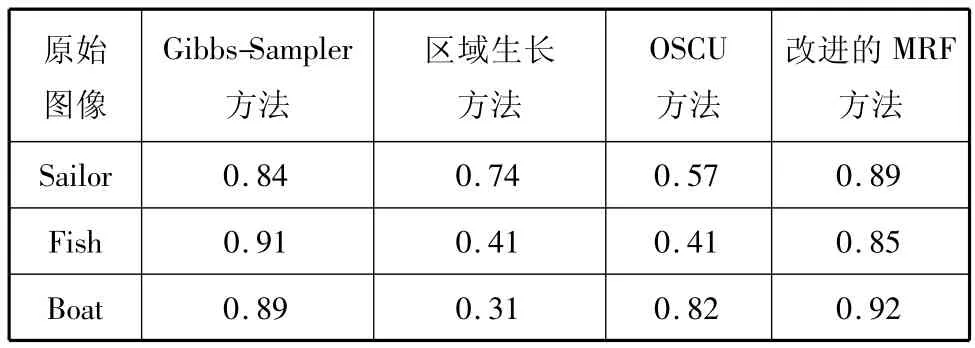
表2 不同方法的圖像正確分割率

圖5給出算法的時間比較，由算法收斂的抽樣點得到.文獻［12]的OSCU方法因其較為簡單，沒有大量的迭代運算，快于其他算法;本文算法(改進的MRF方法)雖含有大量迭代運算，但初值取得較為合理，因此算法時間符合要求;基于區域生長和邊界分割方法(區域生長方法)由于最初的數據量有限，收斂速度與其他方法相差不多，但隨著數據量的增加，收斂性受到較大限制，該算法的時間逐漸增加;GS方法(Gibbs-Sampler方法)雖然有較好的分割效果，但需要進行較多的浮點運算，且要花費較多的時間尋求全局的最優化，算法的實時性較差.

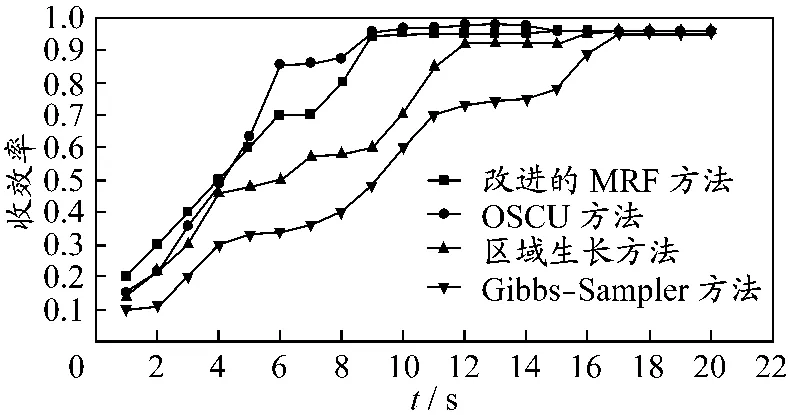
圖5 本文算法和傳統算法的時間比較

5 結束語

海浪紋理背景下的目標區域分割與傳統的場景分割有很大的不同，需要結合海浪的內在紋理形成機制和背景像素的空間分部信息進行分割.本文結合像素空間分布信息以及統計思想提出1種基于MRF高斯混合模型的海浪紋理背景目標區域分割方法.試驗結果表明該算法對細海浪紋理分割有可行性，但同時還存在著若干問題，如對于大浪和中浪背景紋理，本方法的分割精確度較低，對于天空背景和地岸等多類別的背景會造成誤分割或過分割，需進一步解決和討論.

［1]LONG W.Stationary background generation:an alternative to the difference of two images［J].Pattern Recognition，1990，23(12):1351-1359.

［2]FRAKC A.Internal multi-scale auto-regression process，stochastic realization ＆ covariance estimation［D].Cambridge，Massachusetts:MIT，1999.

［3]SCAUFFER C，GRIMSON W.Learning patterns of activity using real-time cracking［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，2000，22(8):747-757.

［4]COLLINS R，LIPTON A，KANADE T，et al.A system for video surveillance＆ monitoring［C]//8th Int Topical Meeting Robotic＆ Remote Systems，1999:510-514.

［5]ELGAMMAL A.Non-parametric model for background subtraction［C]//Eur Conf on Comput Vision.London:Springer-Verlag.2000:751-767.

［6]DENG Huawu，CLAUSI D A.Gaussian MRF rotation-invariance features for image［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，2004，26(7):951-955.

［7]KASHYAP R L，KHOTANZAD A.A model-based method of rotation invariance texture classification［J].IEEE Trans on Pattern Anal＆ Machine Intelligence，1986，8(4):472-481.

［8]DENG Huawu，CLAUSI D A.Advanced Gaussian MRF rotation invariance texture features for classification of remote sensing imagery［C]//Proc 2003 IEEE Comput Soc Conf on Comput Vision＆ Pattern Recognition.Madison，Wisconsin，2003:42-48.

［9]ZHANG Yongyue，SMITH S，BRADY M.Segmentation of brain MR images through a hidden Markov random field model and the EM algorithm［J].IEEE Trans on Med Imaging，2001，20(1):46-51.

［10]GEMAN S，GEMAN D.Stochastic relaxation，Gibbs distributions ＆ the Bayesian restoration of images［J].IEEE Trans on Pattern Anal＆Machine Intelligence，1984，6(2):721-741.

［11]HALL N R，HALL D，NASCIMENTO J，et al.Comparison of target detection algorithm using adaptive background models［C]//2005 Int Workshop on Performance Evaluation of Cracking and Surveillance.2005:217-219.

［12]JIN Lisheng，TIAN Lei，WANG Rongben，et al.An improved OSCU method for image segmentation［C]//IEEE ICSP 2006 Proc，2006:159-168.