船舶溢油應急處置群體選擇偏好

王立坤

(上海海事大學交通運輸學院，上海 200135)

0 引言

2006—2008年，我國沿海共發生船舶溢油污染事故367起，總溢油量達2 221 t，對海洋生態環境和資源造成嚴重威脅.［1]為此，對船舶溢油事故的應急處置應予以高度重視，以減少溢油事故造成的環境污染與財產損失.

船舶溢油應急處置的成功很大程度上取決于行動方案的正確選擇與執行.危機下的情況復雜，個體的認知、經驗也很有限，個體很可能作出錯誤的決策或不執行正確方案，而海事溢油應急處置的決策往往由群體集成眾多個體的選擇偏好，因此，在確知個體對方案選擇概率的基礎上，有必要針對群體如何集成個體對方案的選擇偏好進行研究.

目前，有關群體決策的研究主要集中在基礎理論與技術方法層面.YU［2]在給定的決策空間上定義群體效用函數集，并以烏托邦為例研究群體決策的屬性，給出使群體決策缺陷最小的解決方案.SAH等［3]指出經濟系統中個人判斷存在誤差，群體決策會減少個體判斷的誤差，其效果主要受組織架構的影響.

盡管群體決策的理論相對比較成熟，但對溢油應急處置方面的研究仍集中于個體層面.如張欣［4]曾定性分析船舶溢油應急處置中個體決策的失誤，并用CREAM模型測算人誤致因與人誤二者間的相關性.

為此，本文首先對船舶溢油應急處置所涉及的群體選擇組成要素進行形式化描述，在此基礎上，以事故報告、溢油先期處理、現場查看、應急計劃啟動和清污方法制定等決策事件為對象，運用群體決策理論對船舶溢油應急處置的選擇偏好進行分析，并就如何提高群體決策水平提出相應的措施.

1 船舶溢油應急處置群體選擇的形式化描述

船舶溢油應急處置群體選擇由事件D，群體構成N，方案e和決策規則f等4個要素組成.

(1)事件D.船舶溢油應急處置所涉及的決策事件用D={D1，D2，D3，D4，D5}描述，其中Di(i=1，2，3，4，5)表示第 i個事件.

(2)群體構成N.船舶溢油應急處置涉及15個個體，N={n1，n2，…，nj，…，n15}，這些個體又分別構成6 個群體{N1，N2，…，Nq，…，N6}，其中 nj(j=1，2，…，15)表示第 j個個體，Nq(q=1，2，… ，6)表示第q個群體.

(3)決策方案e.對于決策事件D1和D3，存在唯一正確方案，記為e11和e31;對于其他決策事件Di，存在若干方案，eim記為與Di相關的第m個方案.

(4)決策規則f.可分為同質委員會、非同質委員會和層級模型等3類.同質委員會和非同質委員會規則以“投票達到k票通過方案(k為方案通過票數)”的方式作出決策，層級規則以“最高層確定方案”方式作出決策.［5-6]

根據2000年《中國海上船舶溢油應急計劃》［7]，船舶溢油應急處置中涉及的決策事件和對應方案見表1.

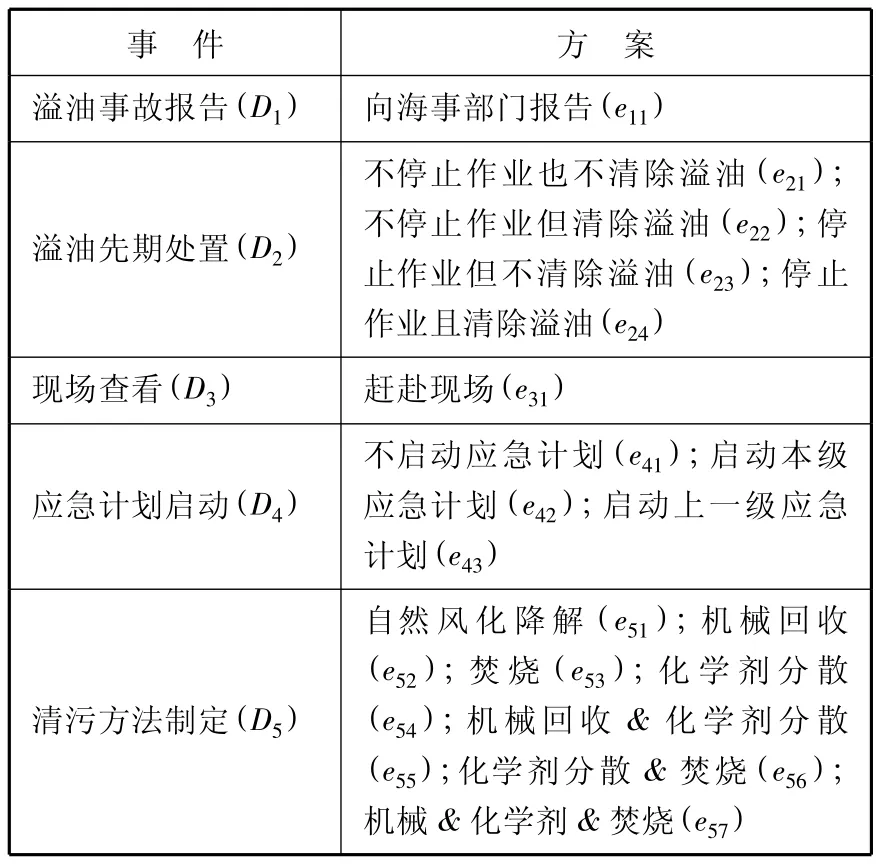
表1 事件和對應方案

應急處置群體由下列決策人構成:船長(n1)，輪機長(n2)，大副(n3)，船公司代理(n4)，應急值班人員(n5)，指揮中心人員(n6)，轄區應急總指揮(n7)，轄區應急副總指揮(n8)，局級應急總指揮(n9)，局級應急副總指揮(n10)，現場總指揮(n11)，現場副總指揮(n12)，專家(設為 n13，n14，n15).

2 群體選擇偏好分析

2.1 假定

對有唯一正確方案的事件Di(i=1，3):若個體nj執行正確方案，記為g(nj)=ei1，nj執行正確方案ei1的概率記為P(g(nj)=ei1);群體Nq對個體執行方案的概率集成記為P(f(Nq)=ei1)，在k票規則下的概率記為P(k)(f(Nq)=ei1).

對其他有若干決策方案的事件Di(i=2，4，5):若個體nj選擇某方案，則記為g(nj)=eim，nj選擇eim的概率記為P(g(nj)=eim);群體Nq對個體選擇某方案的概率集成記為P(f(Nq)=eim)，在k票規則下的概率記為P(k)(f(Nq)=eim).

2.2 事故報告選擇偏好

按規定，發生溢油后必須進行事故報告，即采用同質或非同質委員會模型進行選擇時，k=0;但若k=0，則無法明確決策主體.因此，必須針對k>0時的選擇偏好情況展開分析.

2.2.1 基于同質委員會的分析

(1)基本公式.設群體為 N1={n1，n2，n3，n4}，決策事件為事故報告(D1)，采用同質委員會和k票規則.令P(g(nj)=e11)=p1，則群體N1選擇e11的概率為

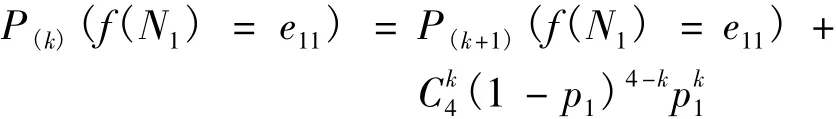
當k=1～4時，N1同質群體選擇偏好見表2.

表2 N1同質群體選擇偏好

(2)分析.令 p1在［0，1]內變化，可得 k值不同時的事故報告概率，見圖1.由圖1可知:隨著k值的減少，執行事故報告方案的概率增加;隨著決策個體nj執行事故報告方案的概率p1增大，群體N1報告事故的概率增加;當采用1票規則，或2票規則且p1>0.24，或3票規則且p1>0.78時，群體進行事故報告的概率會高出船長獨自決策的概率.因此，為及時、準確地報告事故，在實踐中可設置k=1票規則，即船長、輪機長、大副和代理中的任一人有權最終作出事故報告.此外，若能提升船長等報告事故的偏好，也能使事故的報告更及時、準確.

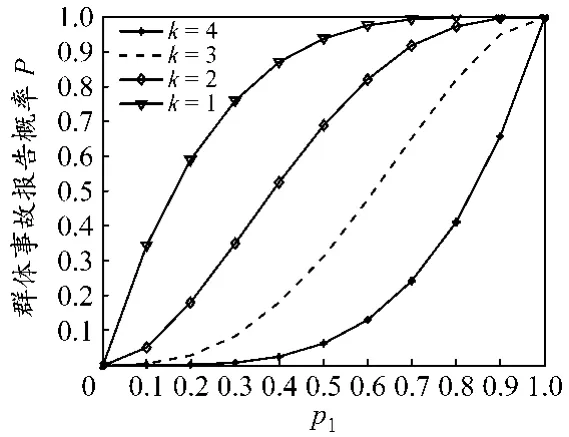
圖1 p1變化的事故報告概率

2.2.2 基于非同質委員會的分析

(1)基本公式.由于船長是首要決策者，事故報告決策事件D1也可采用非同質委員會模型.為不失一般性，設{n2，n3，n4}擁有 1 票，n1擁有的票數分別為 1～5票，k=3.令 P(g(n1)=e11)=p2，P(g(nj)=e11)=p3(j=2，3，4)，則群體執行事故報告方案的概率P(f(N1)=e11)見表3.

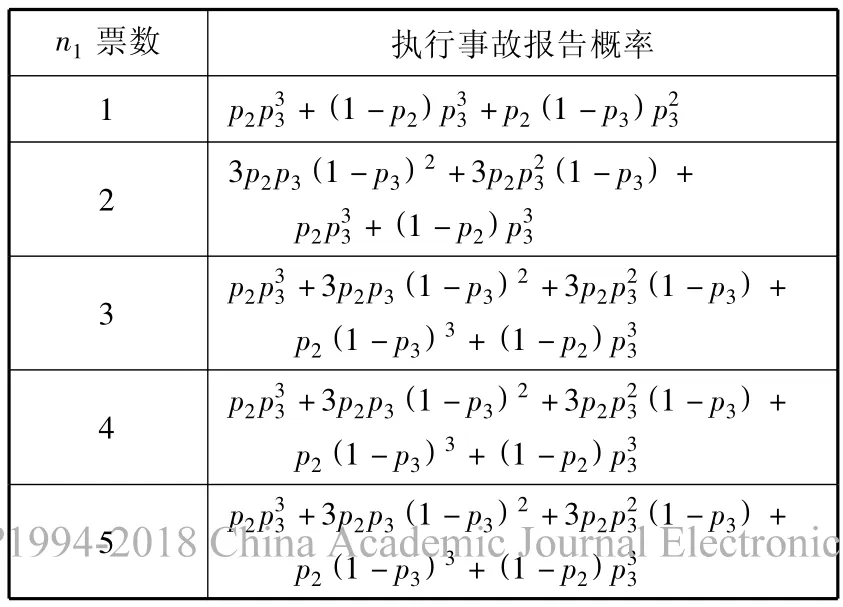
表3 N1非同質群體選擇偏好

(2)個體權重與方案執行關系分析.個體權重可用個體分配的票數表示.設船長分配票數分別為1～5票，其他個體均為1票，則對應p2=0.4(p3=0.6)，p2=0.5(p3=0.5)，p2=0.6(p3=0.4)和 p2=0.7(p3=0.3)等4種情況下，得到N1執行方案e11的概率，見圖2.

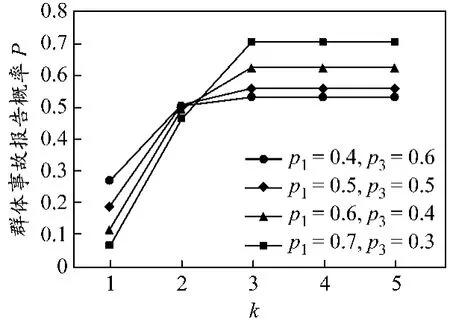
圖2 k變化的事故報告概率

由圖2可知，當k≥3時，執行事故報告方案的概率不隨票數的增加而變化，說明當船長的權重高于某個數值時，決策結果不受他人影響.

(3)個體概率與方案執行關系分析.分別令p2=0.2，0.4，0.6，0.8 和 1，當 k=4，p3∈(0，1)時，執行事故報告方案f(N1)=e11的概率見圖3.

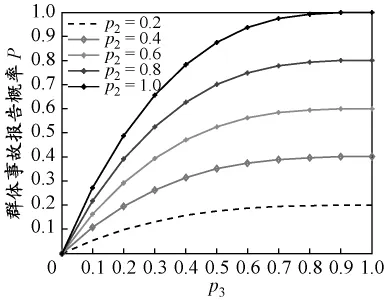
圖3 p3變化的事故報告概率

分別令 p3=0.2，0.4，0.6，0.8 和 1，當 k=4，p2∈(0，1)時，執行事故報告方案f(N1)=e11的概率偏好見圖4.

圖4 p2變化的事故報告概率

由圖3和4可知，隨著個體事故報告偏好的提高，群體執行事故報告的概率也提高，其中船長的影響高于其他人.

2.3 溢油先期處置選擇偏好

(1)一般公式.設群體為N2={n1，n2，n3}，決策事件為船舶溢油先期處置D2，決策規則采用層級模型.［8]首先，大副和輪機長提出處置方案提交給船長，設 V(n1)=1，V(n2)=0，V(n3)=0，V(n1，n2)=1，V(n1，n3)=1，V(n2，n3)=1，V(n1，n2，n3)=1，其中V(nj)=1和V(nj)=0分別表示當nj選擇某方案時，此方案被通過和未被通過.根據慣例，有P(g(n1)=e2m|g(n2)=e2m，P(g(n3)=e2m)=1;另采用 SHARPLEY［9]指數計算，得 P(g(n1)=e2m|g(n2)=e2m)和 P(g(n1)=e2m|g(n3)=e2m)均為1/3.令不同決策人選擇溢油事故先期處理方案e2m的概率為大副P(g(n2)=e2m)=p4，輪機長P(g(n3)=e2m)=p5，船長 P(g(n1)=e2m)=p6，得群體選擇先期處置方案e2m的概率

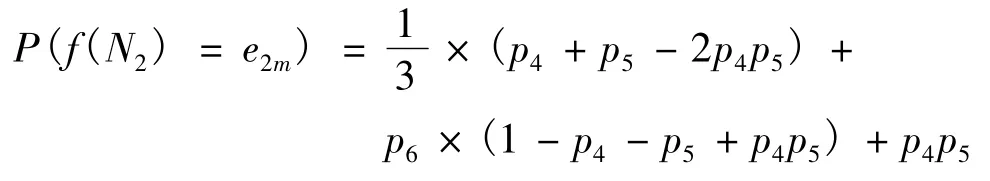
(2)分析.設 p4=p5，且分別取 0.2，0.4，0.6，0.8和1，當p6∈(0，1)時，選擇某先期處置方案 e2m的概率見圖5.

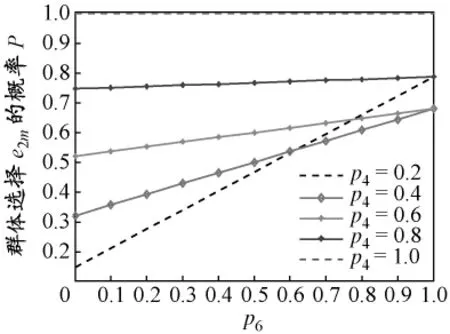
圖5 p6變化方案的通過概率

設 p6分別取 0.2，0.4，0.6，0.8 和 1，p4=p5，當p4∈(0，1)時，選擇先期處置方案e2m的概率見圖6.

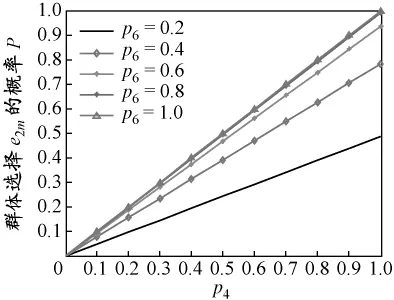
圖6 p4變化方案的通過概率

由圖5可知，若輪機長和大副均選擇某種先期溢油處置方案時，該方案通過;若輪機長和大副選擇某方案的概率較低時，該方案最終通過的概率主要受船長偏好的影響.由圖6可知，若船長傾向于選擇某方案，而輪機長和大副拒絕此方案，則方案通過的概率較高，但低于船長的個體偏好;若輪機長和大副都傾向于選擇某方案，則該方案的最終通過將不受船長個體偏好的影響.

3 模型擴展

以上對事故報告和先期處理2類事件的群體決策進行建模和分析，基于同樣原理，可給出船舶溢油應急的其他3個主要決策事件的方案選擇偏好，見表4.

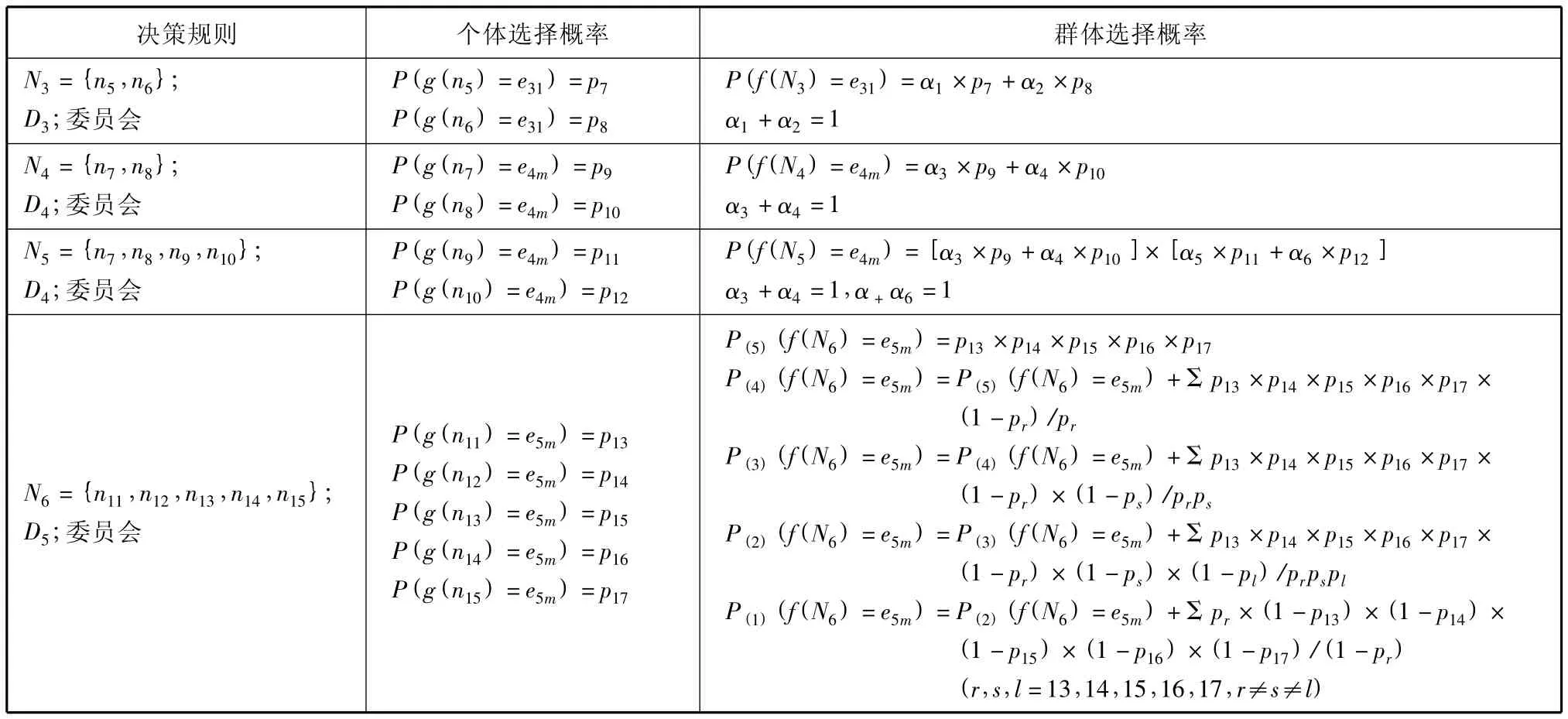
表4 群體選擇偏好

4 結束語

本文利用同質委員會、非同質委員會和層級模型等決策規則，給出船舶溢油應急處置中主要決策事件的群體選擇偏好，研究表明:

(1)根據應急預案，對于溢油事故報告事件，必須選擇向海事部門報告的方案;對于現場查看事件，必須選擇趕赴現場的方案.因此，對于類似具有明確規定的決策可采用委員會模型和1票規則，從而保證該方案的準確和及時實施.

(2)對于需根據具體情境而采取特定方案的決策事件，可采用層級模型，并賦予最終決策者較大的權重因子.一方面可減少個體決策的誤差，另一方面既可在決策者偏好不一致時平衡各方的偏好，也可在決策者偏好一致時疊加決策者的偏好.

［1]中華人民共和國環境保護部.中國環境狀況公報［EB/OL].(2009-12-20)［2009-12-25].http://www.zhb.gov.cn/plan/zkgb.

［2]YU P L.A class of solutions for group decision problems［J].Manage Sci，1973，19(8):936-946.

［3]SAH R K，STIGLITZ J E.The architecture of economic systems:hierarchies and polyarchies［J].Am Economic Rev，1986，76(4):716-727.

［4]張欣.人的失誤模型在船舶溢油事故應急中的應用分析［J].中國航海，2008，31(4):360-363.

［5]李武，席酉民，成思危.群體決策過程組織研究述評［J].管理科學學報，2002，5(2):55-66.

［6]李武，席酉民.二分群體決策規則約束條件研究［J].管理工程學報，2002，16(4):38-41.

［7]中華人民共和國海事局.中國海上船舶溢油應急計劃［R].北京:中華人民共和國海事局，2000.

［8]BRINK R V D，STEFFEN F.Decision making power in Hierarchies［C/OL]//Annu Meeting of the American Political Sci Assoc.Pennsylvania:2006.(2006-03-16)［2009-09-30].http://congress.utu.fi/epcs2006/docs/F7_steffen.pdf.

［9]SHARPLEY L S.A value for n-person games［M].Princeton:Princeton University Press，1953:307-317.