構(gòu)建與解讀“星體”模型

俞麗萍

(浙江上虞春暉中學(xué),浙江上虞 312353)

1 構(gòu)建

作用特征:兩個(gè)物體在相互間力的作用下,繞著某一點(diǎn)做勻速圓周運(yùn)動(dòng).

遵循規(guī)律:①兩個(gè)物體做勻速圓周運(yùn)動(dòng)的角速度ω相同、周期 T相同.

②兩個(gè)物體做勻速圓周運(yùn)動(dòng)的半徑與物體的質(zhì)量成反比,若物體的質(zhì)量分別為 m1、m2,物體的運(yùn)動(dòng)半徑分別為r1、r2,則 Fn=m1ω2r1=m2ω2r2,所以得到 m1r1=m2r2.

2 解讀

2.1 從“雙人”到“雙星”

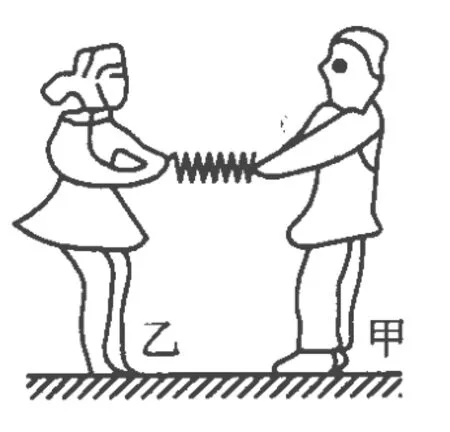
圖1

例1.甲、乙兩名溜冰運(yùn)動(dòng)員,面對(duì)面拉著彈簧秤做圓周運(yùn)動(dòng)的溜冰表演,如圖 1所示.已知 M甲=80 kg,M乙=40 kg,兩人相距0.9 m,彈簧秤的示數(shù)為96 N,下列判斷正確的是

(A)兩人的線速相同,約為40 m/s.

(B)兩人的角速相同,約為2 rad/s.

(C)兩人運(yùn)動(dòng)半徑相同,都為0.45 m.

(D)兩人運(yùn)動(dòng)半徑不同,甲為0.3 m,乙為0.6 m.

解析:甲、乙兩運(yùn)動(dòng)員在相互間拉力的作用下做勻速圓周運(yùn)動(dòng),拉力提供向心力,由 M甲r甲=M乙r乙,r甲+r乙=0.9 m,可求得 r甲=0.3 m,r乙=0.6 m.Fn=M甲ω2r甲=M乙ω2r乙,解得 ω=2 rad/s,故此題選(B)、(D).

例2.(2008年寧夏卷)天文學(xué)家將相距較近、僅在彼此的引力作用下運(yùn)行的兩顆恒星稱為雙星.雙星系統(tǒng)在銀河系中很普遍.利用雙星系統(tǒng)中兩顆恒星的運(yùn)動(dòng)特征可推算出它們的總質(zhì)量.已知某雙星系統(tǒng)中兩顆恒星圍繞它們連線上的某一固定點(diǎn)分別做勻速圓周運(yùn)動(dòng),周期均為 T,兩顆恒星之間的距離為 r,試推算這個(gè)雙星系統(tǒng)的總質(zhì)量.(引力常量為G)

解析:設(shè)兩顆恒星的質(zhì)量分別為 m1、m2,做圓周運(yùn)動(dòng)的半徑分別為 r1、r2,角速度分別為 ω1,ω2.根據(jù)題意有

根據(jù)萬有引力定律和牛頓定律,有

聯(lián)立以上各式解得

根據(jù)角速度與周期的關(guān)系知

聯(lián)立(3)、(5)、(6)式解得

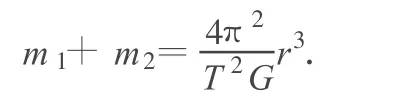
點(diǎn)評(píng):在“雙人”模型中,若將兩運(yùn)動(dòng)員看成是兩顆恒星,將兩運(yùn)動(dòng)員之間的拉力看成是萬有引力,那么,對(duì)于“雙星”模型的理解也就不難了.

2.2 從“雙星”到“雙電荷”

圖2

例3.如圖2所示,兩個(gè)正、負(fù)點(diǎn)電荷,在庫侖力作用下,它們以兩者連線上的某點(diǎn)為圓心,做勻速圓周運(yùn)動(dòng),以下說法正確的是

(A)它們所需的向心力大小不相等.

(B)它們做勻速圓周運(yùn)動(dòng)的角速度相等.

(C)它們的線速度與其質(zhì)量成反比.

(D)它們運(yùn)動(dòng)半徑與電量成反比.

解析:兩個(gè)正、負(fù)點(diǎn)電荷,以兩者連線上的某點(diǎn)為圓心做勻速圓周運(yùn)動(dòng),庫侖力提供向心力,兩個(gè)點(diǎn)電荷構(gòu)成雙星模型,故兩者向心力的大小相等,角速度相等,又由于m1r1=m2r2,所以 m1ω r1=m2ω r2,m1v1=m2v2, 故此題選(B)、(C).

2.3 從“雙星”到“三星”

例4.(2006年廣東卷)宇宙中存在一些離其他恒星較遠(yuǎn)的、由質(zhì)量相等的三顆星組成的三星系統(tǒng),通常可忽略其他星體對(duì)它們的引力作用.已觀測(cè)到穩(wěn)定的三星系統(tǒng)存在兩種基本的構(gòu)成形式:一種是三顆星位于同一直線上,兩顆星圍繞中央星在同一半徑為 R的圓軌道上運(yùn)行;另一種形式是三顆星位于等邊三角形的三個(gè)頂點(diǎn)上,并沿外接于等邊三角形的圓形軌道運(yùn)行.設(shè)每個(gè)星體的質(zhì)量均為 m.

(1)試求第1種形式下,星體運(yùn)動(dòng)的線速度和周期.

(2)假設(shè)兩種形式星體的運(yùn)動(dòng)周期相同,第2種形式下星體之間的距離應(yīng)為多少?

解析:第1種形式下,由萬有引力定律和牛頓第二定律,得

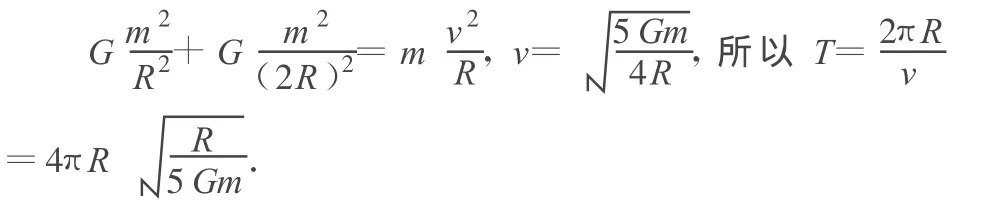
第2種形式下,由萬有引力定律和牛頓第二定律,得

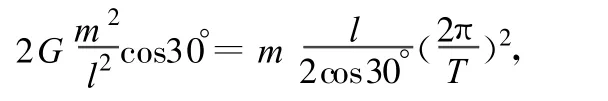
2.4 從“三星”到“四星”

例5.宇宙中存在一些離其他恒星很遠(yuǎn)的四顆星組成的四星系統(tǒng),通常可忽略其他星體對(duì)它們的引力作用,穩(wěn)定的四星系統(tǒng)存在兩種基本的構(gòu)成形式:一種形式是四顆質(zhì)量相等的星位于正方形的四個(gè)頂點(diǎn)上,沿外接于正方形的圓形軌道運(yùn)行:另一種形式是四顆質(zhì)量不等的星位于同一直線上,間距相等,均圍繞中點(diǎn)做圓周運(yùn)動(dòng),已知第一種形式中每顆星質(zhì)量均為m,正方形邊長(zhǎng)為a,求它們的運(yùn)行周期T.

解析:已知第一種形式中每顆星質(zhì)量均為m,正方形邊長(zhǎng)為a,每顆星體在其他三個(gè)星體的萬有引力作用下圍繞正方形對(duì)角線的交點(diǎn)做勻速圓周運(yùn)動(dòng),由萬有引力定律和向心力公式得

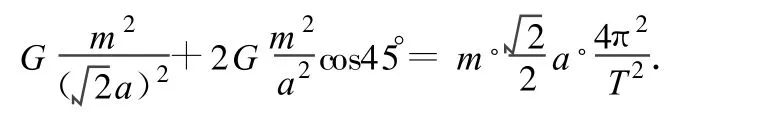
解得周期

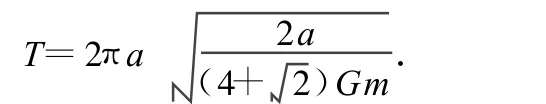
點(diǎn)評(píng):從數(shù)量而言,雙星、三星、四星星體數(shù)量逐漸增加,而且“三星”與“四星”都出現(xiàn)了兩種不同的穩(wěn)定形式,但無論是哪一種形式,對(duì)研究對(duì)象進(jìn)行受力情況分析,找出向心力的來源是解決問題的關(guān)鍵所在.

2.5 從“雙星”到“暗星”

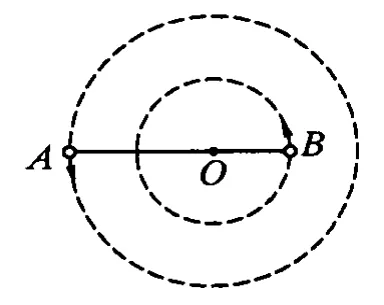
圖3

例6.(2006年天津卷)神奇的黑洞是近代引力理論所預(yù)言的一種特殊天體,探尋黑洞的方案之一是觀測(cè)雙星系統(tǒng)的運(yùn)動(dòng)規(guī)律.天文學(xué)家觀測(cè)河外星系大麥哲倫云時(shí),發(fā)現(xiàn)了LMCX-3雙星系統(tǒng),它由可見星A和不可見的暗星B構(gòu)成.兩星視為質(zhì)點(diǎn),不考慮其他天體的影響,A、B圍繞兩者連線上的O點(diǎn)做勻速圓周運(yùn)動(dòng),它們之間的距離保持不變,如圖3所示.引力常量為 G,由觀測(cè)能夠得到可見星 A的速率v和運(yùn)行周期T.

(1)可見星 A所受暗星B的引力FA可等效為位于O點(diǎn)處質(zhì)量為m′的星體(視為質(zhì)點(diǎn))對(duì)它的引力,設(shè) A和B的質(zhì)量分別為m1、m2,試求 m′(用 m1、m2表示);

(2)求暗星 B的質(zhì)量m2與可見星 A的速率v、運(yùn)行周期T和質(zhì)量m1之間的關(guān)系式;

(3)恒星演化到末期,如果其質(zhì)量大于太陽質(zhì)量 ms的2倍,它將有可能成為黑洞.若可見星 A的速率v=2.7×105m/s,運(yùn)行周期 T=4.7π×104s,質(zhì)量 m1=6ms,試通過估算來判斷暗星B有可能是黑洞嗎?

解析:(1)設(shè) A、B的圓軌道半徑分別為r1、r2,由題意知,A、B做勻速圓周運(yùn)動(dòng)的角速度相同,設(shè)其為ω.由牛頓運(yùn)動(dòng)定律,有

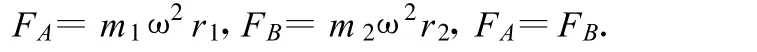
設(shè) A、B之間的距離為r,又 r=r1+r2,由上述各式得

由萬有引力定律可得

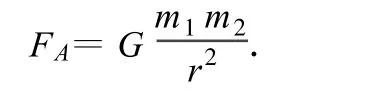
將(1)式代入得

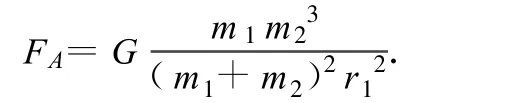
(2)由牛頓第二定律,有

又因?yàn)榭梢娦?A的軌道半徑

由(2)～(4)式解得

(3)將 m1=6ms代入(5)式,得

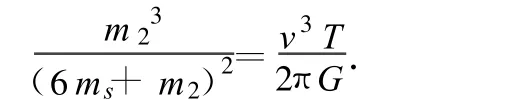
代入數(shù)據(jù)得

m2=nms(n＞0),將其代入(6)式得

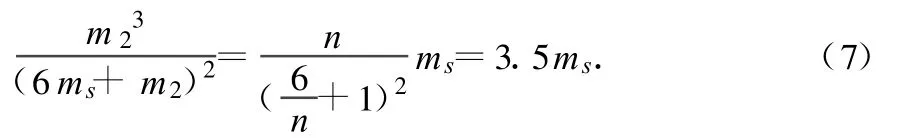
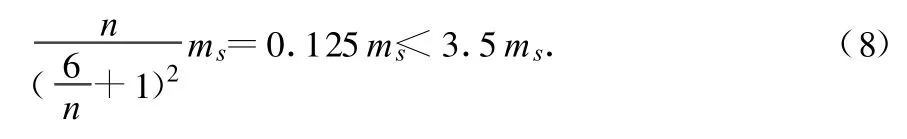
若使(7)式成立,則 n必大于2,即暗星B的質(zhì)量 m2必大于2ms,由此得出結(jié)論:暗星B有可能是黑洞.

點(diǎn)評(píng):利用雙星系統(tǒng)的運(yùn)動(dòng)規(guī)律可以來研究不可見的暗星B的等效質(zhì)量m′,進(jìn)而探討暗星B是否有可能是黑洞.

無論是雙星還是多星,處理“星體”模型的關(guān)鍵是通過對(duì)研究對(duì)象的受力分析明確向心力的來源,通過幾何關(guān)系確定圓周運(yùn)動(dòng)的半徑,再利用圓周運(yùn)動(dòng)的運(yùn)動(dòng)規(guī)律展開討論.