EMD與二階循環(huán)平穩(wěn)分析在電動(dòng)機(jī)軸承故障診斷中的應(yīng)用

王小卉，楊潔明

（1.湛江師范學(xué)院 機(jī)電工程系，廣東 湛江 524048；2.太原理工大學(xué) 機(jī)電研究所，太原 030024）

在各種機(jī)械故障中，由于軸承而發(fā)生故障的概率很高。軸承故障早期一般表現(xiàn)為內(nèi)圈、外圈或滾動(dòng)體的局部點(diǎn)蝕，隨著軸承的運(yùn)轉(zhuǎn)，由于滾動(dòng)體與內(nèi)、外圈沖擊而產(chǎn)生振動(dòng)，這時(shí)的振動(dòng)頻率為軸承各部分的固有頻率［1］，與此同時(shí)還有一個(gè)軸承旋轉(zhuǎn)周期，此周期大于沖擊產(chǎn)生的周期，對(duì)沖擊產(chǎn)生調(diào)制作用，形成了調(diào)制信號(hào)［2］。軸承這種振動(dòng)信號(hào)的二階統(tǒng)計(jì)特征具有周期時(shí)變的特點(diǎn)，于是近年來(lái)人們開(kāi)始轉(zhuǎn)向研究循環(huán)平穩(wěn)分析方法以實(shí)現(xiàn)軸承等旋轉(zhuǎn)機(jī)械的故障診斷［3-4］。

實(shí)際上，故障信號(hào)不一定能直接從故障零件中取得，間接取得的信號(hào)又往往被強(qiáng)噪聲覆蓋，已有研究開(kāi)始試用預(yù)處理和循環(huán)分析結(jié)合的方法處理信號(hào)［5］。考慮到電動(dòng)機(jī)軸承振動(dòng)信號(hào)的特性，用非平穩(wěn)信號(hào)的EMD方法［6-7］，在分解重構(gòu)信號(hào)后進(jìn)行循環(huán)自相關(guān)，并應(yīng)用譜相關(guān)切片集合分析法排除交叉干擾，以期達(dá)到快速準(zhǔn)確提取故障特征的目的。

1 二階循環(huán)平穩(wěn)解調(diào)性能分析

如果信號(hào)x（t）滿足條件：從一階到二階時(shí)變統(tǒng)計(jì)量都存在，且都是時(shí)間的周期函數(shù)，則該信號(hào)為二階循環(huán)平穩(wěn)信號(hào)。其表達(dá)式為：

式中：fz為載波頻率，Hz；θ為相位角，rad；Ai為調(diào)節(jié)因子；ft為調(diào)制頻率，Hz。

統(tǒng)計(jì)學(xué)中，信號(hào)x（t）的循環(huán)自相關(guān)函數(shù)表達(dá)式為：

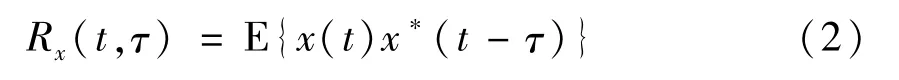
式中：τ為時(shí)間滯后量；x*（t）為x（t）的共軛。假定信號(hào)滿足時(shí)間遍歷性，離散化后，該式可表達(dá)為：

由此可見(jiàn)Rx（t，τ）是關(guān)于時(shí)間t（固定τ）的周期為T(mén)0的函數(shù)。所以，可對(duì)（時(shí)變）相關(guān)函數(shù)Rx（t，τ）做Fourier展開(kāi)，并且取a＝m／T0（循環(huán)頻率），其中m為整數(shù)（m＝1，2，3，…），得到：

由上式可推知：循環(huán)自相關(guān)函數(shù)的非零值只存在于循環(huán)頻率等于調(diào)制頻率及其2倍頻、2倍載波頻率、2倍載波頻率與調(diào)制頻率及其2倍頻的和差等地方，而在其他地方均為零［6］。

以（1）式所表達(dá)的信號(hào)為例，為方便分析，取n＝1（即i＝1），取Ai＝1.5，ft＝15，fz＝100，θ＝30，設(shè)信號(hào)：x1＝x（t），x2＝x（t）+0.8n（t），x3＝x（t）+0.8wgn，x4＝x（t）+1.5n（t）+1.5wgn。

其中n（t）為噪聲服從正態(tài)分布的隨機(jī)平穩(wěn)遍歷白噪聲，wgn為Gauss噪聲。

用循環(huán)自相關(guān)三維圖分析可實(shí)現(xiàn)調(diào)制信號(hào)的解調(diào)，且可利用循環(huán)頻率域高、低頻率段內(nèi)得到的信息進(jìn)行相互驗(yàn)證，排除干擾。但三維圖運(yùn)算量大，信息冗余。二維的循環(huán)自相關(guān)切片分析得到的信息與三維圖一致，如圖1所示。在信號(hào)x1到x4，τ＝0時(shí)的循環(huán)自相關(guān)切片圖中可以發(fā)現(xiàn)，循環(huán)頻率信息分布在循環(huán)頻率域高、低兩個(gè)不同的頻段。

圖1 信號(hào)x1，x2，x3，x4的循環(huán)自相關(guān)單切片（τ＝0）

在低頻段僅含調(diào)制頻率信息15 Hz，30 Hz（ft，2ft）；高頻段既有調(diào)制頻率也有載波頻率的信息，200 Hz，（200±15）Hz，（200±30）Hz，（2fz，2fz±ft，2fz±2ft）。圖1b與圖1c分別是帶有普通噪聲x2和Gauss噪聲信號(hào)x3的循環(huán)相關(guān)分析切片，說(shuō)明循環(huán)平穩(wěn)分析對(duì)普通與Guass噪聲均有免疫性。但強(qiáng)噪聲下單獨(dú)使用循環(huán)平穩(wěn)分析就難以排除干擾了，圖1d是含Gauss強(qiáng)噪聲信號(hào)x4的循環(huán)相關(guān)切片圖，循環(huán)頻率被完全覆蓋。上述說(shuō)明，二維循環(huán)平穩(wěn)分析雖然有噪聲免疫功能，但在強(qiáng)噪聲下仍難以提取循環(huán)特征頻率，抗干擾能力差。

2 強(qiáng)噪聲信號(hào)的EMD預(yù)處理

實(shí)際采集到的信號(hào)會(huì)帶有很強(qiáng)的噪聲干擾，此時(shí)單用平穩(wěn)分析很難達(dá)到預(yù)期診斷效果（圖1d），這就需要選擇一種適用于非平穩(wěn)信號(hào)的消噪方法。

經(jīng)驗(yàn)?zāi)B(tài)分解算法（EMD）基于信號(hào)的局部特征時(shí)間尺度，可把信號(hào)分解為若干個(gè)基本模式分量（IMF）之和，分解出的各個(gè)IMF分量突出了數(shù)據(jù)的局部特征，是一種自適應(yīng)的信號(hào)分解方法，具有很高的信噪比，適用于非平穩(wěn)、非線性過(guò)程，可采用EMD方法對(duì)振動(dòng)信號(hào)進(jìn)行預(yù)處理。設(shè)計(jì)的基于EMD的消噪步驟如下：

（1）提取本征函數(shù)IMF（ci）。分解信號(hào)x4，得出前6項(xiàng)IMF。

（2）對(duì)每項(xiàng)IMF分別作FFT變換，根據(jù)圖2顯示各模態(tài)分量的頻率分布，可判別c2～c5的頻率范圍為10～250 Hz，包含了信號(hào)x4的所有特征頻率（200 Hz，200 Hz±15 Hz，30 Hz等）。

圖2 原信號(hào)及本征函數(shù)c1～c5 FFT圖

（3）選用c2～c5進(jìn)行信號(hào)重構(gòu)，即使x4＝c2+c3+c4+c5（相當(dāng)于帶通濾波）。做重構(gòu)信號(hào)τ＝0處的循環(huán)自相關(guān)切片得到圖3，原來(lái)被噪聲湮滅的載波頻率（200 Hz）和調(diào)制頻率（15 Hz）都能反映出來(lái)，與圖1d比較，證實(shí)了EMD分解重構(gòu)的消噪效果。

圖3 重構(gòu)信號(hào)的循環(huán)自相關(guān)切片

3 軸承故障試驗(yàn)分析

3.1 故障說(shuō)明

試驗(yàn)采用Y160M2-8型電動(dòng)機(jī)軸承故障試驗(yàn)臺(tái)：主要設(shè)備有壓電式加速度傳感器、KISTLER5134型耦合器、DEWEtron十六通道信號(hào)采集器、磁粉制動(dòng)器、齒輪箱、加載機(jī)構(gòu)和電源。試驗(yàn)對(duì)象為6309型軸承。

試驗(yàn)數(shù)據(jù)如下：鋼球直徑Dw＝17.5 mm，球組節(jié)圓直徑Dpw＝72.5 mm，鋼球數(shù)Z＝8，接觸角α＝0，試驗(yàn)時(shí)外圈固定不動(dòng)，用渦流位移傳感器測(cè)得主軸轉(zhuǎn)速為715 r／min，轉(zhuǎn)頻fr＝11.9 Hz。計(jì)算［5］可得：內(nèi)圈通過(guò)頻率fi＝59 Hz，外圈通過(guò)頻率fe＝36 Hz，鋼球通過(guò)頻率fb＝23.2 Hz，保持架旋轉(zhuǎn)頻率fc＝4.5 Hz。

如果某部位出現(xiàn)點(diǎn)蝕，循環(huán)統(tǒng)計(jì)量在相應(yīng)的頻率處出現(xiàn)能量峰值，據(jù)此可判別故障部位。

3.2 故障的分析及診斷

采集數(shù)據(jù)前，將多套6309型軸承進(jìn)行輕度人為破壞，分別構(gòu)成輕微的鋼球故障、內(nèi)圈故障、外圈故障及混合故障，以模擬工況下的各種早期故障。此處分析內(nèi)圈故障軸承運(yùn)轉(zhuǎn)時(shí)從電動(dòng)機(jī)端蓋間接采集的信號(hào)。

電動(dòng)機(jī)軸承的運(yùn)行特點(diǎn)決定了其振動(dòng)信號(hào)具有一定的二階循環(huán)平穩(wěn)性。故可以利用循環(huán)平穩(wěn)分析來(lái)提取故障信息。

由第1節(jié)分析的結(jié)論可以得出在τ＝0時(shí)的譜相關(guān)切片的低頻處有ft，2ft甚至3ft出現(xiàn)峰值。在整個(gè)軸承系統(tǒng)中，軸承如果出現(xiàn)故障，其產(chǎn)生的故障頻率可作為載波頻率，被轉(zhuǎn)頻調(diào)制；同時(shí)又作為調(diào)制頻率，去調(diào)制系統(tǒng)頻率（系統(tǒng)頻率大概為1 560 Hz）。這里所提的切片集合分析的前提就是依據(jù)第2種情況，即將各種故障特征頻率視為調(diào)制頻率，假如此特征頻率處的譜相關(guān)單切片圖上有相應(yīng)頻率出現(xiàn)峰值，那么此頻率則可以確定為故障頻率。這種方法的特點(diǎn)是針對(duì)性強(qiáng)，運(yùn)算量很小，在普通配置的計(jì)算機(jī)上便能實(shí)現(xiàn)。具體步驟為：

（1）消噪處理。試驗(yàn)信號(hào)只能間接由電動(dòng)機(jī)軸承端蓋采集，不是直接從故障軸承中采集，干擾很大。故先用EMD對(duì)內(nèi)圈故障信號(hào)進(jìn)行分解，選用本征函數(shù)c2～c5重構(gòu)。

（2）做重構(gòu)信號(hào)τ＝0處的循環(huán)自相關(guān)切片分析（圖4）。可以看出峰值出現(xiàn)在內(nèi)圈故障頻率58 Hz，45 Hz和71 Hz（約為內(nèi)圈故障頻率的1倍邊頻59 Hz±11.9 Hz）處，也能發(fā)現(xiàn)120 Hz（約為2倍內(nèi)圈故障頻率），但也有很多未知的干擾頻率，如29 Hz，48 Hz等亦出現(xiàn)峰值。

圖4 處理后信號(hào)循環(huán)自相關(guān)單切片圖

（3）對(duì)圖4中出現(xiàn)峰值的頻率處做循環(huán)譜密度切片集合分析，以排除干擾。如果是循環(huán)頻率，在SCD譜圖中會(huì)出現(xiàn)相應(yīng)信息，若不是則為干擾，可以排除。由圖5可見(jiàn)，在a＝29 Hz中沒(méi)有出現(xiàn)相應(yīng)的頻率，進(jìn)而被排除（同理48 Hz也被排除）。而在a＝59 Hz中則可明顯發(fā)現(xiàn)60 Hz的信息，再次驗(yàn)證此軸承發(fā)生了內(nèi)圈故障。

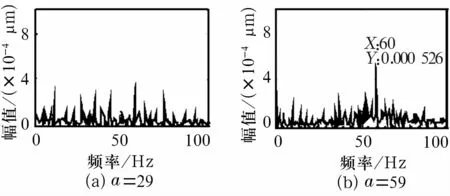
圖5 峰值頻率的循環(huán)譜切片集合分析

4 結(jié)束語(yǔ)

二階循環(huán)平穩(wěn)分析對(duì)噪聲有免疫性，可實(shí)現(xiàn)故障特征分量分離，但在現(xiàn)場(chǎng)采集信號(hào)時(shí)，間接采集的軸承早期故障信號(hào)容易湮沒(méi)在噪聲中，EMD算法對(duì)信號(hào)分解重構(gòu)進(jìn)行消噪，基本達(dá)到預(yù)期效果。

通過(guò)試驗(yàn)證明EMD消噪與二階SCA和SCD的綜合分析法結(jié)合能有效排除故障信號(hào)中的干擾頻率，提取微弱故障信息，此分析用到的僅是二維譜圖，相比運(yùn)算量龐大、信息冗余的三維譜圖，此法的運(yùn)算速度大大提高，能實(shí)現(xiàn)軸承早期故障的快速診斷，兼顧了效率與準(zhǔn)確率。