鐵路線路的歸一化放樣

姜晨光 路 奎 林長勝 蔡香玲 楊英姿 朱燁昕

(1.江南大學環境與土木工程學院,江蘇無錫 214122；2.山東省國土測繪院,山東濟南 250013；3.煙臺建設集團鋼結構有限公司,山東煙臺 264003；4.文登市建設局,山東文登 264400；5.山東宜華咨詢有限公司,山東威海 264200；6.無錫市建設局,江蘇無錫 214031)

1 概述

鐵路軌道幾何形位的科學性與準確性是確保鐵路列車行車安全的關鍵之一,要確保鐵路軌道幾何形位的準確性就必須依靠精細、高精度的測量技術。鐵路軌道幾何形位的基本要素包括軌距、水平、前后高低、軌向、軌底坡、曲線軌距加寬、曲線外軌超高、緩和曲線、限制坡度、豎曲線等。軌道的幾何形位應按靜態與動態兩種狀況進行管理。靜態幾何形位是軌道不行車時的狀態,采用道尺等工具進行測量。動態幾何形位是行車條件下的軌道狀態,采用軌道檢查車進行測量。曲線軌距加寬(高速鐵路一般不加寬)的方法是將曲線軌道內軌向曲線中心(圓心)方向移動,曲線外軌的位置則保持與軌道中心半個軌距的距離不變。曲線軌距的加寬值與機車車輛轉向架在曲線上的幾何位置有關。外軌超高度是指曲線外軌頂面與內軌頂面水平高度之差。鐵路緩和曲線及圓曲線的準確定位是鐵路軌道幾何形位確定中的關鍵工作,鐵路緩和曲線及圓曲線通常會給出曲線方程式,這些曲線方程式采用的都是數學坐標系坐標(比如圓曲線方程式以圓心為坐標原點、緩和曲線方程式以曲線起點為坐標原點),而鐵路測量與放樣時采用的是國家坐標系,故傳統的緩和曲線及圓曲線放樣方法是先確定曲線的起點、再按偏角法或切線支距法或弦線支距法或直角坐標法編制放樣數據表、然后再按與數據表對應的方法進行放樣。

傳統的緩和曲線及圓曲線放樣方法具有速度慢、效率低、精度不高、過程繁瑣等諸多弱點,可否實現緩和曲線及圓曲線的精準快速放樣,筆者及項目組在實踐的基礎上提出了鐵路線路歸一化放樣的思想,并在實際應用中取得了良好的效果,在此做一介紹。

2 鐵路緩和曲線及圓曲線的基本特征

緩和曲線是設置在直線和圓曲線之間或半徑相差較大的兩個轉向相同的圓曲線之間的一種曲率連續變化的曲線。緩和曲線的作用是曲率連續變化、便于車輛遵循,離心加速度逐漸變化滿足旅客舒適要求；超高橫坡度及加寬逐漸變化使行車更加平穩,與圓曲線協調配合增加了線形的美觀度。對緩和曲線的基本要求是可行性好、緩和性好、計算方便且公式簡單(便于在設計、施工中使用)。鐵路設置緩和曲線的目的是在曲線到直線、直線到曲線上,為使作用力不突變(平面上),平面曲線曲率 ρ應由∞→R；同時,使超高h在緩和曲線上逐步完成長度要求,其中L0為緩和曲線長度。緩和曲線的主要形式有三次拋物線、高次拋物線(4,5,7次拋物線)、三角函數線、雙紐線、回旋線、等。

2.1 回旋線

回旋線(見圖1)是曲率隨著曲線長度成比例變化的曲線,其基本公式為

式(1)中,r為任意點曲率半徑/m；l為起點到任一點的曲線長/m；A為長度量綱。r、l稱回旋線參數,它表示回旋線曲率變化的緩急程度。在緩和曲線終點處 l=L0、r=R,因此,有

回旋線的性質可概括為4點,即曲率按線形函數增大k=1/r=l/A2(A越大、曲率k越小、回旋線變化越慢；A越小、曲率k越大、回旋線變化越快)；所有回旋線都是幾何相似的；切線角 β與曲線長l的平方成正比；極角 δ近似為 β/3。

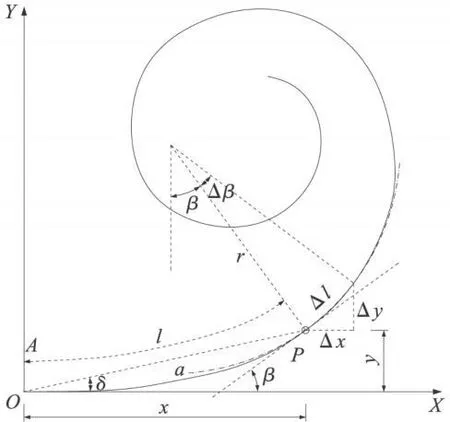
圖1 回旋線及其各相關要素

2.2 三次拋物線

三次拋物線的形式為

三次拋物線用作緩和曲線只能在 β≤24°的條件下使用。由于緩和曲線長度的確定主要考慮安全和舒適2個因素,因此,高速鐵路線路緩和曲線的設置條件是L0應足夠長,順坡兩端要圓順,要保證緩和曲線的曲率變化率為常量。現在,我國采用圓曲線來過渡,緩和曲線的曲率半徑變化率c為

式(4)中,L0為緩和曲線的長度,R為圓曲線半徑。

我國高速鐵路線路最小曲線半徑取50 m的整倍數,新建客運專線不同速度下的推薦圓曲線半徑見表1。客運專線線路的夾直線、圓曲線最小長度見表2(其中vmax為火車最大運行速度)。另外,鐵路通過設置豎曲線以限制向上的離心加速度,客運專線不同速度下的最小豎曲線半徑見表3,考慮運行安全性要求的豎曲線半徑見表4,應用時一般綜合表3和表4數值(即取2表中相應的大值)。

表1 客運專線不同速度下的圓曲線半徑

表2 客運專線線路夾直線、圓曲線最小長度

表3 客運專線不同速度下的最小豎曲線

表4 考慮運行安全性要求的豎曲線半徑

2.3 不同類型緩和曲線的特點

雙紐線(方程式為r=c/a)在極角為45°時曲率半徑最小,此后半徑增大至原點,全程轉角達到270°。回旋線、三次拋物線和雙紐線在極角較小(5°～6°)時幾乎沒有多少差別。隨著極角的增加,三次拋物線的長度比雙紐線的長度增加得快些,而雙紐線的長度又比回旋線的長度增加得快些。回旋線的曲率半徑減小得最快,而三次拋物線則減小最慢。從保證火車平順過渡的角度看,三種曲線都可以作為緩和曲線。目前我國鐵路采用三次拋物線。

3 鐵路線路的歸一化放樣方法

鐵路線路歸一化放樣方法實現的前提是將鐵路線路設計中所有的非國家坐標系統的線路坐標(比如鐵路圓曲線以圓心為坐標原點的坐標系統、緩和曲線以曲線起點為坐標原點的坐標系統等)轉換為國家坐標(高斯坐標)。假設某點的非國家坐標系統線路坐標為X′、Y′,該點在國家坐標系統中的對應坐標為 X、Y,則其坐標轉換模式為

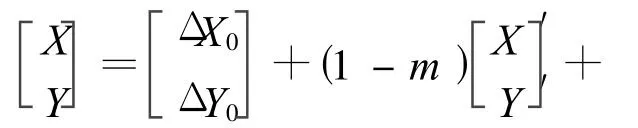
式(5)中,ΔX0、ΔY0、m 、θ,分別為 2 個平面坐標系間的平移、尺度、旋轉參數,總稱為平面轉換四參數。不難看出,要求出平面轉換四參數至少需要2個公共點。即先根據鐵路線路設計圖(CAD圖)獲得非國家坐標系統線路坐標中2個線路點的國家坐標(可在設計圖上直接獲得,也可利用Auto CAD的ID命令捕捉獲得,2個線路點一般應為曲線的起終點或應相距盡可能地遠)Xi、Yi,然后再根據2個線路點的線路設計坐標(即非國家坐標系統坐標或數學坐標)Xi′、Yi′借助式(5)即可求出平面轉換四參數,進而可將該非國家坐標系統線路坐標中各個線路點的設計坐標轉換為國家坐標,然后就可利用鐵路線路測量控制網中的控制點對所有的非國家坐標系統的線路設計點進行放樣(采用電子全站儀或 GPS)從而摒棄傳統的放樣方法。

由于鐵路線路一般很長,常跨越若干個高斯投影帶,因此,坐標換帶就成了必須重視的工作。另外,當線路點放樣精度要求較高且高斯投影變形又較大時,還應移動中央子午線位置以建立獨立的工程放樣控制網(比如特大橋控制網)。同時,采用GPS放樣時還存在GPS坐標與國家坐標的轉換問題及GPS高程與正常高的轉換問題。上述種種情況決定了鐵路線路歸一化放樣過程中必須熟悉大地坐標與高斯坐標間的相互轉換、GPS坐標與國家大地坐標間的相互轉換以及坐標換帶等基本理論并采用高精度的轉換方法。要實現上述高精度轉換,筆者建議采用以下公式。

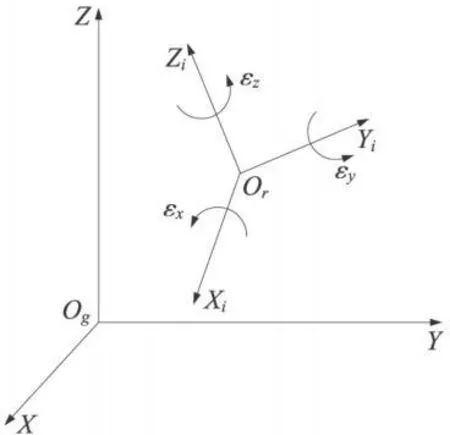
圖2 GPS坐標與國家大地坐標間的關系

3.1 GPS坐標與國家大地坐標的轉換

如圖2,GPS測量的坐標系是世界大地坐標系即WGS-84坐標系,而我國目前常見的三維坐標系為1954北京坐標系及1956黃海高程系,或1980國家大地坐標系及1985國家高程基準以及2000國家大地坐標系,故必須對GPS測量的三維定位成果必須進行換算,才能滿足鐵路測量的實際需要。GPS坐標與國家大地坐標間的轉換至少采用七參數轉換法,七參數轉換法需轉換區域內至少有3個已知國家坐標的控制點(3個已知控制點應均勻分布在轉換區域的邊緣附近),在這些國家控制點上獲取載波相位靜態觀測1～2 h的WGS-84系坐標(X,Y,Z)成果,再根據數學模型(見式(6))解算出七個轉換參數,然后即可對該轉換區域內所有的點進行2個不同坐標系間坐標的相互轉換。

式(6)中,Xi、Yi、Zi為國家坐標系的三維空間直角坐標；X、Y、Z為GPS的WGS-84系三維空間直角坐標；ΔX、ΔY、ΔZ為兩坐標原點間的平移參數(或叫原點距 )；K 為兩坐標系間的尺度比；εx、εy、εz為兩坐標系坐標軸間的旋轉角(旋轉參數)。

3.2 GPS高程與國家高程的轉換

GPS高程是基于WGS-84橢球的大地高高程(簡稱大地高),我國采用的高程系統則為正常高。GPS大地高是由地面點沿法線到WGS-84橢球體面的距離,正常高是地面點沿鉛垂線到似大地水準面的距離。將GPS測定的大地高轉為正常高的關鍵是求取大地高H與正常高h間的差值(即高程異常值 ξ)。其高程轉換的基本數學模型為

推算 ξ值的方法很多,常用的有GPS水準高程法和GPS重力高程法等。GPS水準高程方法又可分為平面擬合法、二次曲面擬合法、多面函數法、樣條函數法等。GPS重力高程方法則包括地球重力場模型法、重力場模型與GPS水準結合法、地形改正法等。具體應根據工區范圍大小及地形條件(比如平地、丘陵地、山地或高山地、等)選擇相應的有效方法。實踐證明,在局部GPS網中宜采用GPS水準高程擬合法(100 km2以內平坦地區平面擬合法的擬合精度優于4cm),在高程異常變化有規律的地區且已有控制點分布較均勻的情況下宜用二次曲面擬合法或高次多項式曲面擬合法(擬合精度可優于3 cm),大區域宜用重力場模型與GPS水準相結合的方法。

(1)平面擬合法

平面擬合法基本公式為

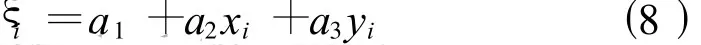
式(8)中,ξi為已知的某公共點(同時具有GPS大地高和國家高程的點)高程異常；xi、yi為某已知公共點相應的平面直角坐標；a1、a2、a3為待求的模型參數。當已知公共點為3時可直接求出a1、a2、a3值,若公共點的數目大于3則應采用最小二乘法解算a1、a2、a3,其相應誤差方程式為

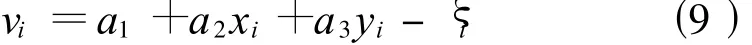
用矩陣的形式則可表示為根據最小二乘原理可求得

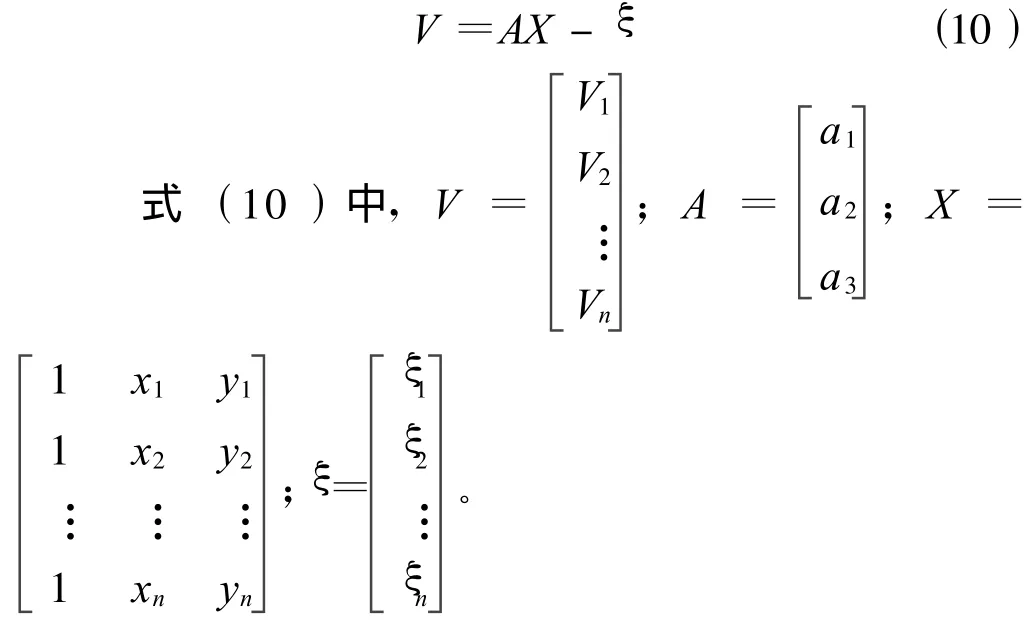
(2)二次曲面擬合法

二次曲面擬合法的基本公式為

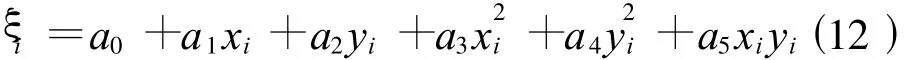
式(12)中 ,a0、a1、a2、a3、a4、a5為模型待定參數 ,不難理解,轉換區域內至少應有6個公共點。當公共點多于6個時,仍應組成誤差方程(見式(10))按最小二乘原理求解轉換參數 a0、a1、a2、a3、a4、a5。此時式(10)中的 X 、A 為

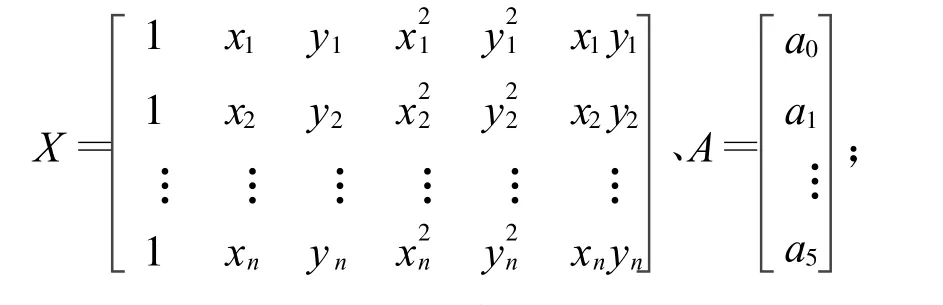
(3)高次多項式曲面擬合

高次多項式曲面擬合是二次曲面擬合法進一步擴展的結果,此時的數學模型為

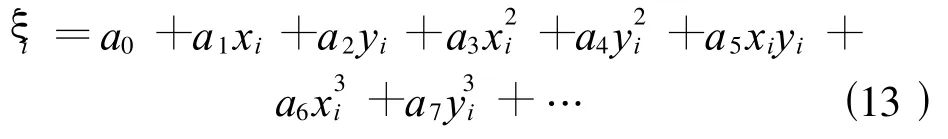
顯然,式(13)的誤差方程矩陣式仍可參照式(10)擴展列出。

(4)地球重力場模型與GPS水準結合法

方法的實質是在GPS水準點上,將由GPS大地高和水準正常高求得的高程異常 ξi與由重力場模型求得的高程異常 ξmi進行比較,求出其差值 δξi,即

然后再采用二次曲面擬合方法,由已知點的平面坐標(xi,yi)和 δξi推求其他點 K上的 δξk,進而可計算出待測點的正常高HK,計算公式為

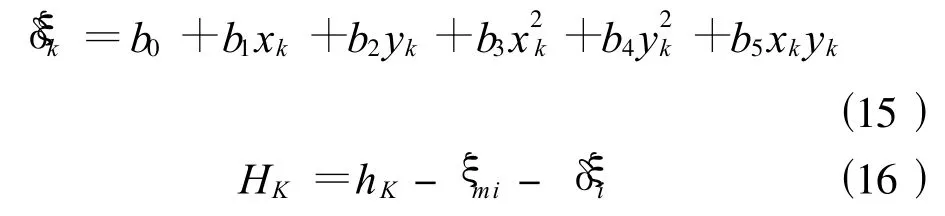
3.3 大地坐標(B,L)轉換為高斯平面直角坐標(X,Y)

換算數學模型(即高斯投影正算公式)為

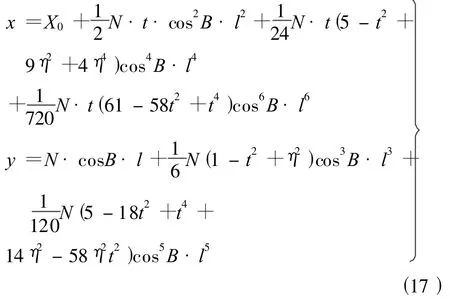
式(17)中,B為投影點的大地緯度；l=L-L0(L為投影點的大地經度,L0為軸子午線(中央子午線)的大地經度)；N為投影點的卯酉圈曲率半徑；t=tan B；η=e′cos B(e′為橢球第二偏心率 ,e′2=(a2-b2)/b2,a 、b分別為參考橢球的長、短半徑)。當l=0時,X0為從赤道起算的子午線弧長,其計算公式為

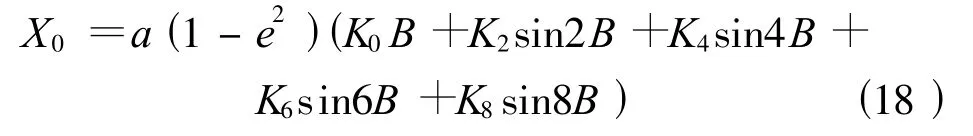
式(18)中 ,K0、K2、K4、K6、K8為系數 ,其中

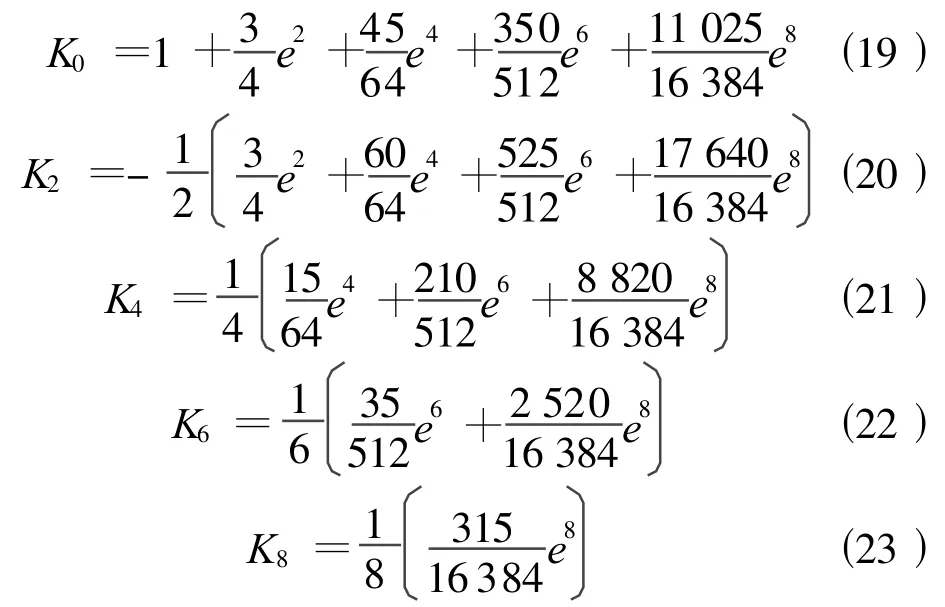
式(19)～式(23)中,e為橢球第一偏心率,e2=(a2-b2)/a2。

3.4 高斯平面直角坐標(X,Y)換算地理坐標(B,L)

換算的數學模型(即高斯投影反算公式)為

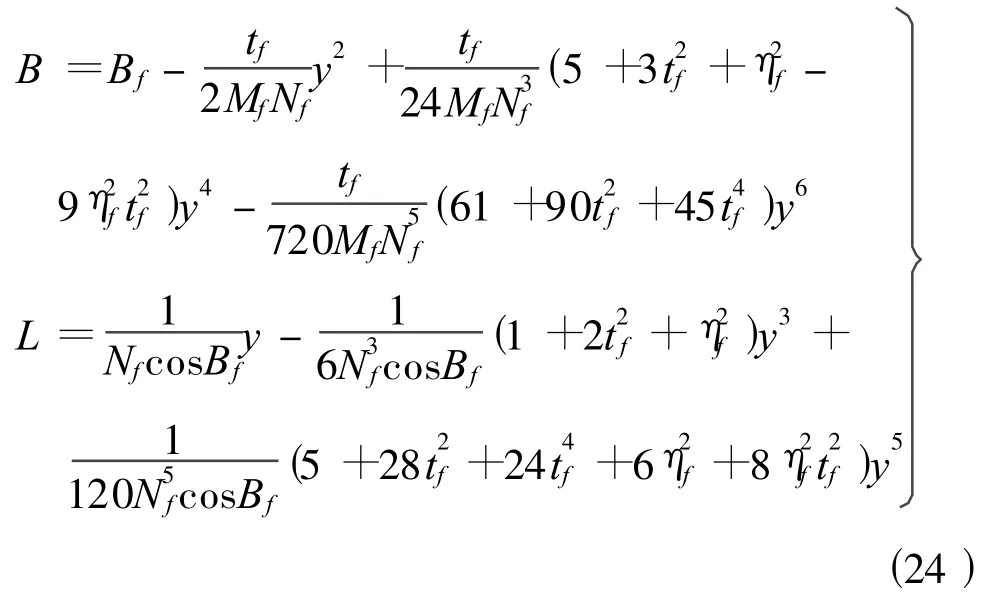
式(24)中,Bf為投影點的緯度(或稱底點緯度),其計算公式為

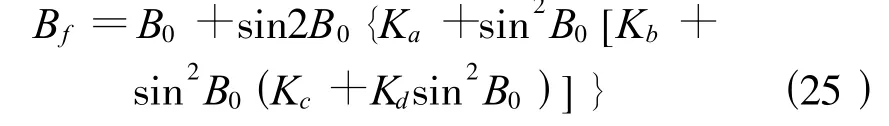
式(25)中,B0=X/[a(1-e2)A0](X為y=0時對應的子午線弧長)；Ka、Kb、Kc、Kd的計算公式為

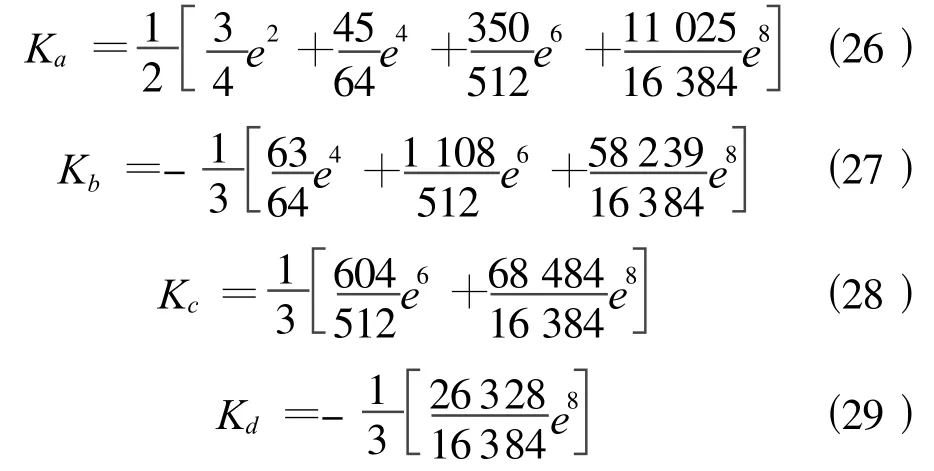
第一基本緯度函數W=(1-e2sin2B)1/2、第二基本緯度函數為 V=(1+e′2cos2B)1/2、B為大地緯度；子午圈曲率半徑為M=a(1-e2)/W3=c/V3；卯酉圈曲率半徑為N=a/W=c/V；平均曲率半徑為Rm=(MN)1/2=c/V2；任意方向法截弧的曲率半徑為 RA=Rm-[Rme′2cos B cos(2A)]/2=Rm+Δ(其中 A 為任意方向的方位角 ,Δ=-[Rme′2cos B cos(2A)]/2)。

3.5 坐標換帶

換帶的數學模型分2種情況,當 Δy1≤60 km時計算公式為

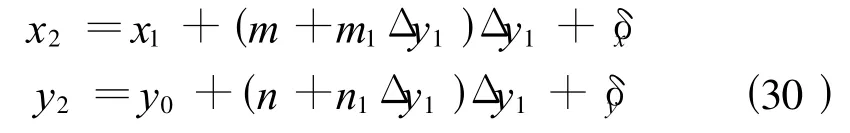
當 Δy1＞60 km時計算公式為

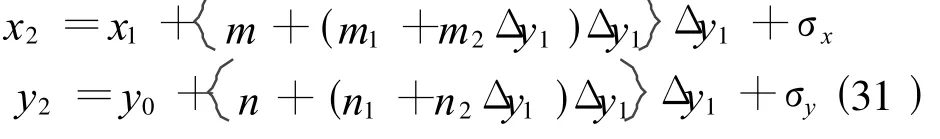
應用式(30)、(31)時,x1、y1為換帶前的已知坐標,x2、y2為換帶后的坐標,由西帶向東帶換帶時y2取負值,由東帶向西帶換帶時y2取正值。式(30)、(31)中,y0恒取正值；Δy1=±y1-y0(西帶換至東帶時y1前取 +號、東帶換至西帶時 y1前取取 -號)；δx=(4 γ0)-D sin(4 γ0)；m3=[5y0sin(2 γ0)]/(8R)；n=-

4 結束語

本文提出的鐵路線路歸一化放樣方法可極大地簡化鐵路線路放樣的過程,提高鐵路放樣的精度,為現代化測繪儀器(比如GPS、電子全站儀)在鐵路線路放樣中的便利應用奠定堅實的理論基礎,符合現代化放樣的歷史潮流。在應用本文所述方法時一定要分清各種各樣坐標系統、高程系統的特點及相互關系,一定要認真仔細地進行不同坐標系統、不同高程系統間的歸一化轉換,同時應注意滿足鐵路放樣中的精度要求,為鐵路的高標準、高質量建設提供優質的測繪保障。

注：本研究項目得到國家自然科學基金(79160173)的支持,在此表示感謝！

[1]鐵道部.高速鐵路隧道[M].北京：中國鐵道出版社,2006

[2]鐵道部.鐵路工程設計規范使用手冊[M].北京：中國鐵道出版社,2006

[3]劉統畏.建造師執業手冊：鐵路工程[M].北京：中國建筑工業出版社,2006

[4]李成輝.軌道[M].成都：西南交通大學出版社,2005

[5]郝 瀛.鐵道工程[M].北京：中國鐵道出版社,2000

[6]王午生,許玉德,鄭其昌.鐵路與城市軌道交通工程[M].上海：同濟大學出版社,2002

[7]張 未.跨區間無縫線路[M].北京：中國鐵道出版社,2001

[8]許實儒.軌道基本理論[M].北京：中國鐵道出版社,1999

[9]GB50308—1999 地下鐵道、輕軌交通工程測量規范[S]

[10]李青岳,陳永奇.工程測量學[M].北京：測繪出版社,1995

[11]GB50307—1999 地下鐵道、輕軌交通巖土工程勘察規范[S]

[12]TB10012—2001 鐵路工程地質勘察規范[S]

[13]CJJ8—99 城市測量規范[S]

[14]CH1002—95 測繪產品檢查驗收規定[S]

[15]CH1003—95 測繪產品質量評定標準[S]

[16]GB50026—93 工程測量規范[S]

[17]CH2001—92 全球定位系統(GPS)測量規范[S]