地方獨立坐標系與WGS-84坐標系轉換方法及應用
蔣小軍 宋占峰 吳清華
(中南大學土木建筑學院,湖南長沙 410004)
1 概述
城市道路是城市社會活動、經濟活動的紐帶和動脈,是城市綜合功能的重要組成部分,也是城市建設水平的集中體現。最近幾年,我國的城市化發展突飛猛進,城市基礎設施建設力度加大,城市道路的建設迎來了黃金時期,給城市道路的設計工作者既帶來了機遇,也提出了更新、更高的要求。傳統的城市道路設計理念或設計流程存在幾個方面的局限性:①線路設計在二維的地形圖上進行,地形地物的判別不直觀;②地形圖的范圍有限,設計人員的視野較窄,難以綜觀全局;③二維地形圖提供的信息有限,難以疊加區域三維建筑物、地質等重要信息。
近年來,隨著數字攝影測量技術、GIS技術、虛擬現實等高新技術發展,數字地球技術取得重要突破,以GoogleEarth為代表的數字地球軟件先后推出,為上述問題的解決提供了較好的途徑。GoogleEarth是擁有全球范圍豐富衛星影像和地形數據的三維數字地球平臺。這些衛星影像分辨率較高,現勢性較好,對道路規劃、方案評審、環境評估具有重要意義。
在城市道路工程的設計中,所使用的地形資料大多是在地方獨立坐標系下獲得的。為了將外業實測數據在GoogleEarth上進行三維表示,就必須實現地方獨立坐標與WGS-84之間的轉換,而地方獨立坐標系大都基于北京54坐標系建立的,所以一般以北京54坐標系為過渡坐標系,即地方獨立坐標系?北京54坐標系?WGS-84坐標系,三類坐標的橢球參數都不盡相同,必須使用相應的數學模型進行轉換。
2 橢球參數簡介
(1)WGS-84的橢球參數
橢球長半徑a=(6378137±2)m;
地球(含大氣層)引力常數 GM=(3 986 005×108±0.6 ×108)m3/s2;
正常二階帶諧系數 C2.0=-484.166 85×10±0.6 ×10-6;
地球自轉角速度 ω=(7292115×10-11±0.15×10-11)rad/s;
利用以上四個參數可以求出WGS-84橢球扁率f=1/298.257 223 563。
(2)北京54參考橢球(克拉索夫斯基橢球)
橢球長半徑a=6 378 245 m;
橢球扁率f=1/298.3;
地方參考橢球一般選擇與當地平均高程相對應的參考橢球,該橢球的中心、軸向和扁率與北京54參考橢球相同,其橢球長半徑則有一改正量 Δa,如圖1所示。
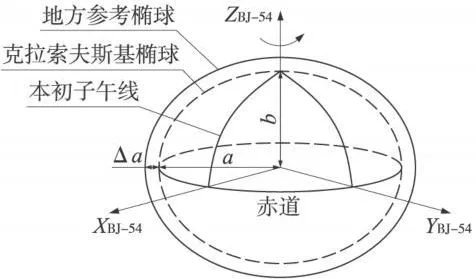
圖1 地方參考橢球與北京54參考橢球的區別
3 坐標轉換步驟及模型
坐標轉換流程如圖2所示。
3.1 同一參考系下的平面坐標轉換模型
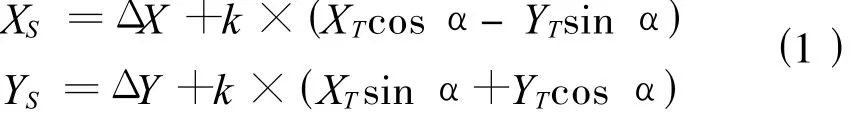
式中 ΔX、ΔY——x和y方向上平移系數;k、α——比例系數和旋轉角度。
3.2 布爾莎(Bursa)模型
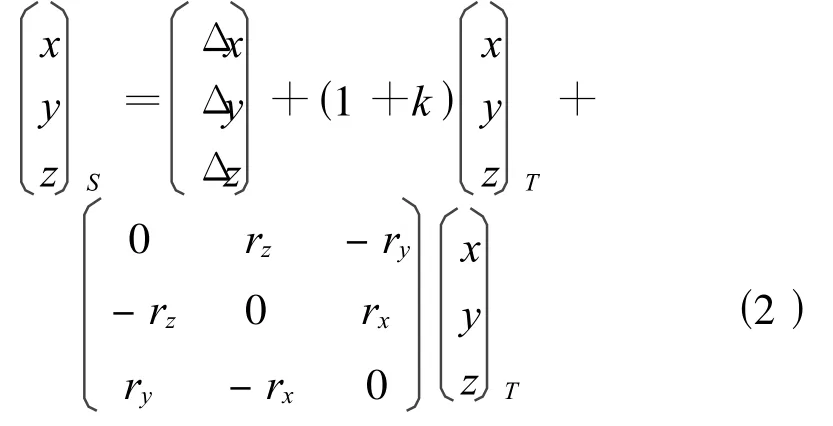
式中,Δx,Δy,Δz,k,rx,ry,rz為七參數。
考慮坐標數據的有效位數(32位操作系統上,C++語言的最高示數精度一般為15~16位),布爾莎模型在使用最小二乘法計算七參數的過程中將損失精度,故不能使用該模型直接計算七參數,但可用于確定七參數之后的回代計算。

圖2 地方獨立坐標系與WGS-84坐標系轉換流程示意
3.3 三維坐標差轉換模型
該模型是由布爾莎模型推導而來,假設有n(n≥3)個公共點,那么第 i(0 <i≤n,i≠j)個公共點坐標為(xi,yi,zi),第j(0 <j≤n,j≠i)個公共點坐標為(xj,yj,zj),設 Δxij=xj-xi,Δyij=yj-yi,Δzij=zj-zi,則三維坐標差轉換模型
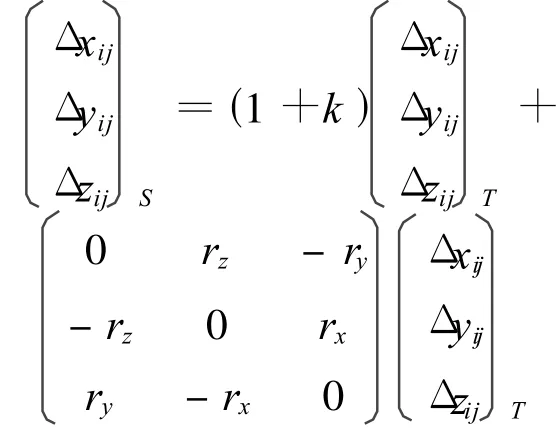
或
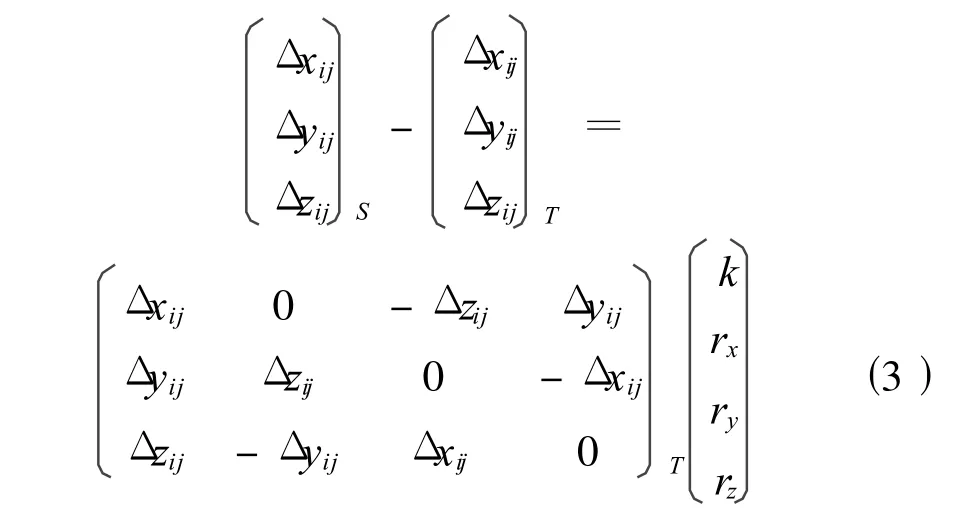
寫成矩陣形式為
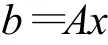
故求解該七參數可歸結為線性代數方程組的求解,對于這樣一類問題有多種求解方法,用的最多的是Gauss-Jordan消去法、正規方程組等。
在計算過程中,至少有兩個附加的因素會導致數值計算上的錯誤:
①雖然有些方程并非彼此精確的線性組合,但它們可能很接近線性相關,而在求解過程的某個階段,機器的舍入誤差使它們成為線性相關,這時計算程序將失敗。
②求解過程中,舍入誤差的積累也會使結果與真實解之間相差甚遠。這個問題在矩陣維數很大時特別容易發生,但計算進程在算法上并無錯誤。然而將結果直接回代到原來的方程就會發現,由它計算出來的x解集卻是錯誤的。由于求解過程中會不斷發生相近抵消,方程組越接近奇異,這種情況越易發生。事實上所計算的項可視為有效數字被全部舍去的特殊情況。
針對以上兩種數值計算錯誤,Gauss-Jordan消去法、正規方程組都是不穩定的。為了獲得高精度的七參數值,最好采用奇異值分解法。相比其他算法,奇異值分解的不足在于需要用額外的內存來存儲設計矩陣,且運算速度明顯要慢。但它最大的優點是:在理論上,它始終會得出有效的解集。
4 實例分析
以長沙市雨花路為例。長沙獨立坐標系的建立仍采用克拉索夫斯基橢球,中央子午線定在城市中央,為112°50′00.0000 ″E 。公共點坐標見表 1 。

表1 公共點坐標
4.1 四參數計算
長沙平面坐標轉北京54的四參數值為
x向平移:Δx=3 021 287.8529 m
y向平移:Δy=465 391.082 3 m
比例系數 :k=1.0 ×10-6
旋轉角度:α=-1975.224 3″
上述參數值由GPS測量提供,也可使用最小二乘法擬合公共點得出。
4.2 七參數計算
由于北京54坐標系下的大地高往往不能精確得出,同時實驗證明高程誤差對平面坐標轉換精度影響較小,故使用長沙獨立坐標系正常高代替北京54的大地高來解算七參數,從而得出七參數值(如表2所示)。

表2 轉換七參數
4.3 實驗結果
該算例中,AutoCAD圖形文件中房屋建筑所在坐標系統為長沙獨立坐標系,使用Google Earth二次開發技術,將長沙市雨花路數字地形圖轉換到Google Earth上,通過與Google Earth原有影像地形圖進行對比,所繪制的三維房屋建筑位置能夠很好的吻合已有的地形數據(如圖3所示)。
使用上述七參數進行轉換,在Google Earth中繪制三維建筑與線路(如圖4)。
5 結論
通過對地方獨立坐標系與WGS-84坐標轉換算法的介紹以及實例分析,可得出以下結論:
①地方坐標系下的高程異常一般無法準確獲得,同時高程誤差主要表現為對高程轉換精度的影響,而對平面坐標轉換精度影響較小。所以在解算七參數時,通常使用地方正常高代替北京54坐標系下的大地高,進行最小二乘擬合。
②從參數求解過程中及已知點回代誤差統計中可以發現,在已知點中存在個別粗差點,會扭曲與降低轉換參數的確定精度,所以最好將粗差點剔除后重新計算,以獲得更高精度的轉換參數。
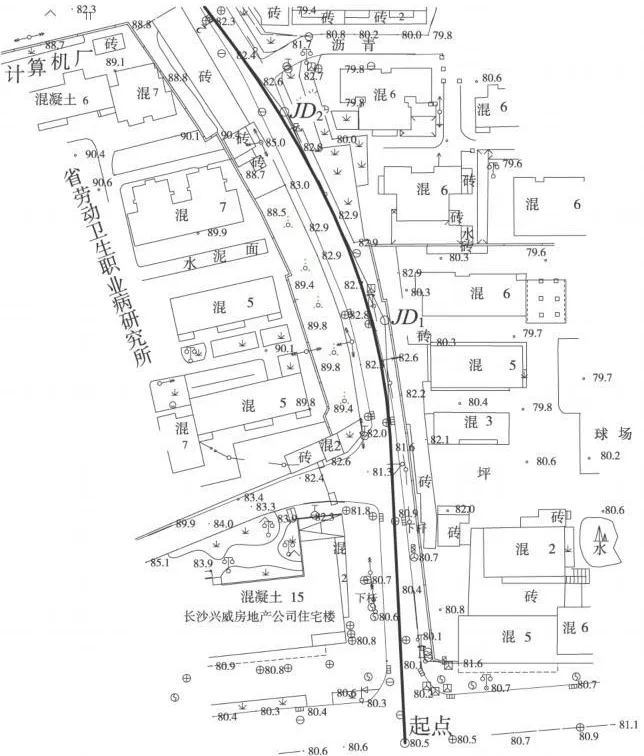
圖3 長沙市雨花路AutoCAD數字地形
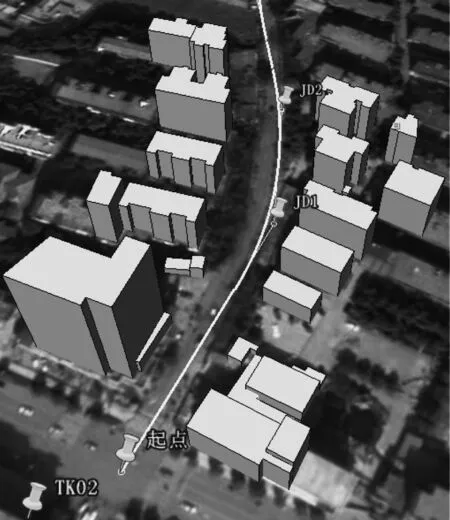
圖4 長沙市雨花路Google Earth三維地形
[1]趙長勝.高斯投影坐標反算的迭代算法[J].測繪通報,2004(3):16-17
[2]張曉帆,周可法,趙同陽,等.關于利用七參數法進行WGS-84和BJ-54坐標轉換問題的探討[J].測繪與空間地理信息,2007,30(5):33-42
[3]王解先,邱楊媛.高程誤差對七參數轉換的影響[J].大地測量與地球動力學,2007,27(3):25-38
[4]吳吉賢,楊志強,張耀文,等.BURSA模型應用于 BJ54與WGS84坐標轉換的討論[J].高原地震,2006,18(3):32-35
[5]張 勤,李家權.GPS測量原理及應用[M].北京:科學出版社,2005
[6]李征航,黃勁松.GPS測量與數據處理 [M].武漢:武漢大學出版社,2005
[7]孔祥元,郭際明,劉宗泉.大地測量學基礎[M].武漢:武漢大學出版社,2001
[8](美國)普雷斯,等著.胡健偉,等譯.C++數值算法[M].北京:電子工業出版社,2005

