結構參數變化對金馬大橋動力特性的影響研究＊

余報楚 邱文亮 余慶軍 李生勇 程曉紅

（大連海洋大學土木工程學院1） 大連 116023） （大連理工大學工業裝備結構分析國家重點實驗室2） 大連 116023）（福州大學橋梁工程研究所3） 福州 350002） （大連海洋大學海洋工程學院4） 大連 116023）

橋梁結構的動力特性包括自振頻率及主振型等［1］，它是橋梁計算的重要課題之一.橋梁結構的動力特性反映了橋梁的剛度指標，它對于正確地進行橋梁的抗震設計及維護，有著重要的意義.協作體系的固有振動特性的研究是其抗風、抗震及車輛活載所致的振動效應研究基礎［2］.斜拉橋與兩側連續結構協作后，結構剛度獲得提高，結構參與受力的程度得到加強，荷載的傳遞范圍得到擴大，結構的受力較普通斜拉橋趨于合理.本文從動力特性的角度出發，從廣東金馬大橋的動力特性分析入手，建立了廣東金馬大橋的動力有限元計算模型，對其進行了特征分析，并分別研究了各種結構參數變化對金馬大橋的動力特性的影響.

1 工程算例及有限元計算模型

1.1 工程算例及計算理論

金馬大橋位于廣東省廣肇高速公路上，橫跨西江，全長1 912.6 m，其中主橋為566 m，采用斜拉橋與剛構的協作體系，引橋為跨徑30 m的預應力連續梁橋.斜拉橋雙向對稱懸臂長223 m，兩側剛構雙向對稱懸臂長60 m，形成主跨為60 m＋283 m＋283 m＋60 m的跨徑組合（見圖1）.是目前世界上跨徑最大的混凝土斜拉橋與T型協作體系［3－4］，金馬大橋采用雙索面密索扇形布置，主梁標準斷面由兩側的實體邊主梁和間距4 m的橫隔梁組成梁格體系，橋面總寬28.6 m，梁上索距為8 m.兩側剛構采用雙箱單室截面，箱梁根部梁高8 m，端部梁高2 m，基礎采用雙薄壁柔性墩，滿足水平變位的要求.該橋283 m的主跨是世界上獨塔混凝土斜拉橋的最大跨徑.

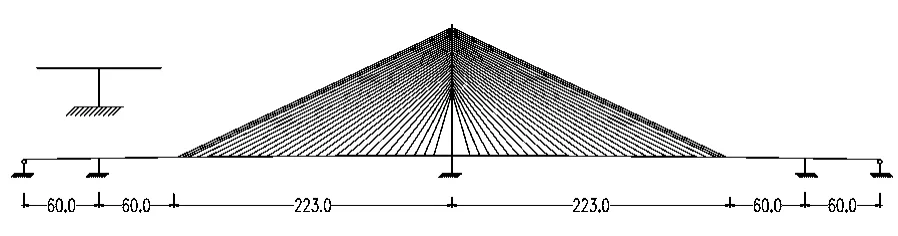
圖1 金馬大橋工程

對斜拉橋共振的分析和控制必須首先計算其頻率和振型.協作體系是一個空間三維結構體系［5］，在建立運動方程時，必須將其當作空間問題來考慮.根據有限單元法的基本原理將斜拉橋進行單元劃分，求出各部件空間梁單元的剛度矩陣和相應的質量矩陣，將它們轉換到總體坐標系中，并集成總體剛度矩陣和總體質量矩陣，分別記為K 和 M.設y＝｛x1，y1，z1，α1，β1，γ1，…，xn，yn，zn，αn，βn，γn｝T則斜拉橋體系的無阻尼自動振動方程為

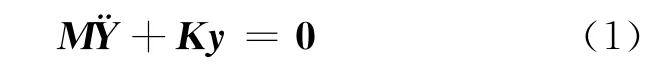
結構的自由振動由不同頻率的簡諧振動組成，取y為簡諧振動的形式代入上式，并在等式兩邊同乘以M－1，得

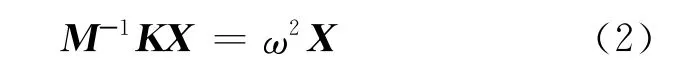
令M－1K＝P，則有

或者

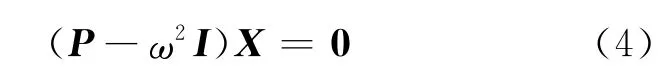
這是一個求解特征值的問題，該方程有非零解的充要條件，是其行列式為零，即：

該式稱為方陣p的特征方程.ω2j（j＝1，2，…，n）稱為方陣p的特征值或特征根，將所求的ω2j逐個代入式子（4）解出y，稱為方陣p與ω2j相對應的特征向量，也就是所要求的第j振型［5］.

1.2 空間有限元建模原則

該橋的主要受力構件有索、梁、塔、墩等，計算模型著重于結構剛度、質量和邊界條件的模擬.

1.2.1 橋梁構造的模擬 該模型邊主梁、塔柱和樁基礎采用空間梁單元模擬，為了準確模擬堆聚質量分布、振型形狀和地震力分布，主塔單元的劃分相對其它單元更為細密.橋面板和T構處的薄壁墩采用厚板單元模擬，承臺采用實體單元模擬，兩邊的大T構采用變截面梁單元，斜拉索采用只受拉桁架單元，索的彈性模量考慮垂度效應采用Er nst公式來進行修正.采用m法計算得到土彈簧剛度.

1.2.2 質量轉化與初拉力的考慮 橋面鋪裝設計時不做受力計算，即不與主梁構成整體一起承受結構內力，在建模時僅模擬鋪裝的質量，而不模擬其剛度，全橋為10 c m瀝青鋪裝，按均布荷載加載到橋面單元，然后將荷載轉化為質量.在高應力的纜索中，結構的面外剛度要大大的受到結構纜索的面內應力狀態的影響，這種面內應力和橫向剛度之間的耦合，稱為應力剛化.有限元數值計算分析中，將拉索索力加到對應的桁架單元，轉化為初始剛度矩陣，加到主剛度矩陣上.

1.3 有限元模型的建立

本文斜拉橋主橋為邊主梁結構，模型采用雙主梁模型，中間橋面板采用厚板與之相連，橫隔梁采用梁單元，連接方式是節點共用，計算模型共有3 009個節點，3 722個單元，其中梁單元為2 030個，板單元1 448個，實體單元132個，桁架單元112個，有限元計算模型圖如圖2，為了保證計算精度，進行反應譜分析時取前120階振型，采用CQC算法進行計算.采用遷移子空間迭代法.

圖2 金馬大橋的有限元模型

2 主要自振頻率和振型

計算得出金馬大橋的前20階自振頻率結果并與相同跨徑的普通斜拉橋（作為參照系的同跨徑的普通斜拉橋斜拉索的布置及形式，塔的幾何尺寸相同，梁體的截面幾何特性相同，所采用的計算方法相同，斜拉橋因為跨徑增至283 m，所以斜拉索長邊索增加了6對，共24根，塔柱高度也增加.同跨徑的協作體系與普通斜拉橋的自振頻率對比的計算結果比較如表1.

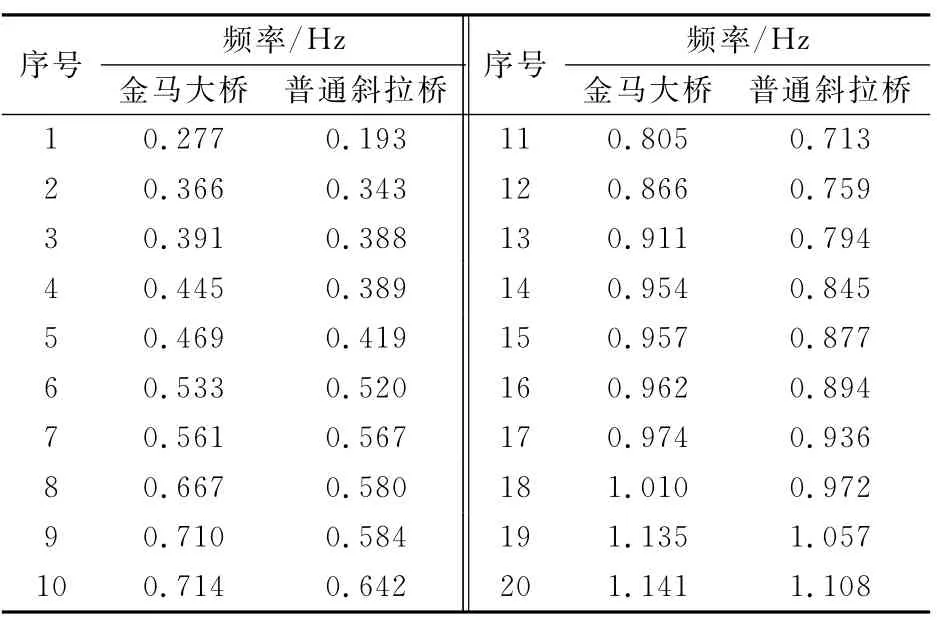
表1 同跨徑的協作體系與普通斜拉橋的自振頻率對比

3 結構參數變化對協作體系橋動力特性的影響研究［6－7］

分別計算了恒載、加勁梁剛度、塔架剛度、矢跨比等結構參數發生變化時廣東金馬大橋協作體系進行了動力特性的影響分析，并研究其規律.

3.1 恒載變化對動力特性的影響

當恒載按1.0，1.1，1.2，1.3，1.4，1.5，2.0倍率發生變化時，計算了金馬大橋的一階豎向、橫向和扭轉頻率的變化，見圖3.當恒載逐漸增大時，金馬大橋的豎向、橫向和扭轉頻率都在減小，豎向振動頻率減小幅度最大，恒載倍率由1.0增大到2.0倍，豎向振動頻率由0.277 4 Hz減小到0.217 1 Hz，扭轉振動頻率由0.444 5 Hz減小到0.341 2 Hz.

3.2 加勁梁豎向剛度變化對動力特性的影響

當豎向撓曲剛度按1.0～2.0倍率發生變化時，金馬大橋的豎向頻率逐漸增大，由0.277 4 Hz增大到0.365 6 Hz，而扭轉頻率和橫向振動頻率近乎保持不變.見圖4.

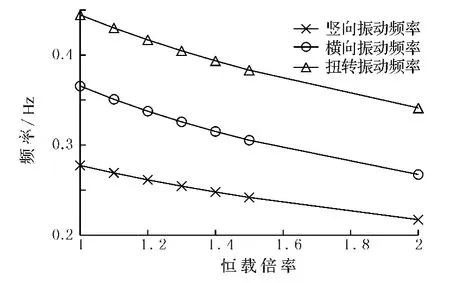
圖3 恒載變化對動力特性值的影響

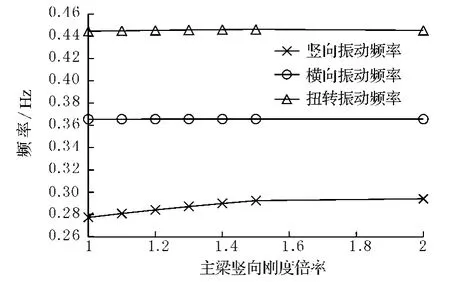
圖4 加勁梁豎向剛度變化對動力特性的影響

3.3 加勁梁橫向剛度變化對動力特性的影響

當橫向撓曲剛度按1.0～2.0倍率發生變化時，金馬大橋的豎向和扭轉振動頻率變化不很明顯，趨于穩定值，一階橫向頻率變化由0.365 6 Hz增大到0.377 7 Hz，見圖5.

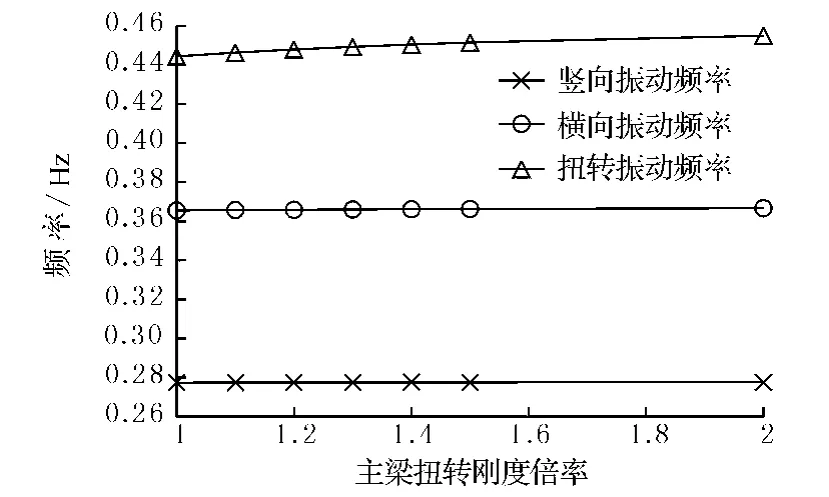
圖5 加勁梁橫向剛度變化對動力特性的影響圖

3.4 加勁梁扭轉剛度變化對動力特性的影響

當扭轉剛度按1.0～2.0倍率發生變化時，金馬大橋的豎向、橫向和扭轉振動頻率變化不很明顯，趨于穩定值，見圖6.

3.5 塔柱縱向剛度變化對動力特性的影響

當塔柱縱向剛度按1.0～2.0倍率發生變化時，金馬大橋的豎向和扭轉頻率稍有增加，變化不明顯，而橫向頻率幾乎不變，見圖7.

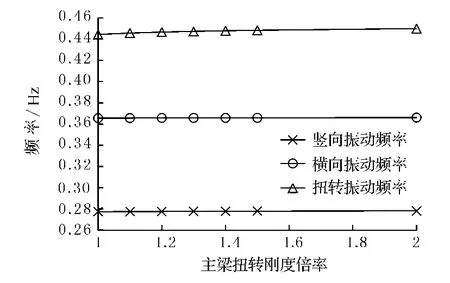
圖6 加勁梁扭轉剛度變化對動力特性的影響

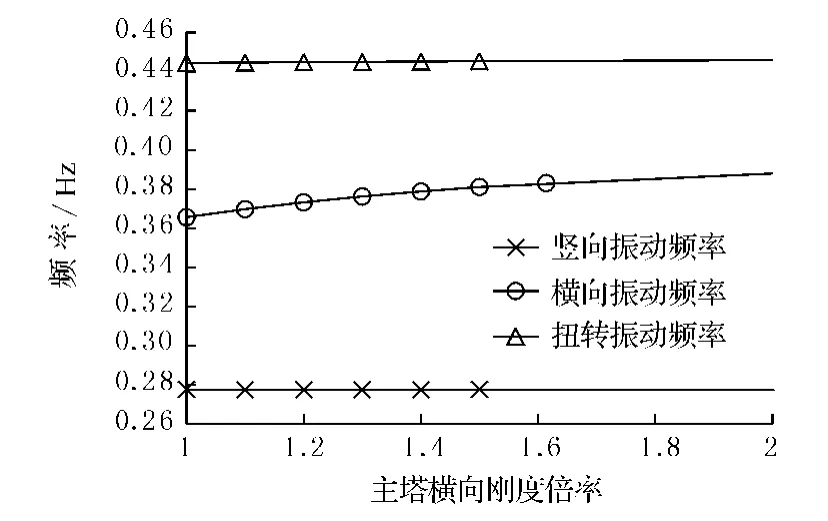
圖7 塔柱縱向剛度變化對動力特性的影響圖

3.6 塔柱橫向剛度變化對動力特性的影響

當塔柱橫向撓曲剛度按1.0～2.0倍率發生變化時，金馬大橋豎向，及扭轉頻率基本不變，趨于穩定值，只是橫向振動頻率呈增加迅速趨勢，見圖8.

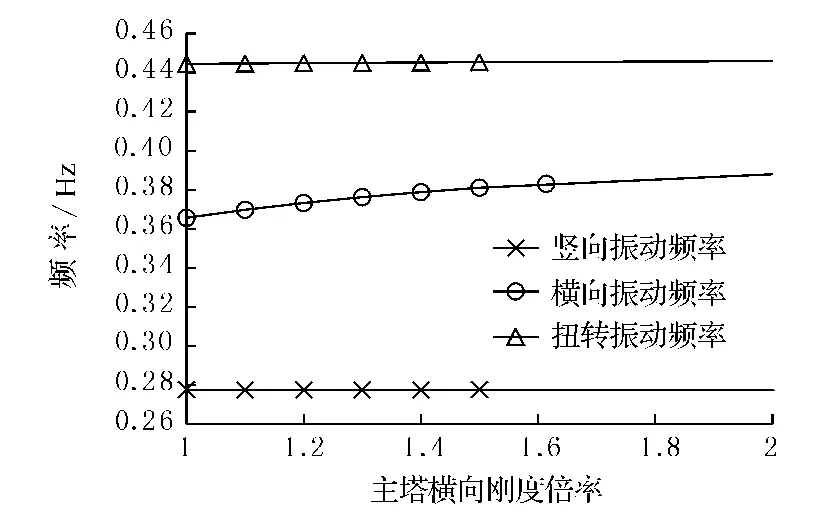
圖8 塔柱橫向剛度變化對動力特性的影響

3.7 斜拉索剛度變化對動力特性的影響

當斜拉索剛度按1.0～2.0倍率發生變化時，金馬大橋的豎向、橫向、扭轉頻率都呈增加的趨勢，扭轉振動頻率增加最快，其次橫向，再次為豎向，協作體系橋的一階豎向和扭轉振動頻率增加都比較快，分別由0.253 8 Hz增大到0.281 7 Hz和由0.445 9 Hz增大到0.476 9 Hz.

4 結 論

1）由于兩邊巨型T構的協作作用，金馬大橋的第一階周期為3.66 s，而同等跨徑的普通斜拉橋的一階周期為5.16 s，金馬大橋的整體剛度比同等跨徑的普通斜拉橋整體剛度要大，整體剛度得到了加強，同時在作初始幾何剛度荷載的分析的過程中，得益于較大的結構剛度，金馬大橋協作體系的拉索應力變化幅度相對于剪力鉸體系和普通斜拉橋都有較大幅度的下降，初始索力要更均勻一些.（因篇幅所限未列出的的成橋索力值），從而從動力特性剛度的角度上來分析表明金馬大橋現有的剛性協作體系設計非常合理.

2）振型較為密集.這種協作體系保留了傳統普通斜拉橋的特點，在這樣一個窄的頻帶上，許多振型都可能被激發，因此建議此對類似這樣的協作體系的地震反應分析應采取完全二次組合法（CQC法），而不能采取平方和開平方組合（SRSS法），否則導致結果不夠精確，同時建議在地震反應分析時要多選取一些振型.

3）增大加勁梁的豎向剛度使兩類協作體系橋的一階豎向頻率都有所增加，對金馬大橋非常明顯.增大橫向剛度對金馬大橋的一階橫向頻率影響很大，但是協作體系的豎向和扭轉頻率的影響不大.加大塔柱的剛度，對金馬大橋協作體系橋的一階頻率影響不大，對于金馬大橋，如果設計時能滿足承載力的要求，其剛度指標就會得到保證.隨著斜拉索的剛度只的增加金馬大橋的豎向、橫向、扭轉頻率都呈增加的趨勢，扭轉振動頻率增加最快，其次橫向，再次為豎向.

［1］李國豪.橋梁結構穩定與振動［M］.修訂版.北京：中國鐵道出版社，2002.

［2］陳仁福.大跨度懸索橋理論［M］.成都：西南交通大學出版社，1994.

［3］張 哲.金馬大橋設計實踐與理論探索［J］.大連理工大學學報，1993，39（2）：285－293.

［4］顏 娟.金馬大橋工程的結構分析與研究［D］.大連：大連理工大學，2002.

［5］范立礎.橋梁抗震［M］.北京：同濟大學出版社，2001.

［6］黃朝光，彭大文.單塔懸索橋的結構參數對動力特性的影響分析［J］.福州大學學報（增刊），1996，24（9）：279－287.

［7］陳 淮，郭向榮.大跨度斜拉橋的動力特性分析［J］.計算力學學報，1997，14（1）：57－63.