基于混沌機制PID控制器優化設計的研究

陳雯柏，張 鵬，劉景偉

CHEN Wen-bai1, ZHANG Peng2, LIU Jing-Wei3

（1. 北京信息科技大學 自動化學院，北京 100192 2. 河北建材職業技術學院 信息機電系，秦皇島 066000；3. 國電大渡河公司龔嘴水力發電總廠，樂山 614900）

0 引言

PID控制器結構簡單、易于實現，并具較強的魯棒性，被廣泛應用于各種工業過程控制中。PID控制器參數整定優劣與否，是其能否在實用中得到好的控制效果的前提。自Ziegler和Niehols提出PID控制器參數經驗公式法起，有很多方法己經被用于PID控制器的參數整定[1～4]。這些方法可按發展階段分為常規參數整定方法及智能參數整定方法。先進PID控制器參數整定方法給PID控制的研究帶來了活力。

PID參數整定實質是一組參數優化問題，選擇一個合適的算法，根據系統的性能目標函數，就可尋優到合適的PID參數。混沌是存在于非線性系統中的一種較為普遍的現象，混沌運動具有遍歷性等特點 ,它能在一定的范圍內按其自身規律不重復地遍歷所有狀態。本文采用梯度下降和混沌搜索相結合，完成PID控制器參數優化并成功應用于磁懸浮球控制系統。

1 混沌優化PID控制器設計

1.1 混沌優化

基于混沌理論的優化是一種新型的優化算法，它直接采用混沌變量在允許的解空間中進行搜索，搜索過程按混沌運動的自身規律進行，具有隨機性，易于跳出局部最小值，搜索效率高。因此，將混沌理論應用于控制系統的優化搜索中是近年來不斷探討的熱點問題[4,5]。

混沌優化算法的基本思想就是把混沌變量線性映射到優化變量的取值區間，然后利用混沌變量進行搜索。著名的Logistic(倍周期分岔道路)映射系統是目前研究的最深入的一個混沌系統模型，其動力學方程如式(1)所示：

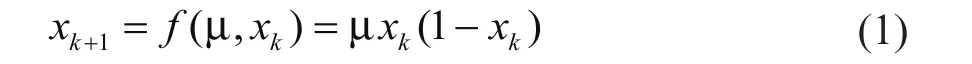
這里μ是一個控制參數，當μ大于3.57后，系統(1)開始出現混沌；當μ=4時，則完全處于混沌狀態，混沌變量x在(0,1)范圍內遍歷。混沌優化算法的特點是：1）結構簡單，有較高的執行效率；2）遍歷性特點中避免搜索過程陷入局部極小；3）不需要知道目標函數的導數信息；4）具有較少的計算量和較快的求解速度，調節參數可靈活控制計算時間和精度。

2.2 PID控制器參數尋優

PID參數整定實質是一組參數優化問題，選擇一個合適的算法，根據系統的性能目標函數，就可尋優到合適的PID參數。尋求PID控制最優參數是按照一定的尋優策略，不斷探測、調整，自動尋找最優的數字PID控制器參數，使得系統狀態處于最優狀態。PID控制器參數優化方法主要有以下兩種途徑：

1）基于現代控制理論的整定方法，寫出目標函數的解析式，然后根據目標函數取極值的充分必要條件，求出控制器參數的最優解。

2）基于一定的尋優算法，直接在參數空間中遍歷尋得最優參數值。

混沌PID參數尋優便屬于第二種途徑，其基本思想是：結合控制系統穩定的附加條件，利用混沌變量進行全局優化搜索PID參數最優解。用于PID控制器參數整定，尋優的目標函數必須與系統調節的性能指標函數密切相關，反映系統的調節品質。描述控制系統的目標函數并不是唯一的，常用的誤差性能目標函數有IAE、ISE及ITSE等[4]。

2.3 混沌PID控制器參數尋優算法

離散增量式PID表達式為：

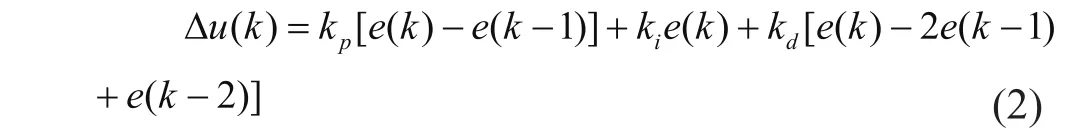
其中，T為采樣周期；k為采樣序號，k=1,2,...,N；u(k)為第k次采樣時刻PID控制器輸出的控制量；e(k)、e(k-1)分別為第k、(k-1)次采樣時刻輸入的偏差值；為積分系數，。由于混沌變量的變化范圍為(0,1)，而PID參數的變化不完全是(0,1)。可按式(3)所示進行變換將混沌變量映射“放大”為優化參數變量

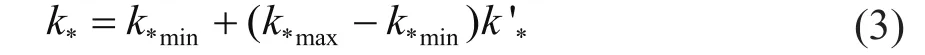
混沌優化具有全局搜索能力，但其局部搜索能力稍顯不足。基于梯度方向的確定性方法，雖具有收斂速度快的特點，但又容易陷入局部極值。因此采用混合優化算法先最速下降，再混沌搜索進行有機結合。為進一步提高搜索速度，文獻[6]提出一種改進的變尺度混沌搜索算法，本文應用并改動如圖1所示。實現尺度變換控制搜索半徑， λ控制變換的幅度。

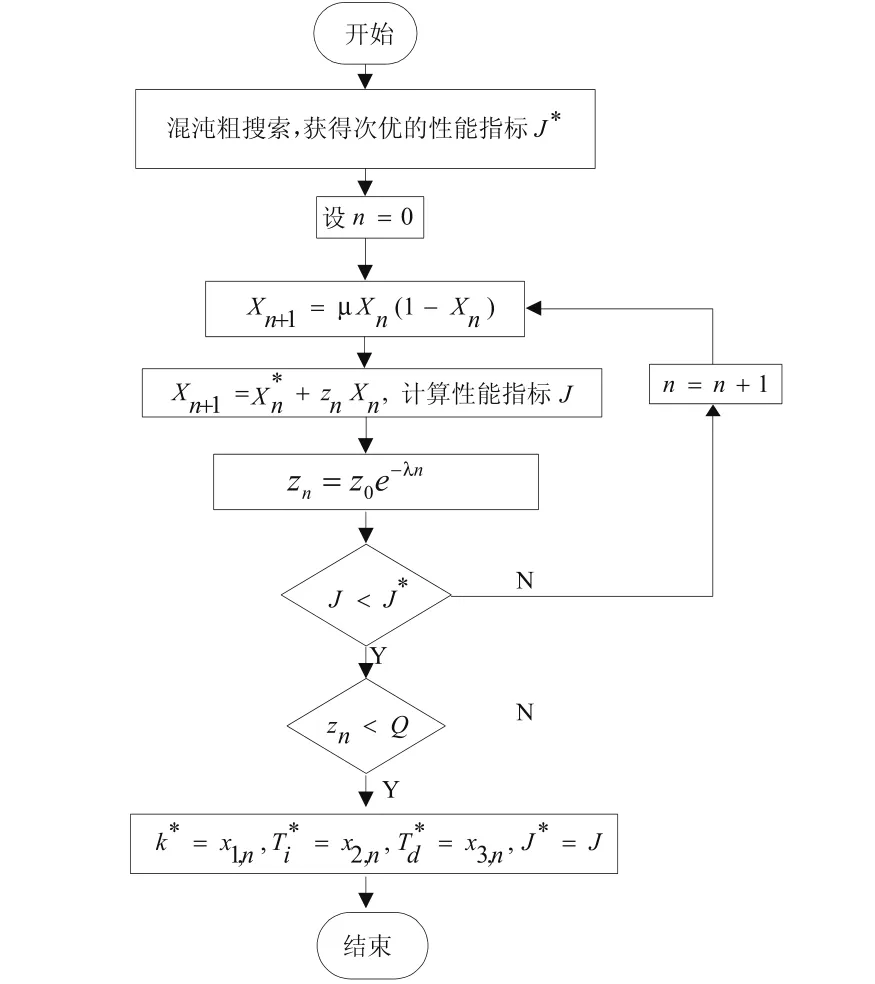
圖1 混沌優化算法的計算步驟

3 磁懸浮球系統的混沌優化PID控制

作為研究磁懸浮技術的平臺，磁懸浮球系統是一個典型的吸浮式懸浮系統，由鐵芯、線圈、位移傳感器、控制器、功率放大器和鋼球等元器件組成，其控制目標是通過調整加在電磁鐵線圈中的電流變化量i，使鋼球無接觸地穩定懸浮在空中。本文所研究磁懸浮球系統結構圖如圖2所示[7,8]。

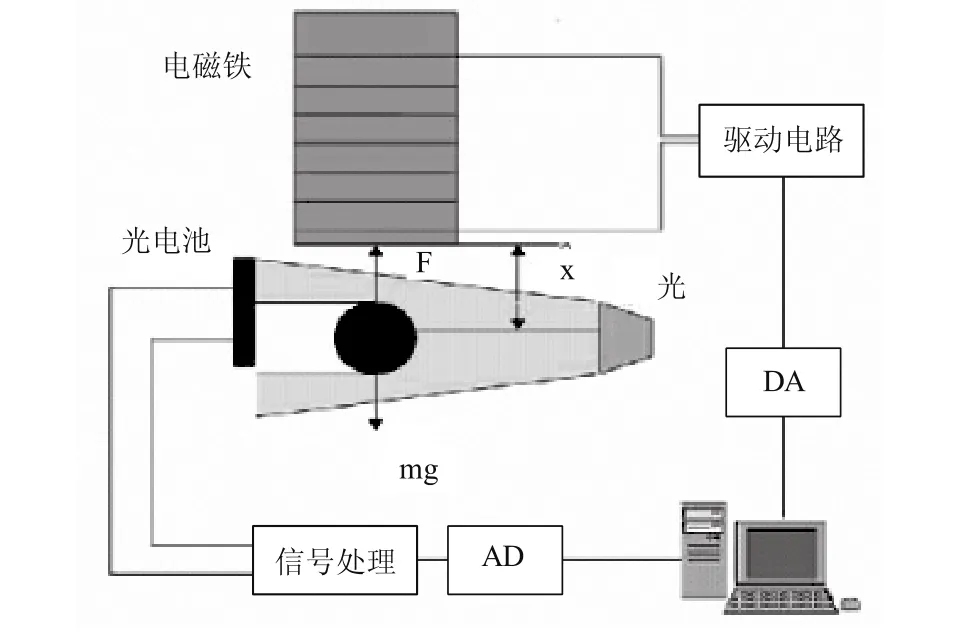
圖2 磁懸浮球實物系統結構

實際磁懸浮球系統的模型參數如下：鋼球質量m=22g，浮球半徑r=12.5mm，鐵芯直徑=22mm。忽略漏磁通，并假設磁通在氣隙處均勻分布，忽略小球和電磁鐵鐵芯的磁阻，假設球所受的電磁力集中在中心點，同時忽略小球受到的其他干擾力，在小球平衡點附近進行線性化處理。定義系統對象的輸入量為功率放大器的輸入電壓也即控制電壓Uin，系統對象輸出量為 所反映出來的輸出電壓Uout（傳感器后處理電路輸出電壓），則該系統控制對象的模型可寫為：

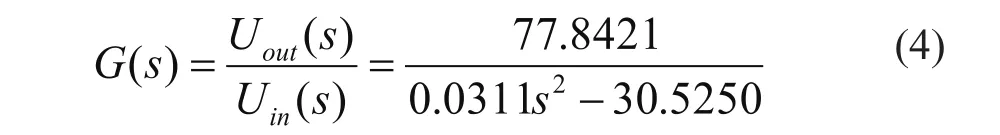
基于Matlab / Simulink的磁懸浮球實時控制系統結構如圖3所示，系統采樣周期T為0.003s。圖的左邊Pos Ref模塊給定了鋼球位置,通過Scope等模塊可以查看系統實時控制效果。

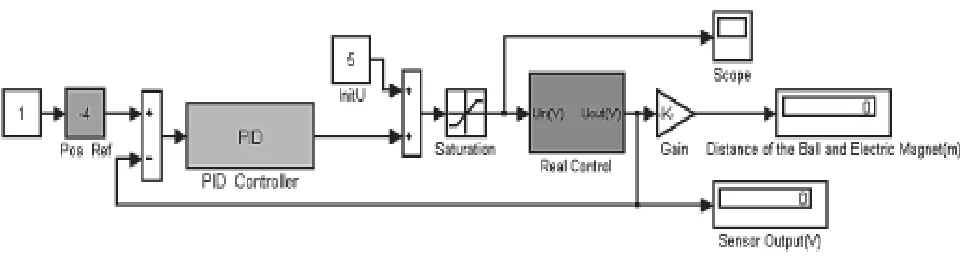
圖3 磁懸浮球系統的實時控制平臺

設定小球平衡位置為-1cm,采用傳統PID參數整定方法可得：kp=0.5，ki=0，kd=3，小球實際位移變化曲線如圖4(a)所示；在此基礎上，運用上述參數尋優方法得到的參數為：kp=0.4090，ki=0.000065，kd=4.1098，小球實際位移變化曲線如圖4(b)所示。

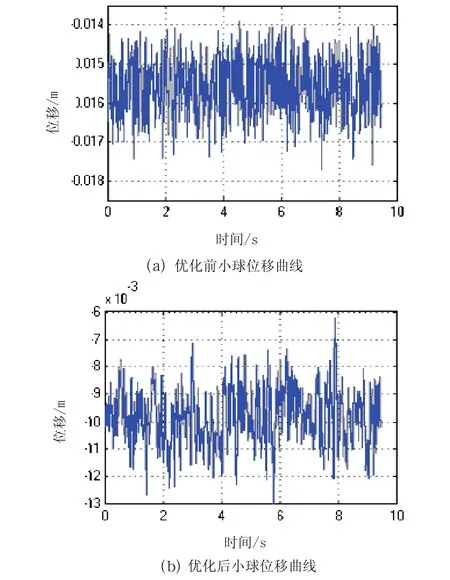
圖4 小球實際位移曲線比較

由圖4比較可知，在給定相同的位移 -1cm的情況下，采用混沌優化PID控制參數尋優后穩態誤差小，位移波動量也較小，取得了較好控制效果。這說明基于混沌優化方法的PID控制器設計是可行的。

3 結束語

混沌運動具有遍歷性特點,可應用于PID控制器的參數優化設計。本文首先對混沌優化的原理進行了簡單的介紹。接著，介紹了混沌PID控制器的參數優化設計的具體方法并進行了仿真研究。最后，針對實際的磁懸浮系統實驗設備，設計了PID控制器，并對優化前后進行了比較分析。本文說明了基于混沌機制的PID控制器參數優化策略可行且效果良好。

[1]劉樂星,毛宗源.水輪機的GA-PID控制器研究[J],電力系統自動化,Dec 1997,21(12)：41-43.

[2]K.H.Ang,G.Chong,and Y.Li.PID Control System Analysis,Design and Technology[J].IEEE Trans.on Control System Technology,2005,13(4)：559-576.

[3]Wang P,Kwok D P.Auto-tuning of classical PID controllers using an advanced genetic algorithm[C],Proc.of IEEE Int.Conf.on Power Electronics and Motion Control,San Diego,1992：1224-1229.

[4]李麗香,彭海朋,王向東,楊義先.基于混沌螞蟻群算法的P I D控制器的參數整定[J].儀器儀表學報,2006,27(9)：1104-1106.

[5]李祥飛,鄒恩,張泰山.基于混沌優化的規范化PID控制器及其應用[J].中南工業大學學報,2002,33(3)：301-304.

[6]鄒恩,陳建國,李祥飛一種改進的變尺度混沌優化算法及其仿真研究.系統仿真學報,2006,18(9)：2426-2428.

[7]固高科技.GML系列磁懸浮系統實驗指導書[Μ].深圳：固高科技(深圳)有限公司,2006.

[8]許良瓊,陸新江,李群明.模糊PID控制在磁懸浮平臺中的應用[J].中南大學學報(自然科學版)：2005,36(4)：631-636.