基于粒子群算法優化的目標識別方法

侯亞麗,李 崗,王 偉

(機電工程與控制國家級重點實驗室,陜西西安 710065)

0 引言

目標識別是指從接收到的目標散射回波(如微波、紅外線、可見光、激光、超聲波)中提取目標的有關信息和穩定特征進而判明目標屬性的一門技術,在軍事信息處理領域中有重要的應用意義。隨著目標識別理論的發展以及軍事目標高識別率的要求,目標識別系統的設計也越來越復雜,這就需要提取目標足夠多的信息來反映目標特征,從而進行識別。各種利用優化算法改進BP網絡的目標識別方法紛紛出現[1-2]。Levenberg-Marquardt(LM)方法[1]是一種快速收斂算法,在改進BP網絡上表現出較好的性能;但是,LM算法旨在提高網絡收斂速度,本質上還是基于梯度下降原理的,必然存在局部極小點,從而不可避免地陷入局部極值[3]。所以為了避免這種情況,本文采用了基于優化理論的粒子群優化算法(PSO)來改進LM 算法。

1 算法原理

目標光散射的瞬態特性是近幾年發展起來的研究目標光散射特性領域的一個方向。它是指對目標進行全照射時,目標在瞬間反射的光信息的特性,不僅包含了速度、方位、距離等信息,還可以從中提取更具體的特征信息,如目標姿態、尺寸、材料等。利用這些信息,提取目標特征并處理,可作為目標識別領域的一種新方法,本文針對提取目標特征后的識別算法進行研究。

根據特性量及特征矩陣的結構,選取的BP網絡結構為3-7-3,如圖1。輸入量是對目標瞬態特性進行奇異值特征提取后的一維向量,長度為3,輸出量是歸一化后數值在0.1～0.9之間的一維無量綱向量。

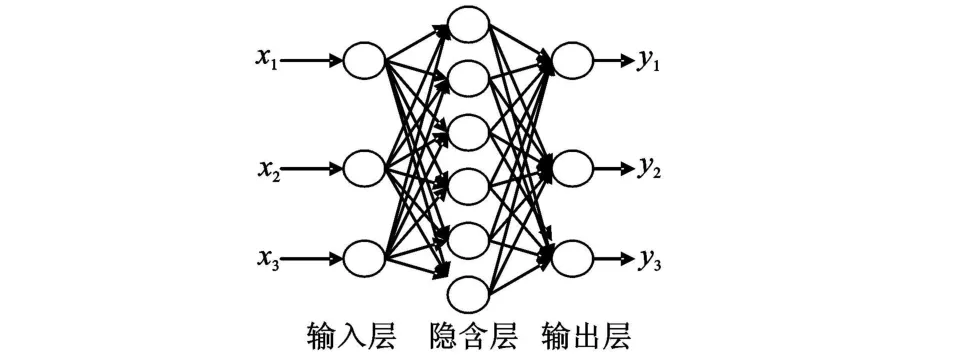
圖1 BP網絡結構圖Fig.1 BPalgorithm frame

LM算法是一種基于BP網絡的快速收斂改進算法[2],能在網絡收斂速度上得到大大的提高,這是LM算法最大的優點,但是究其原理仍然是基于梯度下降法,就不可避免地會出現局部極值;另一方面,根據文獻[4]及本文利用LM算法的識別結果,對權重敏感、精度不高等問題也會對網絡的識別率產生影響。

2 粒子群算法

PSO算法具有較強的全局收斂能力和較強的魯棒性,將其與快速收斂算法結合,不僅能提高收斂速度,克服網絡陷入局部極值的缺點,在識別精度上也會有較大改善。算法原理描述如下[5]:

設Xi=(xi1,xi2,…,xin)為微粒i的當前位置,Vi=(vi1,vi2,…,vin)為微粒i的當前飛行速度,Pi=(p i1,pi2,…,pin)為微粒i所經歷的最好位置,對最小化問題,目標函數值越小,對應的適應值越好。

設f(X)為最小化的目標函數,則微粒i的當前最好位置為:

設群體中的微粒數為s,群體中所有微粒所經歷的最好位置為Pg(t),稱為全局最好位置。則

基本微粒群算法的進化方程為:

式中,w(t)為慣性權值,通常隨進化代數從0.9線性遞減至0.4;下標j表示微粒的第j維,i表示微粒,t表示代數,c1,c2為加速常數,通常取 2,r 1～U(0,1),r2～U(0,1)為兩個相互獨立的隨機分布。

從上式看出,c1調節微粒飛向自身最好位置的步長,c2調節微粒飛向全局最好位置的步長,vij為減小微粒離開搜索空間的可能性,限定在一定范圍內,即

將訓練好的網絡權重值作為LM算法初始值,按照LM算法步驟,進行目標識別,具體流程如下。

用PSO訓練神經網絡時,定義粒子群的位置向量X元素是BP網絡的全體連接權值和閾值,首先初始化向量位置X,然后用PSO搜索最優位置,求

的誤差(適應度)最小值。其中,tjk是目標值,f jk是計算值,m是輸出節點數,ns是訓練集樣本數。算法流程如圖2所示。

圖2 PSO算法流程Fig.2 PSO algorithm flow chart

3 算法識別性能驗證

3.1 改進算法實例

本文選取檢驗樣本的450組數據對其進行訓練,優化前后的步長-誤差效果圖如圖3、圖4所示。圖中,橫坐標表示訓練步長,縱坐標表示訓練誤差范圍。

圖3 LM算法訓練BP網絡結果Fig.3 BP result training by LM algorithm

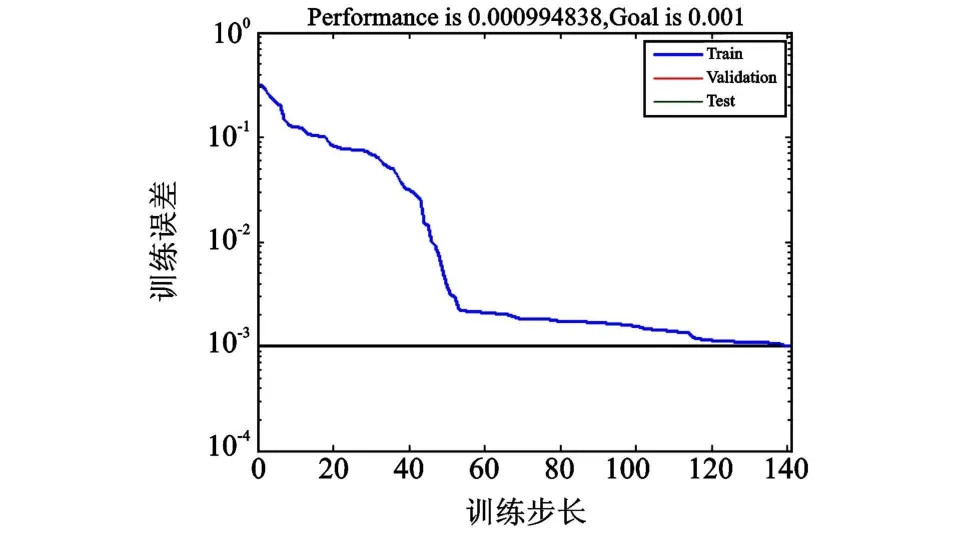
圖4 PSO優化LM算法結果Fig.4 LM result optimized by PSO algorithm

可看出,當步長為202時,LM算法即達到所需精度,是一種收斂較快的算法,單從這一方面來講能夠滿足識別要求;但訓練過程中速度越來越慢,甚至在接近誤差精度時趨向平坦,這說明算法可能收斂于局部極值,對識別效果上會產生影響;PSO算法優化后的LM網絡不僅具有較快的收斂速度(141步),而且克服了誤差下降時的平坦區,使誤差快速、穩定的減小到極值,這是比較理想的輸出結果。

隨機選取20組樣本進行識別,結果如表1和表2。

表1 LM算法優化的BP網絡的識別結果Tab.1 Identify results of BP optimized by LM algorithm

表2 PSO算法的識別結果Tab.2 Identify results of PSO algorithm

3.2 結果分析

表3 LM、PSO算法的比較Tab.3 Compare LM algorithm with PSO

從表3可以看出,利用神經網絡實現對目標的光散射瞬態特性進行目標識別時,PSO優化后的算法優于LM 算法,具體表現在:

1)在識別速度方面,PSO學習算法的收斂速度有所提高,收斂時間有所減少,這一點可以從訓練步長的大小看出(LM算法對整個樣本的識別步長是202,PSO優化后的步長是141)。

2)在識別精度方面,PSO學習算法的全局優化能力使LM算法的局部收斂問題得到解決,克服了LM算法對初始權值敏感,容易陷入局部極小的缺點,從而分類效果較好,識別率較高,其泛化能力較強,是比較理想的一種目標識別算法。

這是因為PSO算法簡單,計算復雜度低。在對空間的搜索過程中,通過群體信息的共享加速了收斂速度,縮短了下降時間,將PSO的宏觀搜索能力與BP算法的指導性搜索思想相結合,同時利用LM算法的快速收斂功能,發揮各個算法的優勢,解決了LM算法容易陷入局部極小的問題,且收斂速度快。將訓練后的網絡對識別樣本集中的樣本進行識別,識別正確率較高,說明用PSO算法訓練的神經網絡具有很好的泛化能力。

4 結論

本文提出了基于粒子群算法(PSO)權值優化的LM算法,通過對這算法的分析比較,從識別結果可以看出本文提出的改進方法達到了目標識別的要求,不僅提高了網絡的學習速度,還提高了網絡的學習精度,克服了基于梯度下降法的LM算法易陷入局部極值的缺點,優化后算法的識別精度滿足軍事目標識別的需要,為利用目標特性進行目標識別提供了有力的理論支持。

[1]BP網絡的改進算法簡介[EB/OL].研學論壇,(2006-10-28)[2009-12-03].http://bbs.matwav.com/viewthread.php?tid=583816.

[2]飛思科技.MATLAB6.5輔助神經網絡分析與設計[M].北京:電子工業出版社,2003.

[3]侯亞麗,李鐵.基于LM優化算法的BP神經網絡目標識別方法研究[J].探測與控制學報,2008,30(1):53-57.HOU Yali,LI Tie.Improvement of BP neural network by LM optimizing algorithm in target identification[J].Journal of Detection&Control,2008,30(1):53-57.

[4]王麗霞.一種前饋神經網絡算法[EB/OL].(2004-10-24)[2009-12-03].http://www.docin.com/p-8944092.html.

[5]曾建潮,介婧,崔志華.微粒群算法[M].北京:科學出版社,2004.