合理構造函數 化解教學疑難

●劉官茂 (寧波萬里國際學校中學 浙江寧波 315040)

函數在高考中不僅占有較大比重，而且在新課標中也處于非常重要的地位.函數是聯系代數與幾何、定量與變量的橋梁和紐帶，是中學數學的主干知識之一，是學好中學數學的關鍵.利用導數和函數的性質解決各種綜合問題是高考的重點、熱點和難點.本文試圖通過合理構造函數化解教與學中的一些疑難問題，加強對函數本質的理解，提高函數思想的應用意識.

1 合理構造函數

1.1 根據函數性質，合理構造函數

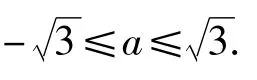
分析看到該題的第一反應是求導，利用切線與割線的斜率關系直觀地闡述，或補充高等數學中的拉格朗日中值定理說明，這顯然都是不合理的.要想化解這個疑難，只需設 A(x1，y1)，B(x2，y2)是函數圖像上任意不同的2個點，則

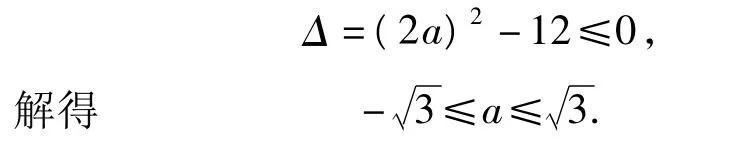
評注如果題目中涉及到曲線任意2個點的斜率范圍，那么均可以按照此法來構造函數，把問題轉化成函數的單調性問題，進而用導數順利突破.解題過程清晰、自然，體現了轉化化歸的思想.

1.2 化定量為變量，合理構造函數

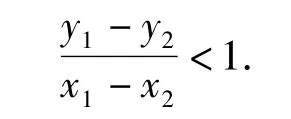
例2 當0＜a＜b時，求證：顯然 x1≠x2，不妨設 x1＜ x2，則

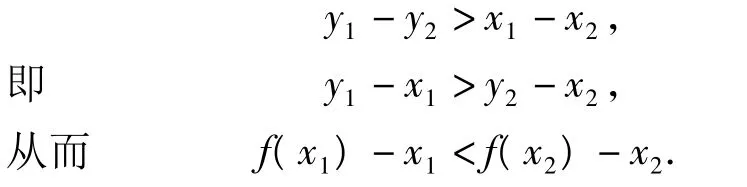
由函數的單調性可知，只需構造函數 g(x)=f(x)-x，則 g(x)在 R上是減函數，g'(x)=-3x2+2ax-1≤0在R上恒成立，故

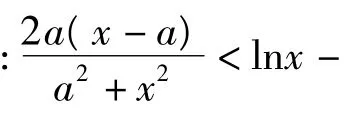
評注對于多元不等式的證明問題，可以采取這種化定量為變量，合理構造函數的方法解決.

1.3 根據消元轉化，合理構造函數

例3 已知函數 f(x)=lnx，g(x)=ax2-x(a≠0)，若函數y=f(x)與y=g(x)的圖像有2個不同的交點M，N，且過線段MN的中點做x軸的垂線分別與f(x)的圖像和g(x)的圖像交于點S，T，以S為切點作f(x)的切線l1，以T為切點作g(x)的切線l2.問是否存在實數a使得l1∥l2?如果存在，求出a的值;如果不存在，請說明理由.

分析此題入手易，深入難.設點M(x1，y1)，N(x2，y2)，由 l1∥l2可得

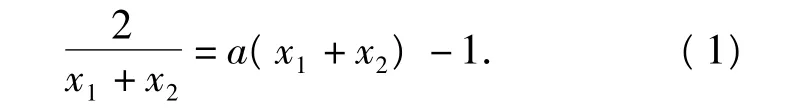
接下去，學生基本上沒有思路了.通過適當消元轉化則能迎刃而解.首先對式(1)兩邊同乘以x1-x2，得

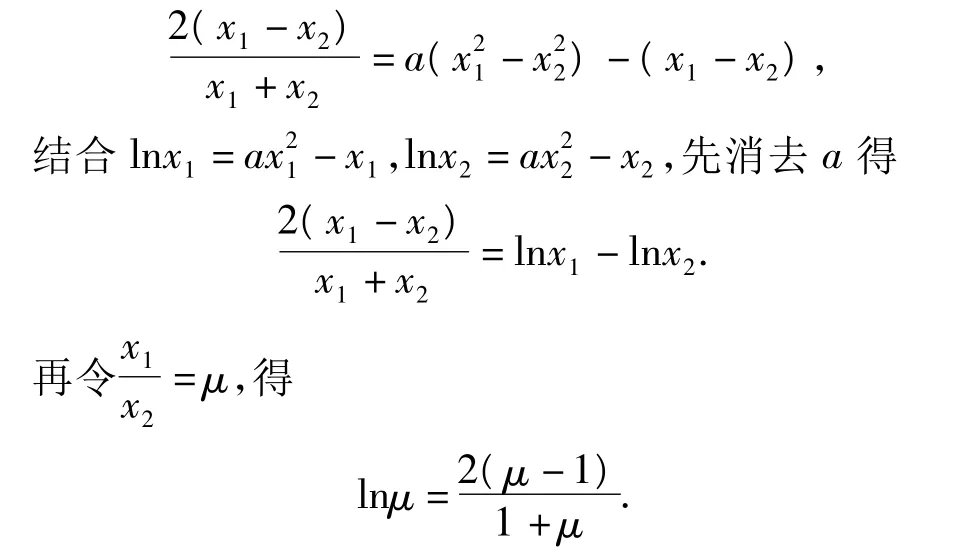
評析 此題通過2次合理消元，最后把問題蛻化為一元函數，通過求值域解決問題.對于多個變量問題，應理清變量間的關系.

2 利用函數如何化解疑難問題

2.1 利用函數性質化解疑難

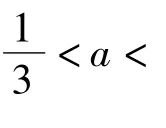
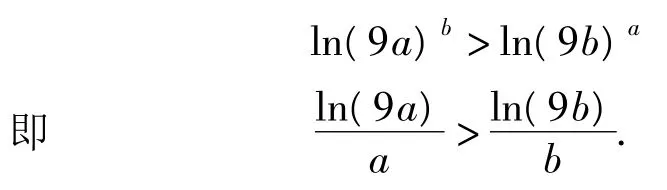
評注導數的引入后，不等式的證明多了一條出路，函數的單調性往往蘊含著大小的比較問題，合理構造函數利用單調性即可證明.

2.2 巧用數形結合化解疑難

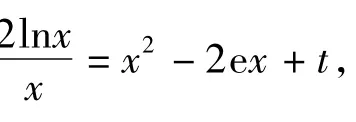
評注本題最主要的特點是對方程進行了重新“配置”，而關鍵點就是配置后左右2邊對應的函數有相同的極值點，進而利用函數的圖像分析解決問題.一般來說，對于比較復雜的方程求根或是判定函數零點的個數問題.要善于發現方程的結構特征，對方程的結構進行分離重配，轉化為一邊是熟悉的基本函數形式，另一邊可以是較復雜的函數形式，用導數對函數的變化趨勢進行研究.最后把根的個數問題轉化成2個圖像的交點個數問題.

2.3 妙用降維化歸化解疑難

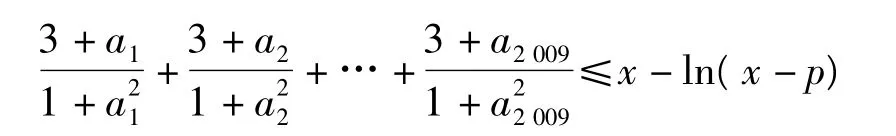
在x∈(p，+∞)時恒成立，求實數p的最小值.

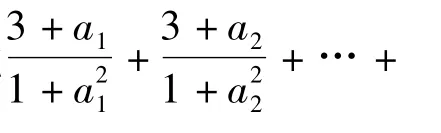
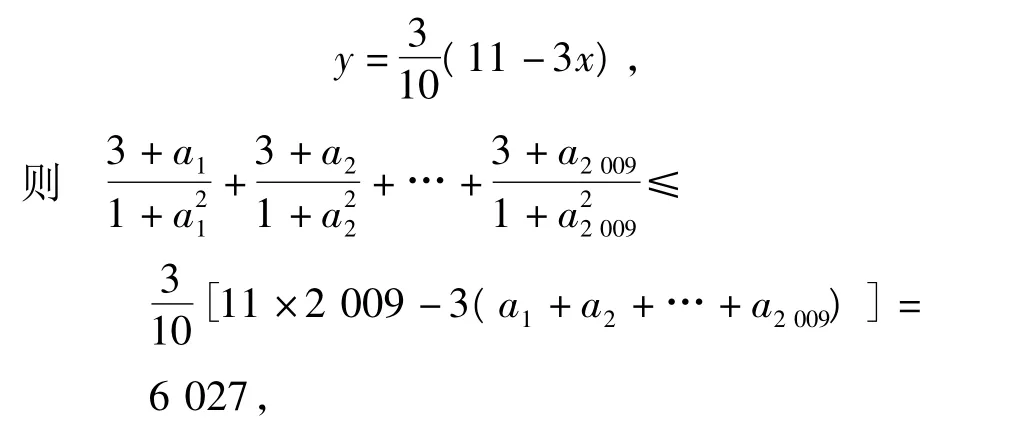
接下來，可求得x=ln(x-p)的最小值為p+1，因此 p≥6 026.

評注對于比較難化簡的求和形式，一般是通過放縮或轉化得到比較容易的函數形式.

在解題教學過程中，要向學生暴露思維過程，對解題切入點或突破口的選擇要舍得花時間分析引導，問題解決中“坎”的跨越、“陡坡”的攀登要濃墨重彩.題目的講評不是一味地呈現標準答案，要從學生解題“卡殼”的難點處著手突破，幫助學生解決問題，并和標準解法進行比較分析.解題后要關注反思和拓展，品味解題的方法和關鍵點，探索一題多解，深入理解數學本質.

難題的講解一定要在關鍵點上突破，在學生的疑難點上啟發，通過題組與變式的練習，強化學生的解題經驗.