基于穩定性的FAST TCP參數γ調整

梁偉，張順頤，寧向延，徐蘇磊

（1. 南京郵電大學 信息網絡技術研究所，江蘇 南京 210003；2. 常熟理工學院 計算機科學與工程學院，江蘇 常熟 215500）

1 引言

關于擁塞控制的研究工作當中，除了平穩狀態性能分析，另一個主要就是擁塞控制算法的動態性能分析。尤其是要考慮不計反饋時延時的穩定性，以確保系統工作狀態的確是趨于平衡的[1]。FAST TCP是在Vegas基礎上采用反饋時延作為擁塞度量的改進方案，目的是解決高速大時延環境下傳統算法帶寬利用率不高的問題[2]。在高速網絡環境下，帶寬利用率可達90%以上，這一點是其他算法所無法比擬的。FAST根據距離平衡點位置的遠近非線性地調整窗口大小變化的快慢，以此提高窗口的響應速度和減緩窗口的波動幅度，使得數據流始終處在最佳傳輸狀態。直到最近2年才出現了對FAST穩定性能的實驗探索和理論研究，在FAST TCP中參數γ是數據源控制強度，對網絡性能有顯著影響，而其設置范圍的研究工作還遠遠不夠。文獻[3～6]提到相關的工作。在文獻[7]中，對影響穩定的微觀因素做了探討，分析了2個RTT有差別的FAST數據流共享一條瓶頸鏈路時的穩定情況。文獻[8]采用離散時間鏈路模型，推導了FAST的局域漸趨穩定的條件。文獻[9]提到了一個數據源在一條瓶頸鏈路傳輸時，FAST的參數α、γ對穩定性的影響，有待于進一步分析多個數據源共享一條瓶頸鏈路的穩定情況。文獻[10]應用Lyapunov函數分析了穩定條件，也是局限于一個FAST數據流傳輸的情況。在文獻[11]中，參數 γ的值限定在(0,1]，在文獻[12]中推薦γ設為0.5，在文獻[13]中，γ的條件分析不夠全面不夠深入。

針對以上不足，本文對FAST TCP的穩定性進行深入探討，目的是得出參數γ的邊界條件。本文從分析穩態流量FAST負反饋模型來解決這個問題的，具體分析了1個數據流，2個數據流在一條瓶頸鏈路上傳輸時，網絡的FAST參數γ的設置是如何影響穩定的。本文也對于一條瓶頸的鏈路上傳輸無數條數據流的情況作出了證明。

2 數學模型

2.1 網絡流量模型

考慮在一條容量為C的瓶頸鏈路上有多條TCP數據流進行傳輸，如圖1所示。各TCP流依次記為在本文中用p表示鏈路的排隊時延，wn表示數據流 n的擁塞窗口大小， xn表示排隊隊列中數據源n的數據到達率，dn表示數據流n的鏈路傳播時延，τn表示數據流n的往返時延RTT，其中它們均為時間t的函數，不帶t加小括號的時候表示該變量平衡狀態的值。設τnf為前一段鏈路傳播時延，即從數據源n到瓶頸鏈路的傳播時延。相應地，τb( t )為數據分組到達瓶頸鏈路后到

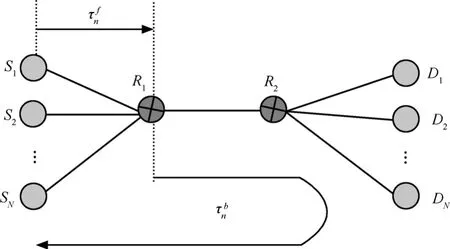
圖1 TCP連接拓撲

n

研究表明基于窗口的擁塞控制假定發送速率與窗口大小除以往返時延成比例，把排隊隊列看成一個簡單的積分器，對鏈路上大于鏈路容量的傳輸速率進行積分，于是有積分鏈路模型[14]：

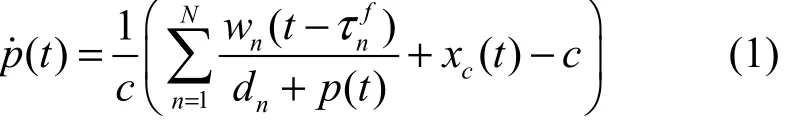
2.2 FAST模型和網絡

FAST TCP依據數據分組的排隊時延 pn(t -τ)來設置擁塞窗口，它的發送速率是通過擁塞窗口機制來調整的，每個發送源根據下式的離散時間更新窗口大小[15]：

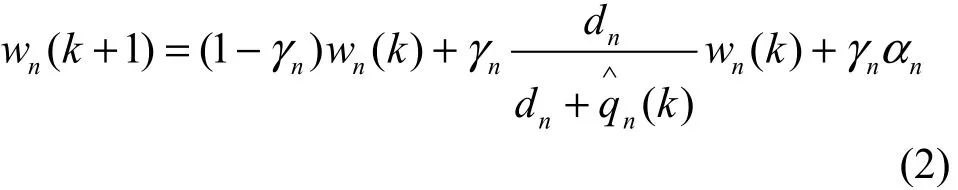
其中，αn∈Z+，αi是數據分組中的度量常數。γn為步長大小，是協議參數。窗口大小在每一個RTT之后執行更新一次。排隊時延 qn(k)是由數據發送端

∧估計出的，第 k次的估計表示為 qn(k )。窗口算法是以RTT為基礎進行，而估計值是以數據分組經歷的時間為基礎估算的。

3 穩定分析

3.1 二階穩定分析

式(1)和式(2)的連續時間形式拉普拉斯變換為

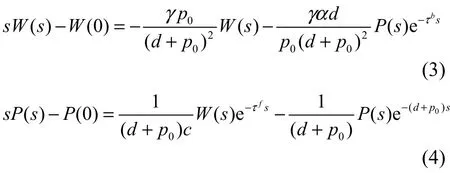
消去 ()Ps得：

運用padé二階近似得傳遞函數的特征多項式為

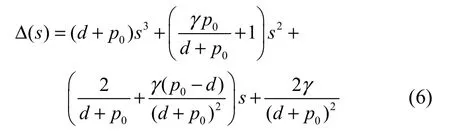
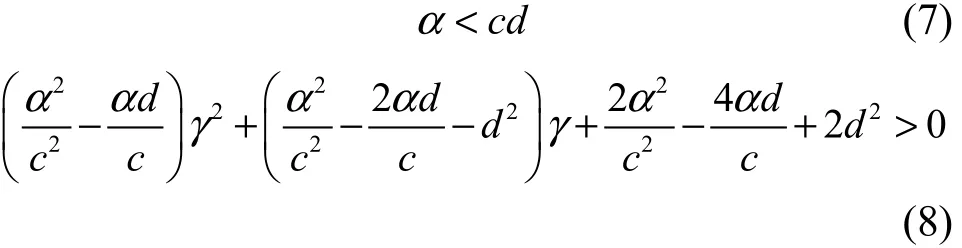
由以上2式，代入FAST TCP通常設置α、c和d的范圍，可得穩定范圍的上界約為1.55。為了得到工程應用上所許可的參數設置范圍，下面對系統進行一階近似來求系統穩定γ的設置范圍。

3.2 一階穩定性分析

瓶頸鏈路除了傳輸TCP流之外，也傳輸非窗口控制TCP流量，如UDP流量。令 xc(t)∈ [0 ,c]為非TCP流量大小，則TCP流量可以獲得的鏈路帶寬為c - xc(t)。根據來自于觀察經驗流量模型，窗口大小和鏈路緩存之間的關系可以表示為穩態鏈路模型[16]：

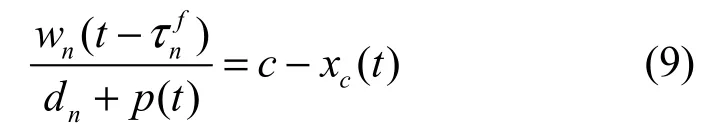
采用歐拉一階微分近似，式(2)的連續時間形式的拉普拉斯變換式為[17]

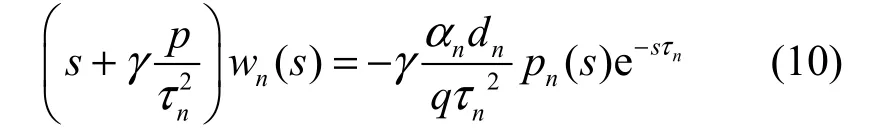
多個數據源共享一條瓶頸鏈路的窗口擁塞控制系統開環傳遞函數為

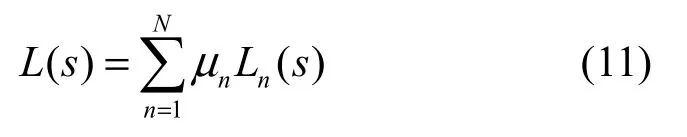
聯立式(10)和式(9)的拉普拉斯變換式可以建立基于穩態鏈路模型的一個負反饋系統，開環傳遞函數具有式(11)的形式，其中這里

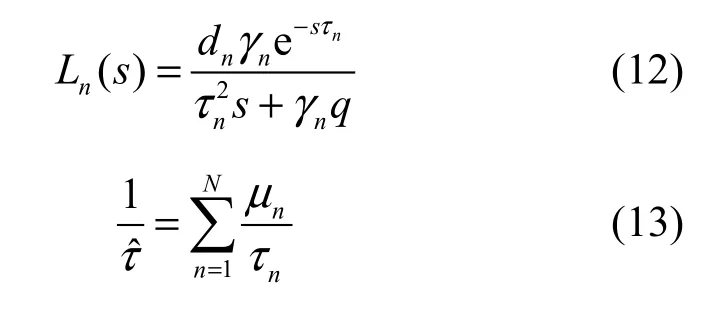
由此得到穩態鏈路的開環傳遞函數：

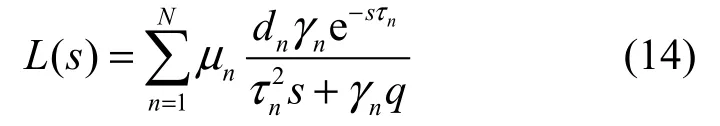
當 q → 0 時，每一項 Ln(s)都會增大，整個環路的傳遞函數的模會增大，系統的穩定性會下降，所以集中討論 q → 0 的情況。這時穩態鏈路的開環傳遞函數式(14)變為

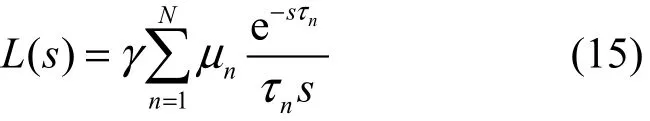
以下利用式(15)對系統穩定性進行分析。

3.2.1 1個FAST流在瓶頸鏈路上傳輸的情況

當N=1時，只有1個數據流，則1μ=，式(15)變為

在頻域內考察式(16)系統的穩定性，以jω代替s，繪制ω由0→∞奈奎斯特曲線。根據奈奎斯特穩定性判據，如果曲線自下而上順時針穿越區間( ,1)-∞- 的次數為0，則系統是穩定的。式(16)系統的頻率特性為

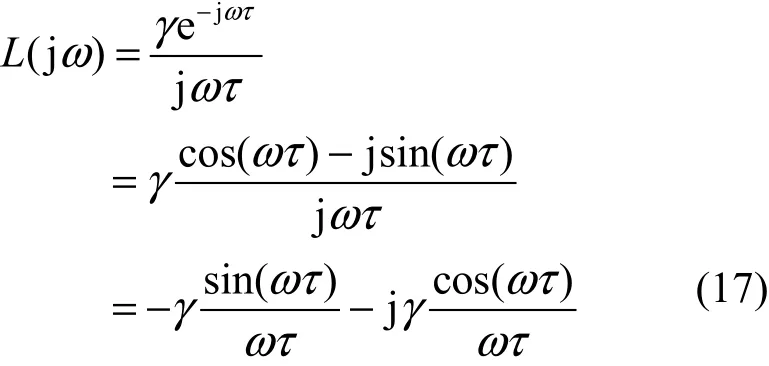
3.2.2 2個FAST流在瓶頸鏈路上傳輸的情況

設2個FAST流的往返時延有關系式τ2=ητ1，其中，η表示2個數據流往返時延差別系數，取值范圍為(1,+ ∞ )。式(15)變為

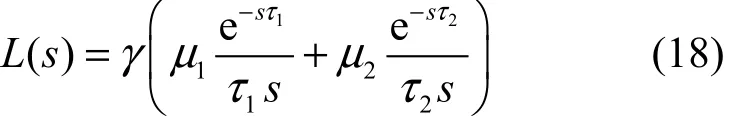
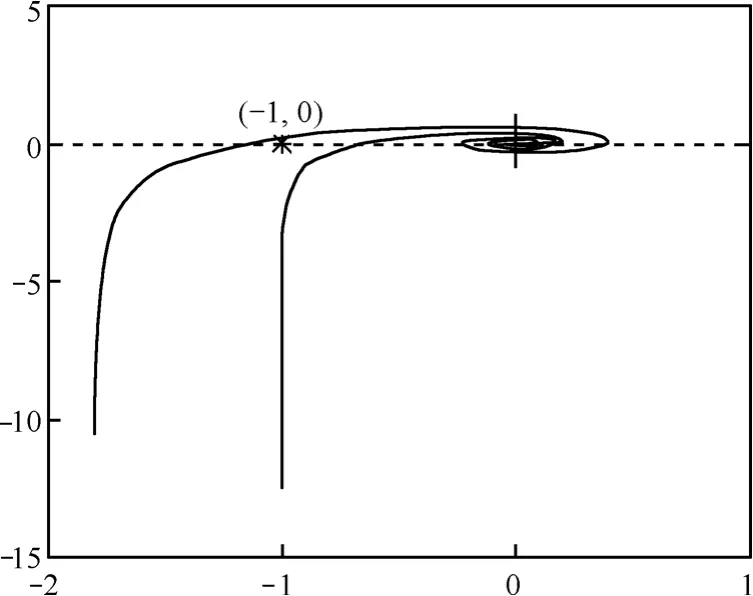
圖2 時系統的Nyquist曲線

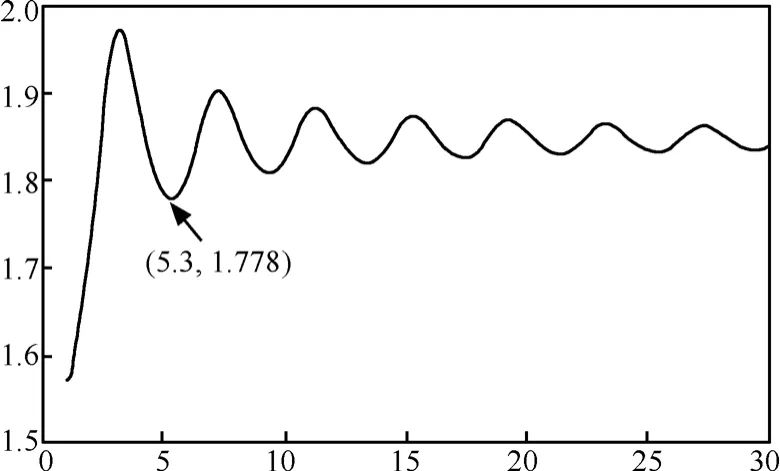
圖3 2個FAST流不同RTT情況下γ的穩定邊界

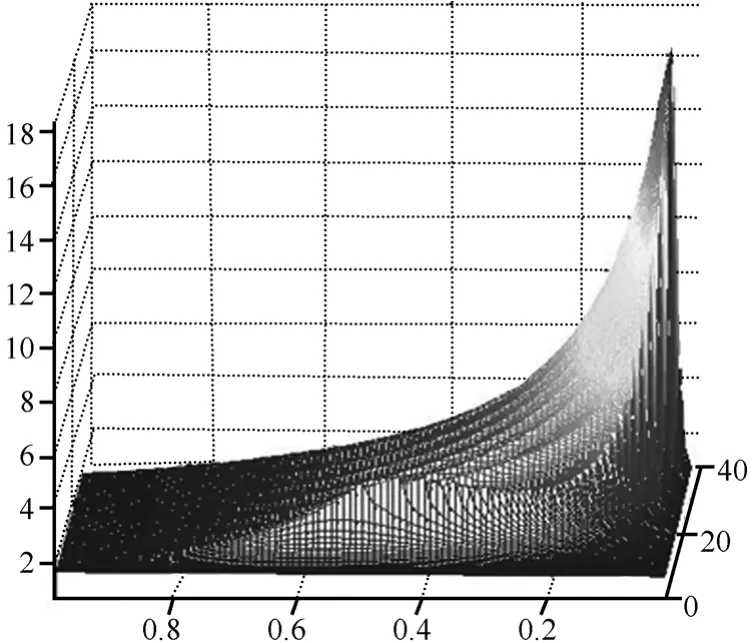
圖4 當η和μ變化時，γ使系統穩定的取值

3.2.3 N=∞個FAST流在瓶頸鏈路上傳輸的情況

在實際的網絡中，鏈路上有很多數據流同時傳輸。求出這種情況下穩定邊界條件的統計平均是有意義的。考慮很多個數據流的RTT呈均勻分布的情況，即令其中τ0為所有數據流中RTT最小值，τ為最大值，其最大可以為無窮大。

這時式(15)穩定條件可以表示為：在條件

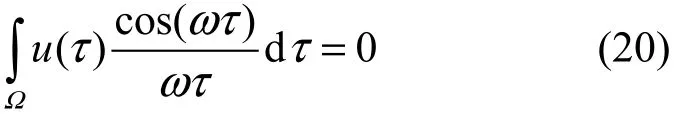
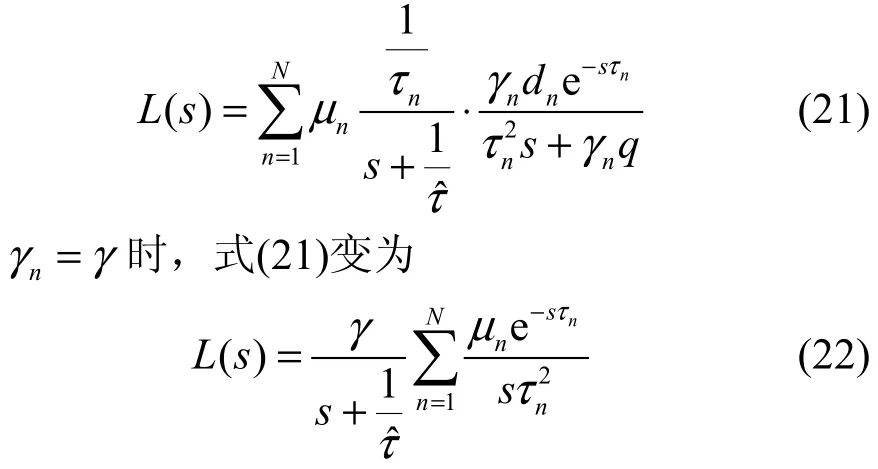
定理 如果

在式(18)描述的系統中，如果取η在區間(1,)+∞變化，1μ在(0,1)區間變化，可求出γ的穩定邊界如三維圖4所示。圖中的曲面是γ值的穩定邊界，γ取值在曲面上方時，系統不穩定，γ取值在曲面下方時，系統是穩定的。觀察γ的極小值點，可以看出1μ趨于0或者趨于1時，這時實際上退化到了1個FAST流傳輸的情況，γ的穩定邊界最小，1μ在0和1之間γ的穩定邊界都較大。這就是說，2個FAST流傳輸時γ的穩定邊界要大于1個FAST流傳輸的情況。

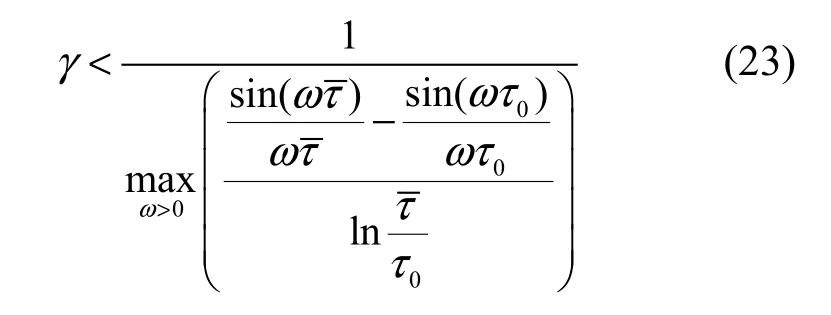
則在式(20)條件下，式(22)所確定的系統穩定。

證明設 H (ω)為復平面過點 - 1 + j0，斜率為的直線以下的半個平面如圖 5所示，如果Nyquist曲線在這個平面以下，則系統是穩定的。這個平面可以表示為

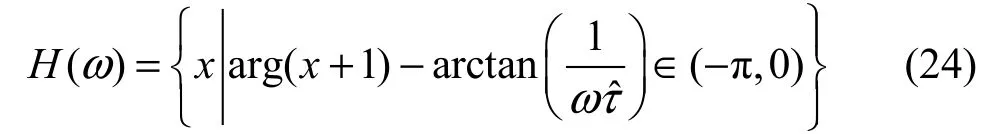
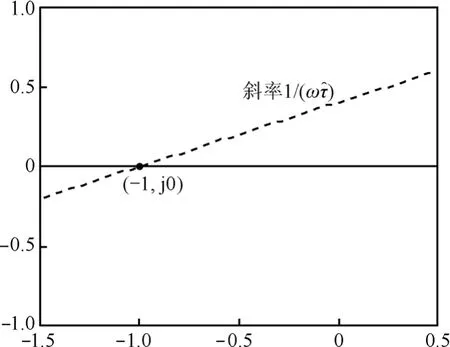
圖5 過點，斜率為的直線以下的半個平面

如果式(22)所確定的 L (s)滿足 L (jω)∈ H(ω)，則系統是穩定的。

L(jω)∈ H(ω)等價于

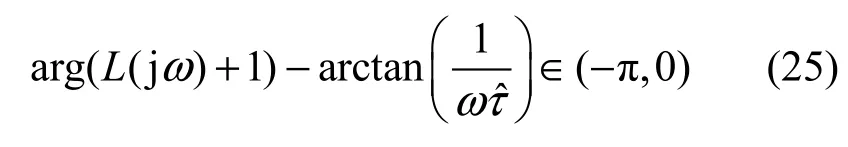
令s=jω，將式(22)代入式(25)，并考慮到

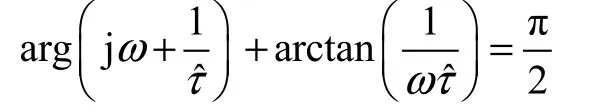
即當

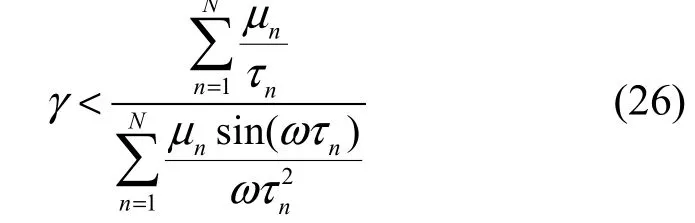
時，有 L (jω)∈ H(ω)。

當有無窮多個數據源N→∞時，式(26)變為

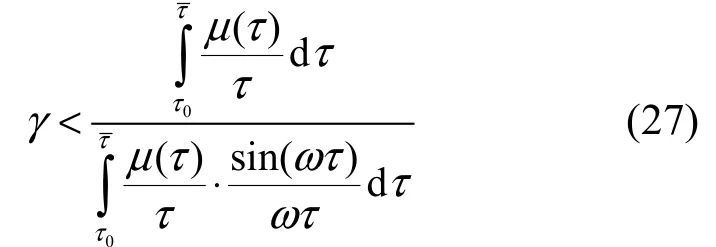
令θωτ=，由于有式(20)的條件，并假定總體上所有數據流的往返時延RTT服從均勻分布：

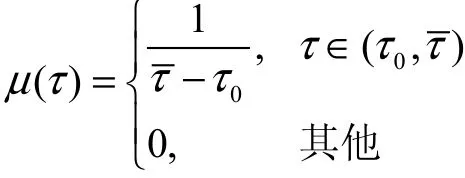
可得

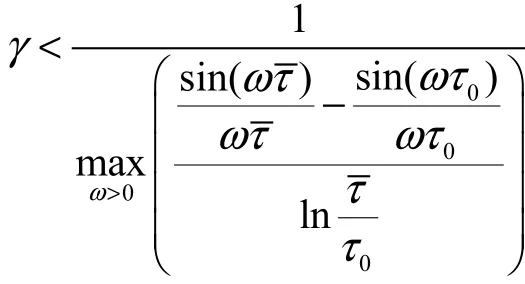
因為 L (jω)∈ H(ω)，根據Nyquist準則系統收斂，定理得證。

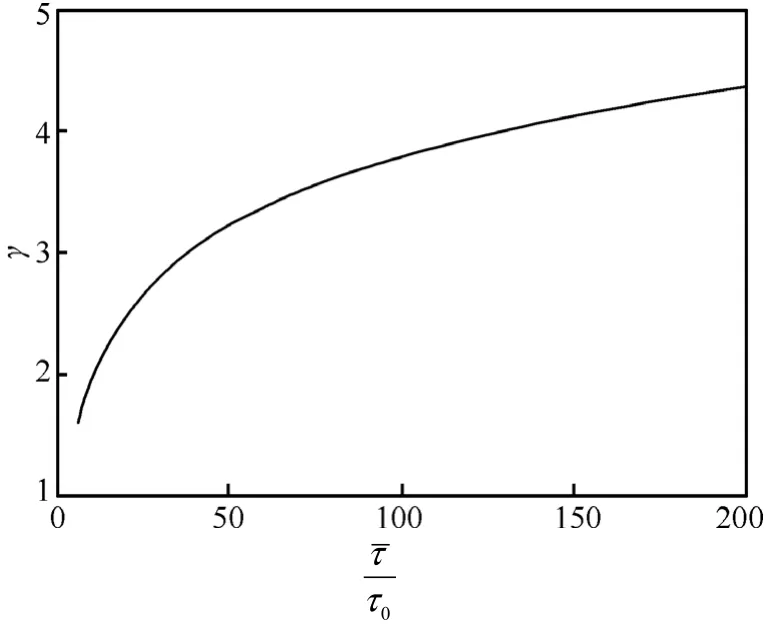
圖6 定理中不等式(23)所確定的γ的曲線

4 仿真

FAST的ns2仿真軟件在網站[18]上可以下載，設計實驗仿真場景來驗證參數γ對FAST 數據流傳輸穩定性的影響。多條FAST TCP數據流在一條容量為40Mbit/s的瓶頸鏈路上進行數據傳輸如圖1所示，傳輸的數據分組大小為 1 000byte，傳輸延時d= 2 0ms ，瓶頸鏈路的傳播時延為 4 ms，α=50packet。在1～500之間隨機選擇FAST數據流的個數進行傳輸，傳播時延在400～700ms之間均勻分布。研究γ穩定界限的最小上界，發現當設置 γ=1.55，γ=1.63或γ=1.75時，排隊隊列的變化如圖7(a)，圖7(b)和圖7(c)所示。圖7(a)表明當γ=1.55時，排隊隊列依然穩定，圖7(b)表明當γ=1.63時，排隊隊列開始出現波動，而圖7(c)表明當γ=1.75時，排隊隊列的波動很大了。這說明得出的參數γ的設置選擇范圍與實驗結果非常吻合。

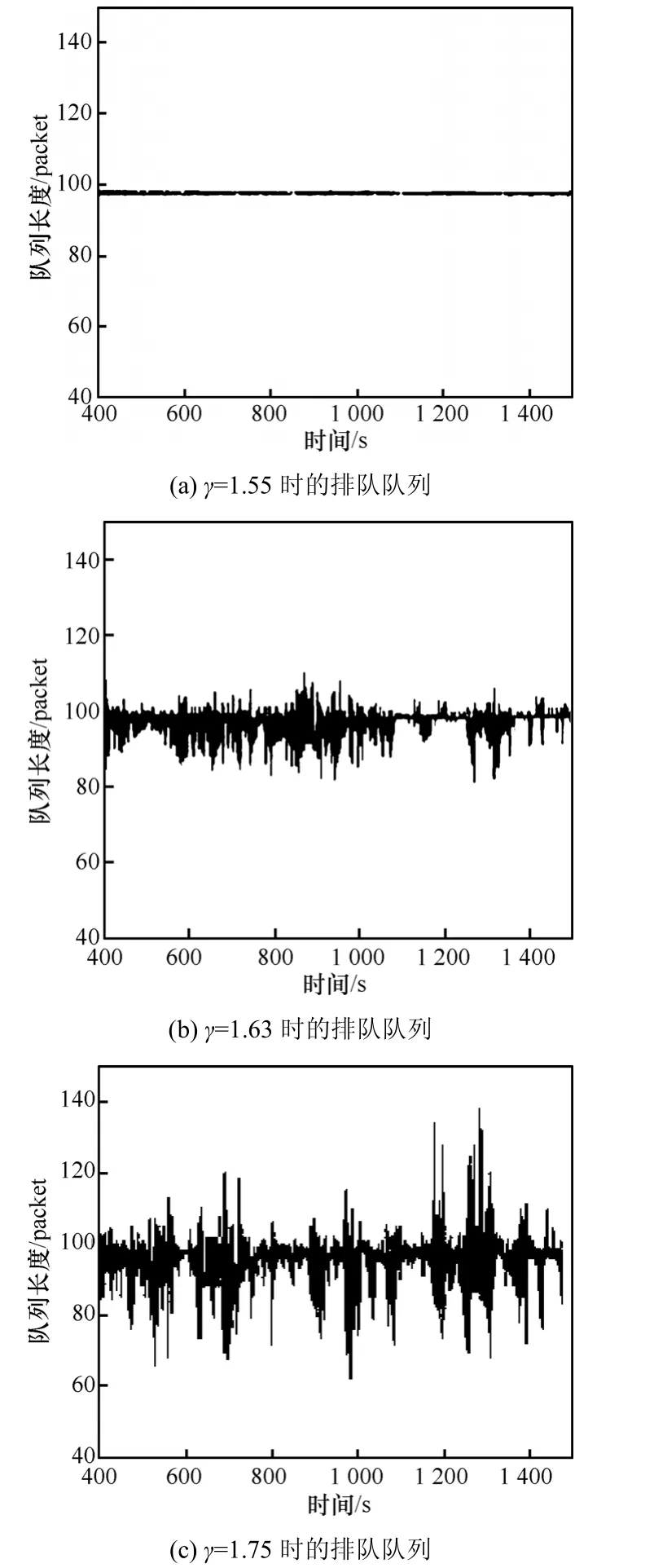
圖7 不同γ時的排隊隊列

5 結束語

本文根據穩態鏈路模型和積分鏈路模型對FAST TCP算法在復頻域建立了負反饋控制系統，深入地分析了在一條瓶頸鏈路上FAST流的傳輸情況。對系統傳遞函數進行了二階定性穩定分析，對1個FAST流、2個以及無窮多個數據源的情況下參數γ穩定邊界條件進行了分析，在1個數據流時，γ= 1 . 57。隨著傳輸的數據流的增多，參數γ的穩定邊界增大，系統穩定將趨于寬松，穩定取值將大大高于1.57，接著ns2仿真證實了所得結論。所得結論以控制理論作為依據，仿真結果與本文的理論研究符合很好。本文的研究成果有助于FAST TCP的實際應用，使得參數γ的設置選擇范圍有了明確的理論指導方針。在將來大規模地實際應用 FAST TCP情況下，對采用本文建議的參數γ的效果可以做進一步研究。

[1] BELHAJ S. VFAST TCP∶ an improvement of FAST TCP[A]. Proc Tenth International Conference on Computer Modeling and Simulation[C]. 2008.88-93.

[2] CHEN M, FAN X. Normalized queueing delay∶ congestion control jointly utilizing delay and marking[J]. IEEE/ACM Transactions on Networking, 2009,17(2)∶618-631.

[3] ZHANG H, PENG L, FAN B, et al. Stability of FAST TCP in single-link multi-source network[A]. Proc 2009 World Congress on Computer Science and Information Engineering[C]. 2009. 369-373.

[4] BAIOCCHI A, VACIRCA F. TCP fluid modeling with a variable capacity bottleneck link[A]. Proc IEEE INFOCOM [C]. 2007. 1046-1054.

[5] TAN L, ZHANG W, YUAN C. On parameter tuning for FAST TCP[J].IEEE Commun Letters, 2007, 11(5)∶ 458-460.

[6] WANG J, WEI D X, LOW S H. Modeling and stability of FAST TCP[A]. INFOCOM 2005.24th Annual Joint Conference of the IEEE Computer and Communications Societies[C]. 2005.938-948.

[7] JACOBSSON K, HJALMARSSON H, MOLLER N. ACK-clock dynamics in network congestion control—an inner feedback loop with implications on i nelastic flow impact[A]. Proceedings of IEEE Conference on Decision and Control[C]. San Diego, USA, 2006.1882-1887.

[8] JACOBSSON K, ANDREW L L H, TANG A, et al. ACK-clocking dynamics∶ modeling the interaction between windows and the net-work[A]. Proc IEEE Infocom[C]. 2008. 2146-2151.

[9] WEI D, JIN C, LOW S H, et al. FAST TCP∶ motivation, architecture,algorithms, performance[J]. IEEE/ACM Trans Networking, 2006,14(6)∶ 1246-1259.

[10] ZHAO F, ZHOU J, LU N. Stability analysis of FAST TCP based on lyapunov function[A]. Proc 7th Word Congress on Intelligent Control and Automation[C]. 2008.2136-2140.

[11] WANG J, TANG A, LOW S H. Local stability of FAST TCP[A].Proceedings of IEEE Conference on Decision and Control[C].2004.1023-1028.

[12] KOO K, CHOI J, LEE J S. Parameter conditions for global stability of FAST TCP[J]. IEEE Communications Letters, 2008,12(2)∶155-157.

[13] CHOI Y J, KO J W, YUN S W, et al. Improved global stability conditions of the tuning parameter in FAST TCP[J]. IEEE Communications Letters, 2009, 13(3)∶ 202-204.

[14] JACOBSSON K, ANDREW L, TANG A, et al. An improved link model for window flow control and its application to FAST TCP[J].IEEE Transactions on Automatic Control, 2009, 54(3)∶ 551-564.

[15] WEI D. Microscopic Behavior of Internet Congestion Control[D]. Pasadena, California, USA∶ California Institute of Technology, 2007. 36-37.

[16] TANG A, ANDREW L L H, JACOBSSON K, et al. Window flow control∶ macroscopic properties from microscopic factors[A]. Proc IEEE INFOCOM[C].2008.91-95.

[17] TANG A, JACOBSSON K, ANDREW L L H, et al. An accurate link model and its application to stability analysis of FAST TCP[A]. Proc IEEE INFOCOM[C]. 2007. 161-169.

[18] CUI T, ANDREW L. FAST TCP simulator module for ns-2, version 1.1[EB/OL]. http∶//www.cubinlab.ee.mu.oz.au/ns2fasttcp, 2009.