基于信號子空間的ESPRIT-Like算法在相干DOA估計中的應用
張洪順,許云林,湛江書
(1. 重慶通信學院 無線電管理教研室,重慶 400035;2. 重慶大學 資源與環境科學學院,重慶 400044)
1 引言
相干信號環境在現實中比較常見,如多徑效應或是在軍事通信中敵方有意實施干擾等情況,由于相干信號的影響,使陣列的空間協方差矩陣產生秩損失,從而使一些超分辨子空間類算法如多重信號分類[1](MUSIC, multiple signal classification)和利用旋轉不變技術進行信號參數估計[2](ESPRIT, estimation of signal parameter via rotational inviance techniques)在相干環境中失去效用,相干信號的 DOA(direction of arrival)估計是空間譜估計亟需解決的一個實際問題。目前相干信號預處理方法包括:空間平滑類算法、矩陣重構算法和非降維處理算法[3],但是這些算法都是以MUSIC作為DOA估計處理技術,由于MUSIC需要進行譜峰搜索,從而造成算法的運算量較大,且估計的穩健性不好。文獻[4]提出了一種在相干環境下的ESPRIT-Like DOA估計算法,作者通過計算機仿真分析,驗證了該算法的估計精度及解相關性能較空間平滑類算法及求根類算法都有明顯改善,且算法運算量較低。
本文在相干環境中信號子空間維數討論的基礎上,提出了2種尋找包含所有信號信息數據矢量的方法,然后利用所得數據矢量重構得到一個Toeplitz矩陣,對其進行奇異值分解即可得到信號子空間與噪聲子空間,最后利用ESPRIT方法進行DOA估計,即可得到所需結果。其中,本文第 2種數據矢量構造算法與文獻[4]中的方法殊途同歸。
2 窄帶信道數學模型
假設空間存在P個遠場窄帶信號,包括M個信源經多徑角度擴展得到的前L徑相干信號(令各信源的最大徑數分別為 l1,l2,…,lM)和后(P - L )個非相干信號,設信源統計獨立;又設接收陣列為均勻線陣,包含N( N ≥ P+1且N為奇數)個相同的全向陣元,陣元間距滿足“半波長條件”即d≤λ2(λ為信號波長),如圖1所示;信號DOA方向分別為θi( i = 1,… ,P ) ,假設空間噪聲為理想的高斯白噪聲,信號 si( t)(i = 1 , … ,P ) 與各陣元上的觀測噪聲統計獨立。
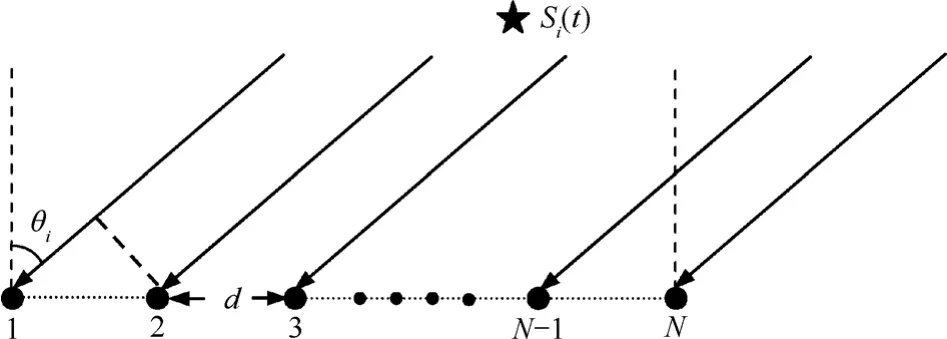
圖1 均勻線陣接收信號模型
以陣元1為參考陣元,則第k陣元上的觀測數據可表示為
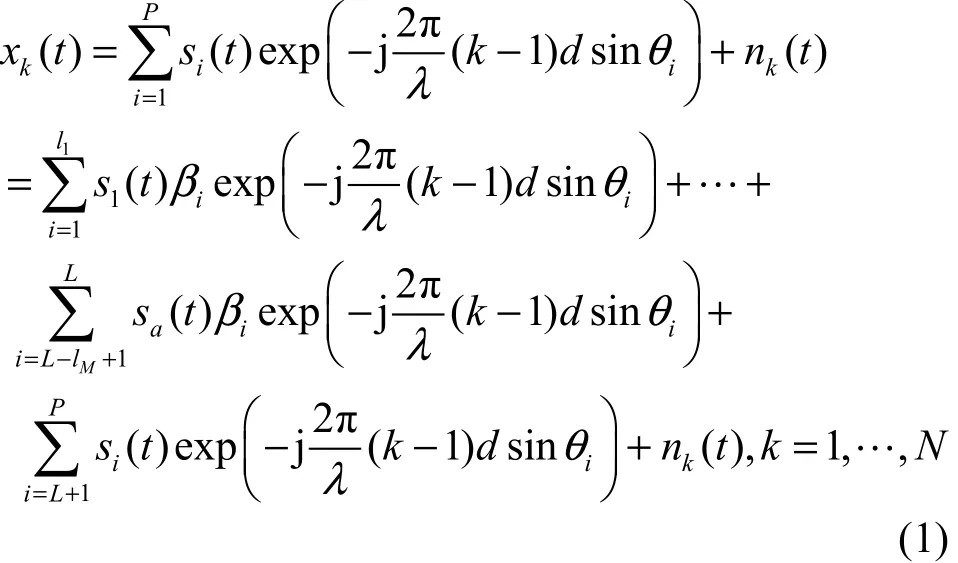
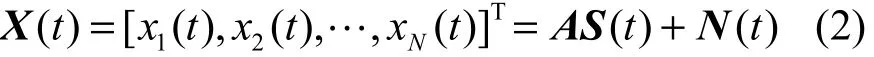
3 相干環境中信號子空間的維數
基于前面建立的理想高斯白噪聲條件下的信道模型,計算陣列接收協方差矩陣:
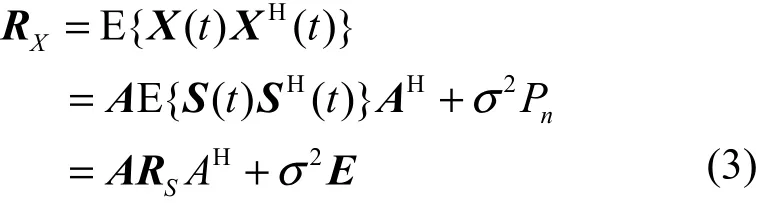
(?)H為復值共軛轉置,表示來波信號的協方差矩陣,σ2E表示噪聲的協方差矩陣,σ2為噪聲功率,E表示單位矩陣。由于假設陣列中理想陣元對信號來向是“敏感”的,即陣列對不同來向的信號具有不同的響應,由此可知,Vandermonde形式的陣列導向矩陣為列滿秩的,即rank(A) = P。令信號協方差矩陣 RS的秩為對陣列接收矩陣進行特征分解,對其特征值進行非增調排序可得:
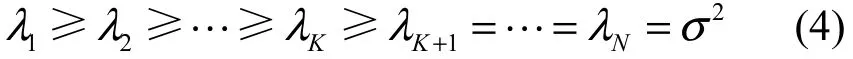
4 基于信號子空間的ESPRIT-Like算法
對相干信號的DOA估計包括解相干預處理與基于解相干基礎上的DOA估計2個部分,目前關于解相干的預處理基本有兩大類:一類是降維處理,可以分為基于空間平滑和基于矩陣重構2類算法;另一類是非降維處理,如頻域平滑算法、Toeplitz方法、虛擬陣列變換法等。其中,基于降維處理的算法更為常用。本文在預處理中運用基于矢量奇異值的矩陣重構,首先設法尋找包含所有信號信息的數據矢量,經矩陣重構實現解相干的目的,而后利用ESPRIT方法進行DOA估計的處理。
4.1 構建包含所有信號信息的矢量
矩陣重構的目標是要使重構后的矩陣可以估計出相干信號源的信號或噪聲子空間,因此,構建重構矩陣所需的數據矢量必須包含所有的信號信息。本文分析研究了2種構建包含所有信號信息數據矢量的方法,并在文章附錄部分給出了相關定理的證明過程。
1) 方法1。
由特征分解的定義X=RV ΛV,其中,V為特征矢量矩陣,Λ表示對角形式的特征值矩陣,將式(3)代入式X=RV ΛV可得:
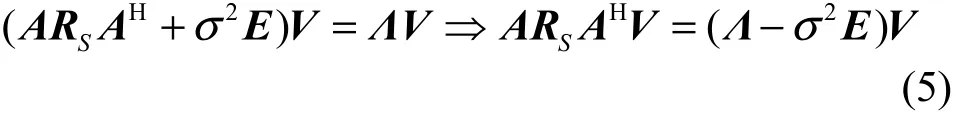
結合式(4)中的特征值分布情況可知,大特征值對應的信號特征矢量與矩陣 A RSAH的非零特征值對應的特征矢量是一致的。在此引出以下定理。
定理 1 假設 P ( P ≤ N-1)個窄帶遠場信號入射到N個陣元組成的陣列,則N×P陣列導向矩陣的秩為P,P×P信號協方差矩陣的秩為K(K≤P),又設噪聲為理想高斯白噪聲,N×N噪聲協方差矩陣為滿秩對角陣,則存在下列線形關系:
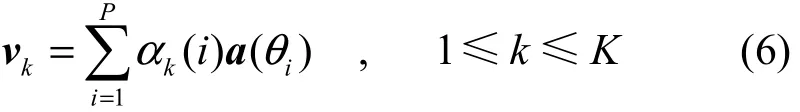
其中, vk(1 ≤ k ≤ K ) 表示信號特征矢量, αk( i ) 為線形組合因子,a ( θi)表示陣列接收第i個信號時的導向矢量(文獻[5]中給出了該定理的頻域表示形式,定理的詳細證明過程見本文附錄)。
定理1說明無論入射信號是否相干,對應大特征值的特征矢量是各信號導向矢量的一個線形組合,即包含了所有信號方向信息。為了提高后續DOA估計的精確性,本文在后續的仿真分析中對所有信號特征矢量進行求均,即有

2) 方法2。
在文獻[6]中提出了一種直接針對數據處理,得到一組無噪聲的快拍數據,同樣可以獲得一個包含所有信號信息的數據矢量:
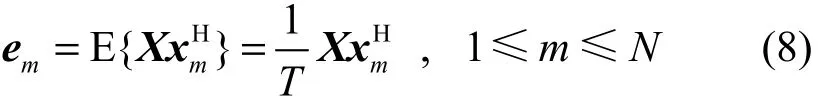
其中,T為取樣快拍數,xm表示1×T的任意一個參考陣元的接收數據矢量,X是N×T陣列接收數據矩陣,式中求數學期望也即對數據接收矩陣與參考陣元數據相乘后求時間平均。仔細分析可知,式(8)中的 em其實就是陣列接收數據協方差矩陣 RX的 第m(1 ≤ m ≤ N ) 行,在后續DOA估計的具體計算過程中可以對m進行求均,以提高DOA估計的精度[3]。
4.2 矩陣重構
為了利用上述2種數據矢量來實現解相干,本文利用獲得的2個數據矢量v和 em重構得到如下2個Toeplitz矩陣,其中 Y1表示由方法1中的v重構所得,Y2為由方法2中的無噪聲快拍數據矢量重構所得:
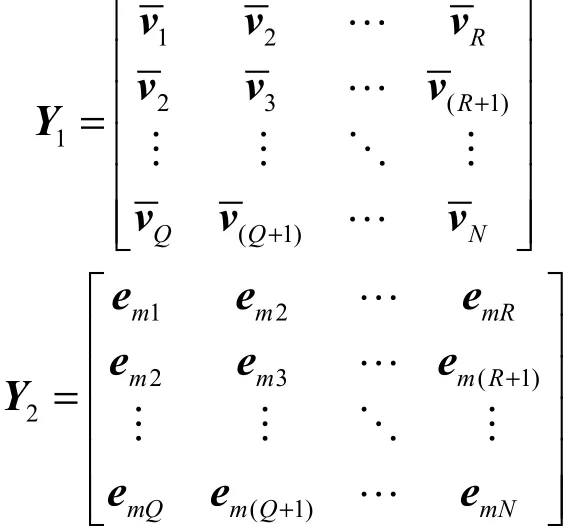

值得注意的是,式(9)中由無噪聲快拍數據矢量經矩陣重構所得矩陣 Y2′ 與文獻[4]中利用空間協方差矩陣直接重構得到的 Toeplitz矩陣 R ( m )在內容上是一致的,只是矩陣行的次序不同。分別對Y1′ 和 Y2′ 進 行奇異值分解有
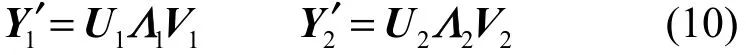
其中,Λ1、Λ2為由奇異值構成的p×p對角陣,U1、U2為左奇異矩陣, V1、 V2為右奇異矩陣。由文獻[6]中的證明過程可知, Y1′ 和 Y2′ 的大奇異值個數必為P,對應的左奇異矩陣 U1、 U2中的矢量組成的空間就是信號子空間,小奇異值對應的矢量組成的空間即噪聲子空間。
4.3 DOA估計
為了利用信號子空間對所有來波信號的方向信息進行精確估計,本文注重利用方法 1構造的Toeplitz陣Y1′進行DOA估計(方法2中通過 Y2′實現DOA估計的具體過程可參考文獻[4])。為了進一步說明如何結合 E SPRIT方法對矩陣 Y1′進行DOA估計處理,將式(9)中的 Toeplitz陣 Y1′以信號協方差矩陣的形式表示為

由4.2節的討論可知,對 Y1′進行奇異值分解可得P個大奇異值對應左奇異矩陣矢量組成的信號子空間和R-P個小奇異值對應矢量組成的噪聲子空間

對 US進行同樣分解,u 和 u 為 U 的第一行和最后一1RS行。由流型矩陣列向量張成信號子空間,即span{ ar( θ1) , … ,ar(θP)} = span{u1,u2, … ,uP},從而必存在非奇異矩陣T滿足進而可得
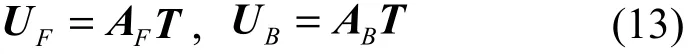
結合式(12)和式(13)有
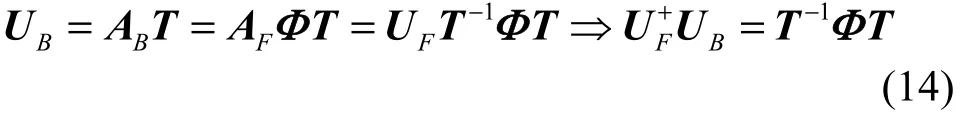
其中, ( ?)-1表示逆矩陣,(?)+表示矩陣的 Moore-Penrose廣義逆。令,對Ψ進行特征分解,其特征值即為進而估計出
5 數值仿真
在前面分析研究2種算法的基礎上,本文利用MATLAB進行了大量Monte-Carlo實驗。接收陣列為 11元等距均勻線陣,陣元間距為半波長,空間有3個完全相干信號,其載頻為900MHz,設采樣頻率為采樣點數為 N0=5 00個。
圖 2 中各信號來波方向分別為5°、10°、30°,SNR= 3 0 dB 時進行20次獨立試驗所得結果,圖中虛線為真實來波方向線,圖2(a)為利用算法1所得數據矢量進行估計,圖2(b)為采用算法2(即文獻[4]中的方法)獲取數據矢量進行的估計。從圖2觀察可知,2種算法均有較好的估計效果。
為了與空間平滑類算法進行比較,本文在SNR= 0 dB 條件下采用本文研究的2種算法和前向空間平滑算法[7,8],分別對3個完全相干信號(來波方向分別為5°、10°、30°)進行20次仿真試驗(見圖3),由圖3可以看出,在低信噪比情況下,前向空間平滑算法的譜峰分辨率明顯降低,甚至不可分辨(見圖3(c)),而本文2種算法的穩健性能較好,其中第1種算法有著更好的效果。
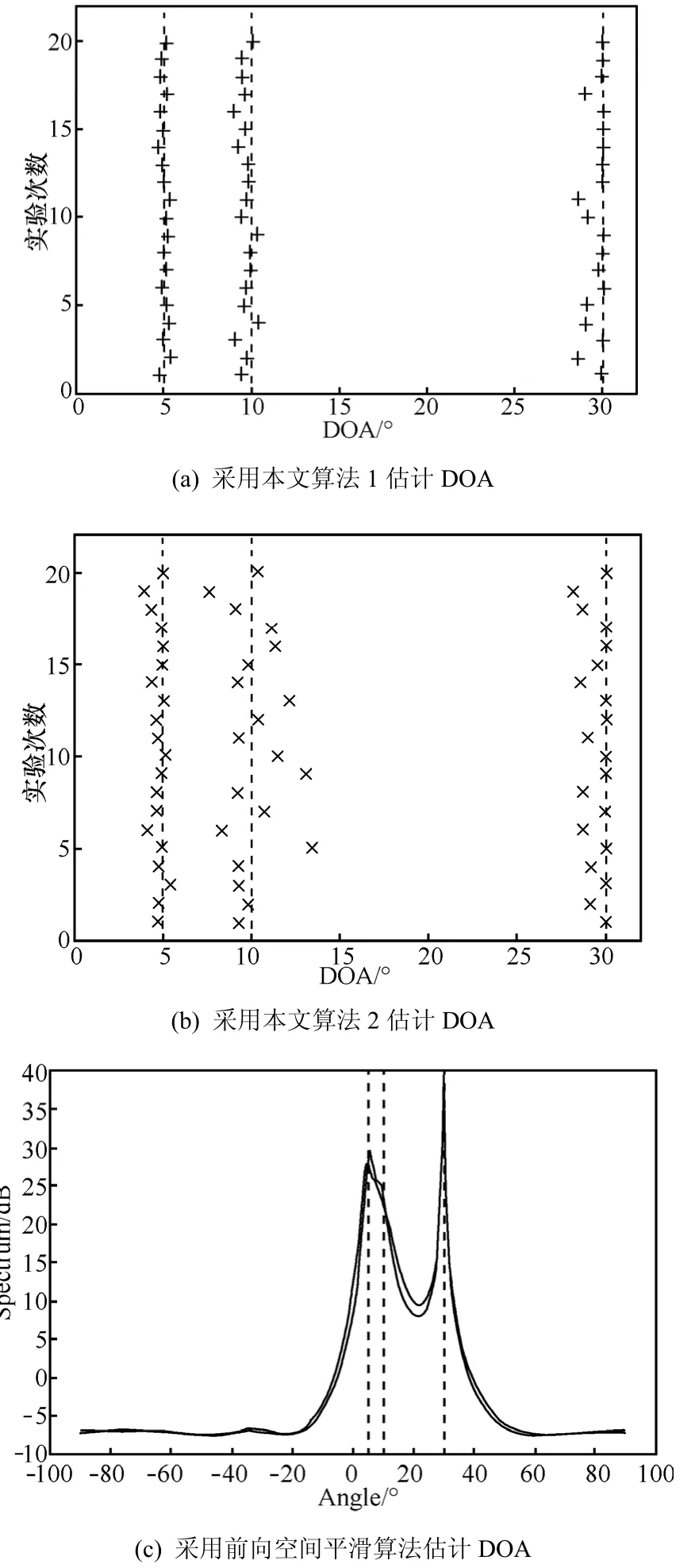
圖3 本文算法與前向空間平滑算法DOA估計的比較
圖 4為信號來波方向為 5-°、10°、5°時利用本文2種算法進行200次Monte-Carlo實驗所得3個方向的平均估計偏差圖,圖5為相同條件下3個方向的平均估計均方誤差(MSE)圖。
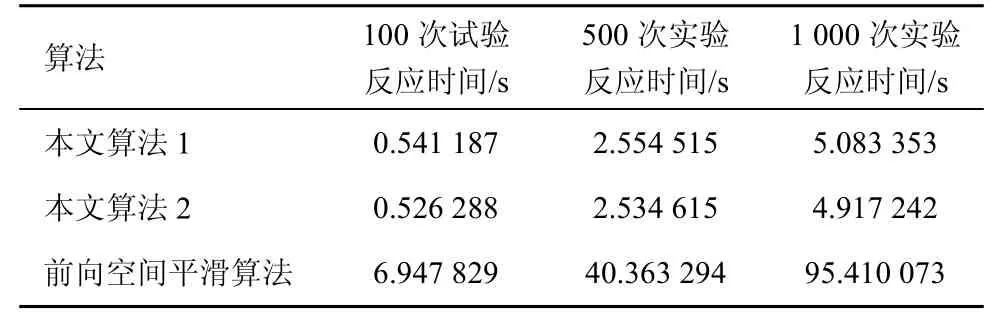
表1 2種方法估計反應時間比較
6 結束語
本文在討論相干信號環境特性的基礎上,提出了一種基于信號子空間利用ESPRIT進行處理的相干DOA估計算法,理論分析及計算機仿真表明,利用本文算法對相干信號進行DOA估計有著較好的解相干性能,其中方法1的算法性能更優。該算法的最大優點在于運算量低,且在低信噪比條件下仍有較好的效果。但是根據理論分析可知,與空間平滑類等解相干算法相同,該算法是以犧牲有效陣元數為代價的。另外,該算法在其他特殊陣列中的應用方面還有待進一步研究。
附錄 定理1的證明
為降低證明過程的復雜性,在此考慮最極端的情況,假設K=1(入射信號完全相干), 接收信號完全由某個源信號與一組復值衰落因子相乘所得,S (t ) = Bs1(t),其中,s1(t)表示唯一生成源信號, B = [ β1,β2,… ,βP]T為衰落系數向量,表示源信號 s1(t)第 i 徑復值衰落系數。此時理想高斯白噪聲條件下陣列接收信號的協方差矩陣為
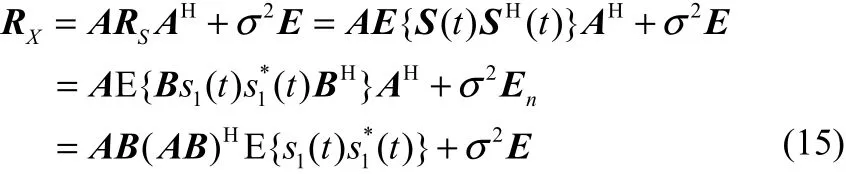
其中, ( ?)*表示復數共軛。對RX進行特征分解則有λ為唯一的大特征1值, v1表示該大特征值對應的 N × 1特征矢量,最后可以計算得到下式:
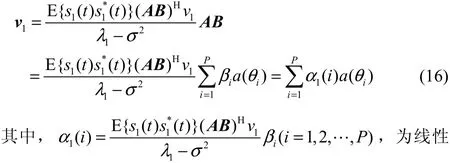
組合因子。在信號部分相干的情況下,可以同樣利用該方法進行證明。
[1] SCHMIDT R O. Multiple emitter location and signal parameter estimation[J]. IEEE Trans on AP, 1986,34(3)∶276-280.
[2] ROY R, KAILATH T. ESPRIT—estimation of signal parameters via rotational invariance techniques[J]. IEEE Trans ASSP,1989,37(7)∶984-995.
[3] WANG Y L, CHEN H. Spatial Spectrum Estimation Theory and Method [M]. Beijing∶Tsinghua University Press, 2004.
[4] HAN F M, ZHANG X D. An ESPRIT-like algorithm for coherent DOA estimation[J]. IEEE Antennas and Wireless Propagation,2005,4∶443-446.
[5] CADZOW J A, KIM Y S, SHIUE D C. General direction-of arrival estimation∶ a signal subspace approach[J]. IEEE Trans on AES, 1989,2S∶ 31-47.
[6] GAO S W, BAO Z. Data matrix decomposition for super-resolution reconstruction of spatial coherences source[J]. Communication Journal,1988, 9(1)∶4-13.
[7] SHAN T J, WAX M, KAILATH T. On spatial smoothing for estimation of coherent signals[J]. IEEE Trans on ASSP,1985,33(8)∶806-811.
[8] LI H S, HOU T, ZHU Z D, et al. Performance of DOA estimation for correlated sources by forward-backward spatial smoothing [J]. Journal of Harbin Institute of Technology, 2007,3∶416-419.

