改進恒Lyapunov指數譜混沌系統的同步方法與特性研究＊

李春彪 胡 文1)(江蘇經貿職業技術學院工程技術學院,南京 210007)2)(江蘇省食品安全工程技術研究開發中心電源與系統部,南京 210007)(南京航空航天大學信息科學與技術學院,南京210016)

Li Chun-Biao1)2)? Hu Wen3)

1)(Department of Engineering Technology,Jiangsu Institute of Econom ic and Trade Technology,Nanjing 210007,China)

2)(Department of Electric Source and System,Research and Development Center of Food Safety Engineering Technology of Jiangsu Province,Nanjing 210007,China)

3)(School of Infor mation Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

改進恒Lyapunov指數譜混沌系統的同步方法與特性研究＊

李春彪1)2)?胡 文3)
1)(江蘇經貿職業技術學院工程技術學院,南京 210007)
2)(江蘇省食品安全工程技術研究開發中心電源與系統部,南京 210007)
3)(南京航空航天大學信息科學與技術學院,南京210016)

(2009年5月6日收到;2009年6月9日收到修改稿)

改進恒Lyapunov指數譜混沌系統的特殊的分段線性結構及其全局線性調幅參數與倒相參數的存在性,賦予了其同步體系新的可實現性與可調節性.依據廣義同步的原理,構造合適的驅動系統與響應系統,可以實現恒Lyapunov指數譜混沌系統的廣義同步;改變響應系統的參數,可實現完全同步與廣義投影同步;改進恒Lyapunov指數譜混沌系統的全局線性調幅參數能對驅動與響應系統的狀態變量幅值實施同步升降控制,倒相參數能對某一特定狀態變量實施同步倒相控制.這種同步體系無需專門的控制器,結構簡單,易于實現.文章最后設計了同步體系的實現電路,實驗仿真結果證明了混沌同步方法的可行性,也驗證了恒指數譜混沌系統特殊參數對同步體系狀態變量幅值與相位的調控作用.

改進恒Lyapunov指數譜混沌系統,同步,幅值控制,倒相控制

PACC:0545

1.引言

混沌信號應用于雷達與通信系統已經成為極為活躍的研究領域[1—4].要將混沌系統應用于雷達與通信等實際工程中,往往需要給出正確可行的電路實現方案與同步方案[5—15].正是基于這一原因,多年來,人們對混沌同步的研究不斷深入,提出了許多有效而可行的混沌控制與同步方法[5—12],如驅動-響應同步法[5,6]、線性反饋法[7—11]、非線性反饋法[11]、自適應控制同步法[12,16]、非線性狀態觀測器方法[17]等.1999年,Mainieri和Rehacek[18]在部分線性混沌系統中觀察到一種稱為投影同步的新的同步現象,該同步使得在一定條件下耦合的主從系統的狀態變量相位鎖定,振幅恒比例且可調.此后,投影同步便引起了人們的廣泛關注[13,14,19—28].而最近出現的廣義投影同步方法及其應用研究[13,14,23—28],將投影同步與廣義同步聯系了起來,通過比例因子的調節作用實現任意比例于驅動混沌系統輸出的混沌信號.實現廣義投影同步通常采用單向線性耦合方法[22]、驅動響應方法[23—25]、主動控制方法[13,26,27]和自適應投影同步方法[28]等.

最近,Li等[15]提出一種新的具有恒Lyapunov指數譜的類Colpitts混沌吸引子,通過參數剝離,繼而得到一種具有雙參數恒Lyapunov指數譜特性的改進系統[29],添加線性項與常數項又推廣得到一族恒指數譜混沌系統[30].文獻[31]對改進系統的廣義投影同步進行了研究,得到了該系統的同結構與異結構廣義投影同步控制器,設計了同步體系的實現電路,指出了其廣義投影同步體系中存在的內外兩個幅值調節因子[31].實際上,恒Lyapunov指數譜混沌系統特殊的分段線性結構及其特殊參數也賦予了系統同步新的可實現性與可調節性.本文以改進恒Lyapunov指數譜系統[29]為研究對象,依據廣義同步原理,構建新的同步體系;在此基礎上,進一步實現完全同步與廣義投影同步;同時揭示恒指數譜混沌系統的同步特性,指出其同步體系中所存在的特殊的幅值與相位可控性.由于混沌電路實驗是研究混沌系統動力學特性和驗證混沌控制與同步方法有效性的重要手段,同時混沌電路及其同步體系的實現電路也是混沌在電子信息領域應用的一個重要基礎與前提,因此,本文在繼數值仿真之后,設計了同步體系中驅動與響應系統的實驗電路;通過參數的設置與調整,可以實現不同的同步方法;借助于電路仿真PSpice軟件平臺,驗證了同步方法的正確性,也驗證了恒指數譜混沌系統之同步體系幅值與相位的特殊可調節性.恒Lyapunov指數譜混沌系統自身的優勢與特征轉移到相應的同步體系中,增加了其同步體系的幅度與相位控制自由度,提升了恒指數譜混沌系統的工程應用價值.

2.廣義同步方法設計

2.1.廣義同步的基本原理

設有單向耦合(驅動的混沌動力學參數不依賴于響應系統的參數)的混沌系統,驅動系統和響應系統的行為可以表示為

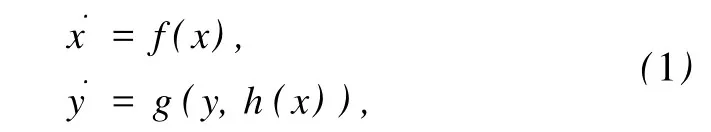
其中,x∈Rn,y∈Rm,h:Rn→Rm,˙x=f(x)為驅動系統,˙y=g(y,h(x))為響應系統.

定義[32]設存在變換H:Rn→Rm,一個函數流形M以及一個子集B=Bx× By?Rn×Rm,且滿足M?B,當且僅當所有初始條件(x0,y0)?B的響應系統軌道都隨時間趨于無窮而趨于M,即當t→∞時,響應系統的軌道滿足y= H(x),則稱(1)式的兩個系統廣義同步.當n=m時,則廣義同步回到一般意義上的完全同步,即y= H(x)=x.

在廣義同步的兩個子系統中,如果驅動系統能分解為線性部分與非線性部分x˙=Ax+Φ(x),其中A是n×n系數矩陣,Ax是f(x)的線性部分, Φ(x):Rn→Rn是非線性部分.可以讓函數Φ(x)作為驅動信號去作用于響應系統.考慮單向傳輸的兩個系統同步,構造相應的驅動與響應系統

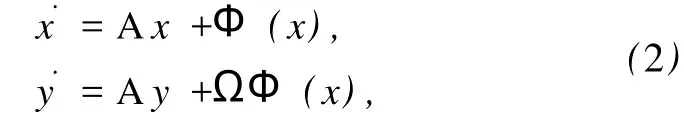
這里,上式代表驅動系統,下式代表響應系統.

引理[33]如果Ω是A的對易矩陣,即滿足AΩ =ΩA,則當t→∞,且A的特征值實部全部為負數時,響應系統的軌道與驅動系統的軌道將實現廣義同步,即y=H(x)=Ωx.

證明[33]令系統誤差為Δ=y-Ωx,對誤差求導并代入上述系統函數,有

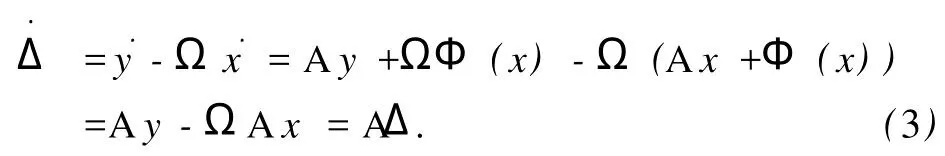
當誤差系統(3)中矩陣A的所有特征值實部全為負數時,則Δ→0,誤差系統漸近穩定.因此,只要構造出滿足上述條件的矩陣A和Ω,則可以使驅動系統和響應系統滿足t→∞時,y→Ωx=H(x),從而實現廣義同步.

2.2.廣義同步方法設計

改進恒Lyapunov指數譜混沌系統的數學模型為[29]

這里,a,b,c,d為實常數,當參數取a=d=3,b= 0.4,c=1.62時,系統狀態變量的演變呈現混沌特性.文獻[29]指出,d為全局線性調幅參數,d發生變化,系統輸出信號x,y,z的幅值也都隨著作線性變化;倒相參數a的極性的改變能夠對系統輸出的z信號實施倒相控制;系統(4)相對于上述兩個參數皆呈現恒定的Lyapunov指數譜.下面就基于廣義同步思想著手研究該系統的同步方法,在此基礎上,再對恒Lyapunov指數譜混沌系統的同步特性進行進一步的分析.

2.2.1.驅動系統的構造

針對改進恒Lyapunov指數譜混沌系統(4),構造驅動系統為

根據Routh-Hurwitz判據,當b>0時,要使得矩陣A的特征值實部全部為負,必須滿足以下關系:

此時,以系統(5)作為驅動系統,與響應系統相耦合,響應系統與驅動系統之間就能夠實現廣義同步.實際上,驅動系統就是原來的改進恒Lyapunov指數譜混沌系統(4),這一點是不變的,改變的只是形式而已.

2.2.2.響應系統的構造

根據引理,系統(5)相應的響應系統具有以下形式:

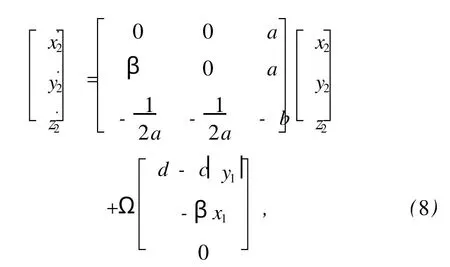
由(3)式可知,Δ˙=AΔ,在b>0,且0<β<2b時,Δ→0,誤差系統漸近穩定.當滿足Ω是A的對易矩陣時,構造的響應系統與驅動系統之間能夠實現廣義同步.

選擇不同的A的對易矩陣Ω可以構造多種不同的廣義同步系統,當選擇0)時,也有ΩA=AΩ成立,由方程(8),得到相應的響應系統為

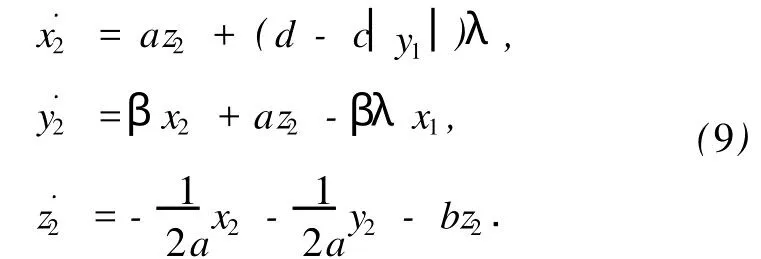
根據廣義同步引理,響應系統(9)的輸出狀態為

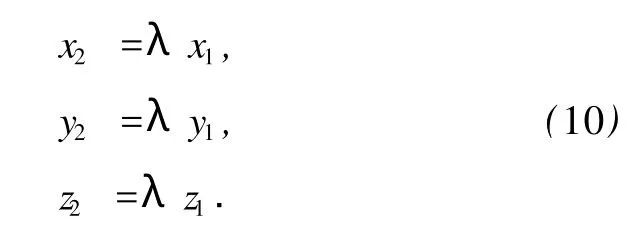
由(10)式可見,在Ω作如上選擇時,當響應系統與驅動系統之間實現廣義同步,響應系統的狀態變量是驅動系統的對應狀態變量的λ倍,響應系統不但跟蹤了驅動系統的狀態變量,選擇與調節λ還能夠實現對驅動系統的輸出信號進行衰減、放大甚至倒相衰減或者倒相放大.也就是說,基于廣義同步方法可以進一步實現完全同步與廣義投影同步.與廣義投影同步中的比例因子相比較,這里的λ反映的是響應系統與驅動系統之間的狀態變量的比例關系,而不是驅動系統與響應系統之間的比例關系,故也可稱為比例因子,但其實際含義與廣義投影同步中的比例因子不同[31],兩者存在倒數關系.與之相對應,后面誤差信號的定義也相應地改為響應系統輸出的狀態變量與驅動系統狀態變量之差.

3.完全同步與廣義投影同步及其同步特性分析

3.1.完全同步:λ=1

取β=0.5,當λ=1時,初始值不同的響應系統與驅動系統(不妨設初始值分別為(0,1,0)與(1,0,1))之間實現了完全同步.設響應系統與驅動系統之間狀態變量的誤差為e1=x2-x1,e2=y2-y1,e3=z2-z1,同步時的狀態變量相圖與同步誤差曲線如圖1所示.

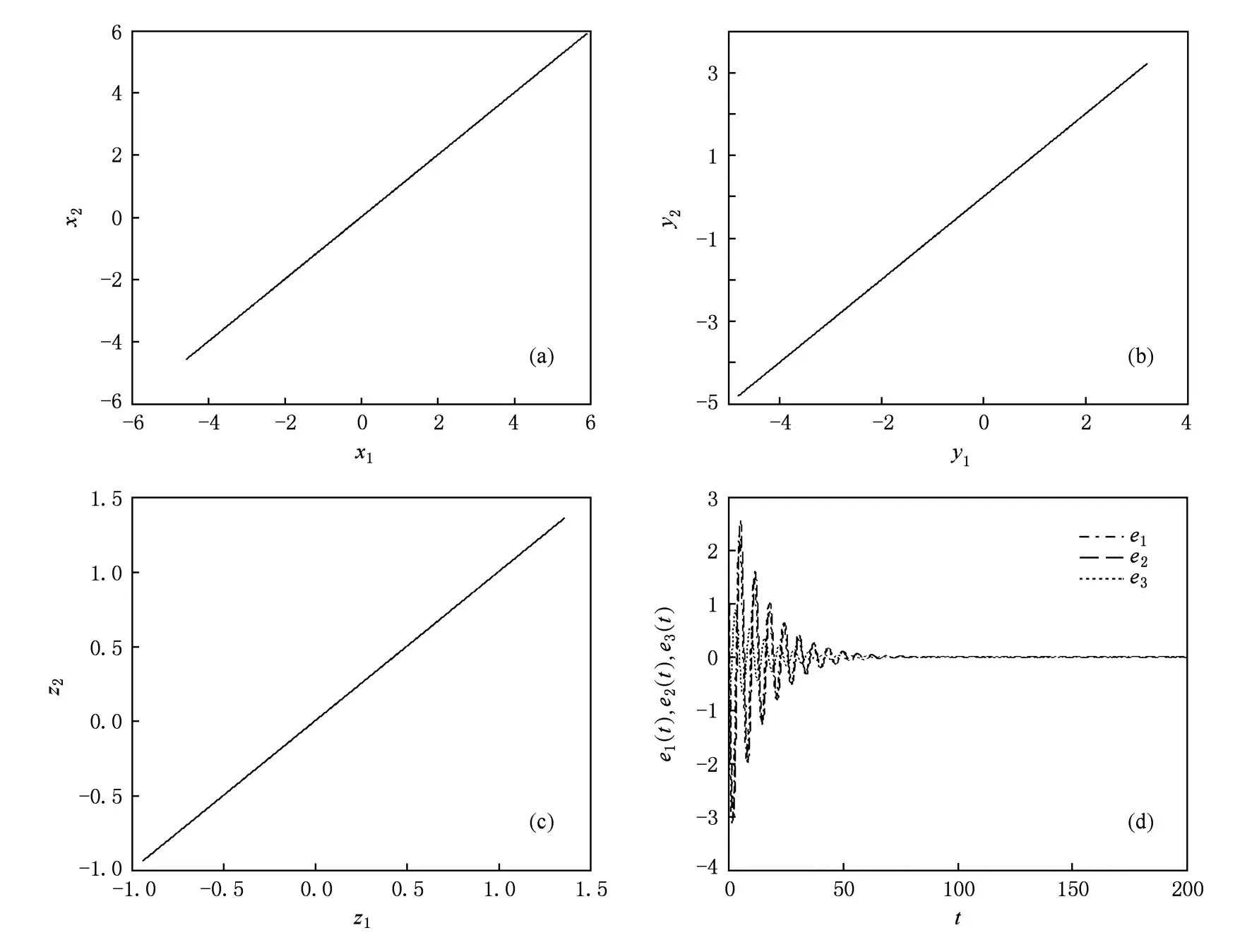
圖1 完全同步時的狀態變量相圖與同步誤差曲線 (a)x1-x2相圖;(b)y1-y2相圖;(c)z1-z2相圖;(d)e(t)-t同步誤差曲線

改進恒Lyapunov指數譜混沌系統的特性必然帶給其同步體系新的性能,系統(4)中存在的兩個特殊參數,即全局線性調幅參數d與倒相參數a對同步體系的狀態變量波形演變也具有特殊的調節與控制作用.對于單個混沌系統而言,全局線性調幅參數d能線性調整混沌系統的狀態變量演變幅值,使之上升或下降.采用文獻[29,30]的推理方法可知,同步體系中響應與驅動兩個子系統輸出的六個狀態變量演變幅值的線性調整,也同樣對應于常數項控制器d的尺度變化.如圖2所示,當同步體系中的d由3調整至6,在響應系統與驅動系統之間建立同步關系以后,響應系統輸出的混沌吸引子相比于d=3的情況得到了放大(見圖2(a),(d)),這種放大反映到混沌波形及其幅度上來也是一致的,由于d提高了1倍,狀態變量的演變幅度也相應地提高了1倍(見圖2(b),(e)與(c),(f)).可見,原來作用于獨立混沌系統的常數項控制器d,其功能也相應轉移到由響應與驅動兩個子系統復合而成的同步體系中來.在改進恒指數譜混沌系統的同步體系中,常數項d依然能對同步體系輸出的狀態變量演變幅值進行同步升降控制,常數項控制器d是同步體系的全局幅度調節器.

繼續考察倒相參數a在同步體系中的作用.文獻[30]指出,由于混沌系統具有初始值敏感性,而系統的初始值又是人為強制設定的,初始值是系統振蕩的起點,因此為了觀測到a的嚴格倒相作用,需要將系統初始值設定為(x0,y0,z0)(其中z0=0),或者在改變a的極性的同時,將系統初始值中z0的坐標也設定為原來的相反數-z0,否則倒相作用將由于初始值z0坐標的強扭作用而被遮蔽.同樣采用文獻[29,30]的推理方法,可以推斷,倒相參數a對于同步體系中驅動與響應兩個子系統的特定狀態變量也具有倒相控制作用.不妨將驅動系統的初始值坐標設定為(1,-1,0),響應系統的初始值坐標設定為(-1,1,0),改變倒相參數極性,使a=-3,響應與驅動兩個子系統之間同樣很快建立起了同步關系(見圖3(a)),而同步體系中響應系統輸出的混沌信號z2(t),相比于a=3的情況得到了嚴格的倒相控制(見圖3(b)).當然,驅動系統的相應混沌信號z1(t)也一樣被嚴格倒相,因為響應系統與驅動系統之間是完全同步的.保持驅動系統的初始值不變,將響應系統的初始值坐標設定為(-1,1,2)時,改變倒相參數使a=-3以后,響應系統輸出的z2(t)信號被倒相,但是由于初始值的強制作用,使得這個倒相作用受到遮蔽(見圖3(c)).當響應系統的初始值設定為(-1,1,2)時,在a改變極性以后,相應地將此初始值的z0坐標也作相反數設置,即設定為(-1,1,-2),這樣,同步體系中響應系統輸出的z2(t)信號的倒相作用將清晰地顯現出來(見圖3(d)).值得強調的是,同步體系的工作狀態受到驅動系統的初始值的影響很大,如果驅動系統設置不合適的初始值,有可能會導致驅動系統根本不振蕩,此時也就無所謂同步問題,而響應系統的初始值設定則相對比較自由,只是在觀測倒相參數的倒相控制作用時,需要初始值中的z0坐標隨倒相參數a的極性改變的同時設置為其相反數.

圖2 參數d實現幅度調節 (a)混沌吸引子在x-z的平面投影(d=3),(b)信號x2(t)(d=3), (c)信號幅值(d=3),(d)混沌吸引子在x-z的平面投影(d=6),(e)信號x2(t)(d=6),(f)信號幅值(d=6)

可見,改進恒Lyapunov指數譜混沌系統中存在的兩個特殊參數,賦予了其同步體系新的可控制性,全局線性調幅參數d對響應與驅動兩個子系統狀態變量的演變幅值實現線性增減控制,而伴以響應系統初始值的相應調整,倒相參數a可以對同步體系中兩個子系統的狀態變量z(t)實施同步倒相控制.這種由混沌系統的特殊性所帶來的幅度與相位可控性是其他混沌系統的同步體系所沒有的,同步體系的新的幅度與相位可控性,為恒指數譜混沌系統的工程應用提供了更大的應用空間.

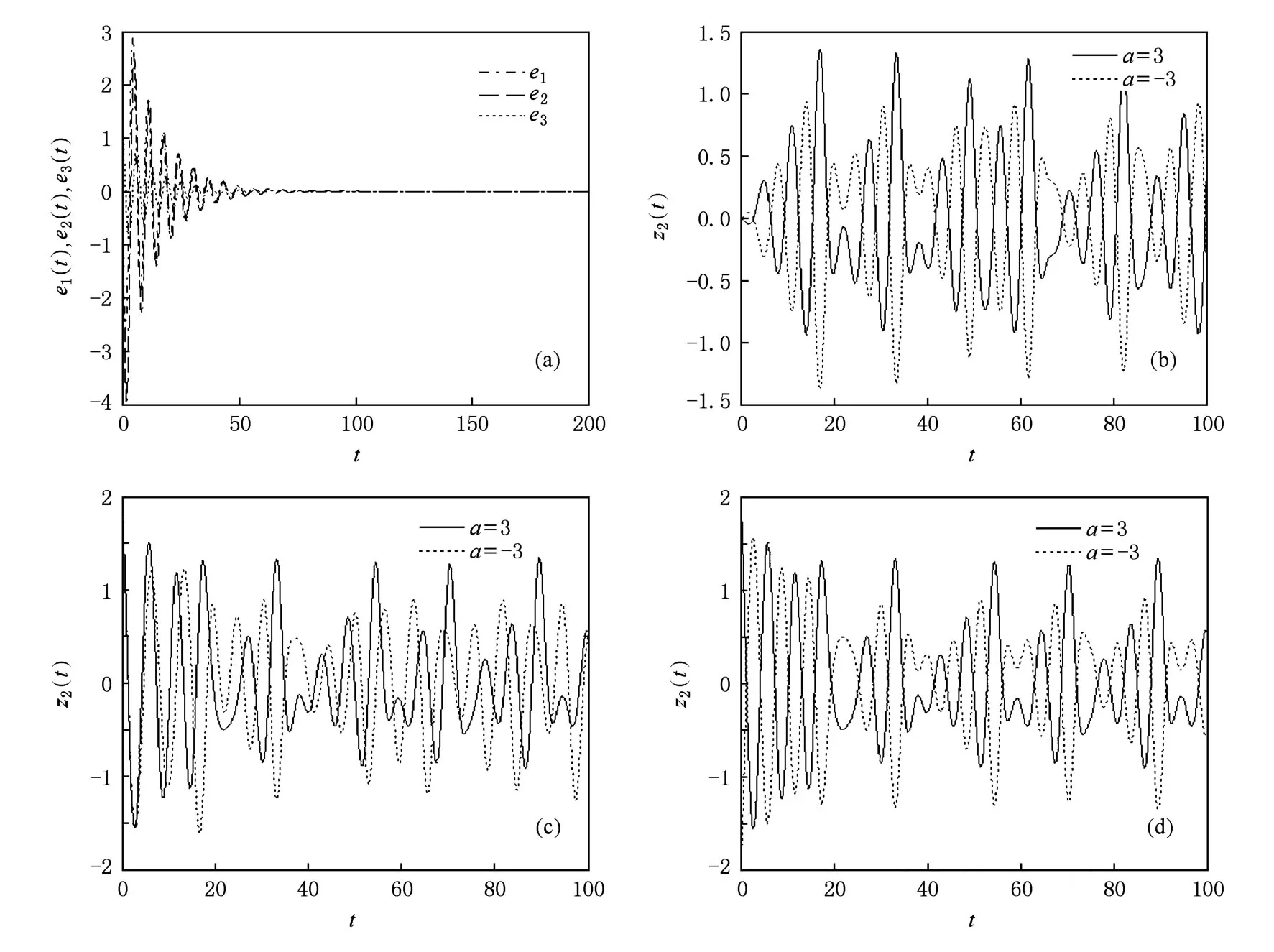
圖3 參數a的倒相控制作用 (a)a=-3時的同步誤差曲線,(b)信號z2(t)(初始值(-1,1,0)),(c)信號z2(t)(初始值中z0坐標不隨a變極性),(d)信號z2(t)(初始值中z0坐標隨a變極性)

3.2.廣義投影同步:λ=k≠1

(10)式指出,當選擇不同的λ時,響應系統的狀態變量將是驅動系統的對應狀態變量的λ倍,也就是響應系統與驅動系統之間實現了廣義投影同步.不妨將響應系統與驅動系統之間狀態變量的誤差定義為e1=x2-λx1,e2=y2-λy1,e3=z2-λz1.設置參數a=d=3,b=0.4,c=1.62,β=0.5, λ=-2,驅動系統與響應系統的初值分別為(1,-1,0)和(-1,1,0)時,采用ODE45算法,得到響應系統與驅動系統的同步效果,如圖4所示.討論λ取不同值的情況,分析同步體系的輸出信號波形,驗證響應系統與驅動系統之間實現廣義投影同步,有:當λ>1時,響應系統實現對驅動系統輸出信號的同相放大,如圖5(a)所示;當λ<-1時,響應系統實現對驅動系統輸出信號的倒相放大,如圖5(b)所示;當0<λ<1時,響應系統實現對驅動系統輸出信號的同相縮小,如圖5(c)所示;當-1<λ<0時,響應系統實現對驅動系統輸出信號的倒相縮小,如圖5(d)所示.

注意到,當選擇λ=-2時,響應系統(9)的輸出狀態在變成驅動系統(5)的2倍的同時,響應系統的狀態變量也將與驅動系統的狀態變量保持反相關系,如圖4(c),(d)和圖5(b)所示,這正是廣義投影同步中比例因子的作用.可見,這里的λ起到調整同步體系內部響應、驅動系統狀態變量之間的比例關系(包括幅度關系與相位關系)的作用,也是一種比例因子,但要注意這種同步比例因子是響應系統與驅動系統之間的比例,而不是驅動系統與響應系統之間的比例[31],在數值上兩者有倒數的關系.

圖4 響應系統與驅動系統實現廣義投影同步 (a)狀態變量相圖y1-y2,(b)同步誤差曲線e(t),(c)同步體系的混沌吸引子在x-y的平面投影,(d)同步體系的混沌吸引子在x-z的平面投影

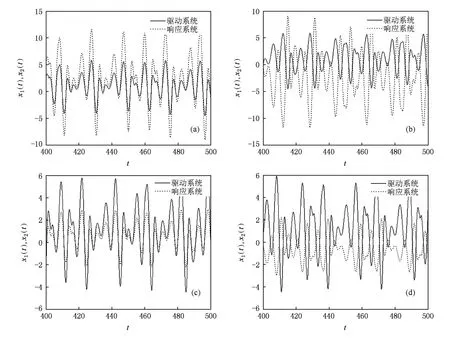
圖5 同步體系的狀態變量x(t)波形 (a)λ=2,(b)λ=-2,(c)λ=0.5,(d)λ=-0.5

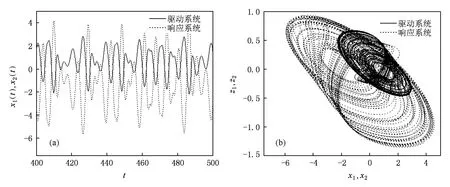
圖6 d=1.5時的同步情況 (a)狀態變量波形x(t),(b)混沌吸引子在x-z平面的投影

根據前面分析,恒指數譜混沌系統中存在的全局線性調幅參數d,同樣可以對廣義投影同步體系中兩個子系統狀態變量的幅度實施同步升降控制.如圖6所示,當同步體系中的d=3更改為d=1.5時,接著前面的λ=-2時的廣義投影同步進行討論,在響應與驅動兩個子系統建立同步關系以后,同步體系輸出的混沌信號相比于d=3的情況得到了縮小(圖6(a)與圖5(b)相比較),同步體系中響應與驅動系統輸出的混沌吸引子相比于d=3的情況也有了等比例的壓縮(圖6(b)與圖4(d)相比較).倒相參數也同樣可以對同步體系中響應與驅動兩個子系統中狀態變量z(t)信號的相位實施同步倒相控制(同樣要注意初始值中的z0坐標的設定,因為初始狀態是外界設置的,不是系統的自然狀態),如圖7所示.當同步體系中的a由a=3更改為a=-3時,接著上面的λ=-2時的廣義投影同步進行討論,在響應與驅動兩個子系統之間建立起同步關系以后,同步體系輸出的混沌信號z(t)相比于a=3的情況受到了倒相控制,如圖7(a)和(b)所示,由于a的倒相作用,原來的波峰變成了波谷,波谷變成了波峰;當然,同步體系輸出的混沌吸引子也在z方向有了顛倒(比較圖7(d)與圖4(d)),而在x與y向保持不變(比較圖7(c)與圖4(c)).

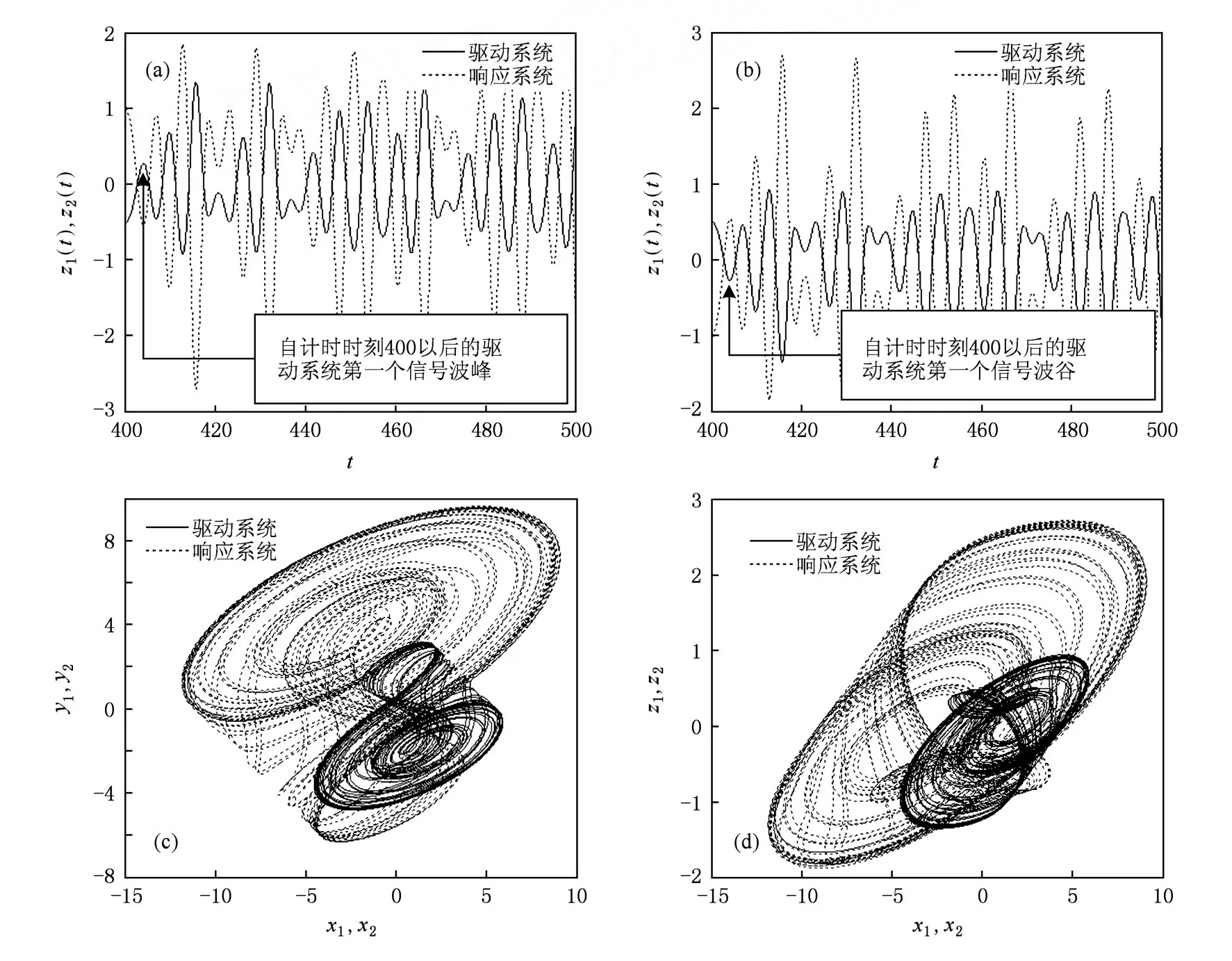
圖7 同步體系的倒相控制 (a)a=3時的狀態變量波形z(t),(b)a=-3時的狀態變量波形z(t),(c)a=-3時的混沌吸引子在x-y的平面投影,(d)a=-3時的混沌吸引子在x-z的平面投影

綜上所述,恒指數譜混沌系統的兩個獨特參數全局線性調幅參數d與倒相參數a增加了同步體系新的可控性,全局線性調幅參數d起到外部同步調整狀態變量幅值的作用,倒相參數a對同步體系兩個子系統的狀態變量z(t)進行同步倒相控制.對于廣義投影同步而言,由于存在調節響應系統與驅動系統狀態變量之間比例關系的比例因子λ,因此,不妨將這兩個具有特殊控制作用的參數定義為同步體系的外部控制因子,全局線性調幅參數d是狀態變量幅度外控因子,而倒相參數a是其中狀態變量z(t)的倒相外控因子.通過同步體系中比例因子λ、幅度外控制因子d以及相位外控因子a等三個參數的協同作用,可以容易地實現同步體系狀態變量的幅度與相位的靈活控制.

4.電路實驗仿真

上述基于廣義同步理論構建的恒指數譜同步體系只包含驅動系統與響應系統兩個部分,系統結構簡單,電路容易實現.同步體系中驅動系統固定,通過選擇不同的與系數矩陣對易的矩陣,構造不同的響應系統,從而實現完全同步、廣義投影同步以及一般的廣義同步.驅動系統的電路設計直接采用文獻[29]所提供的電路模型,這里不再重復.響應系統的電路設計也基于同樣的結構,根據(9)式,只要添加合適的線性反饋項與非線性反饋項即可實現,具體電路如圖8所示.

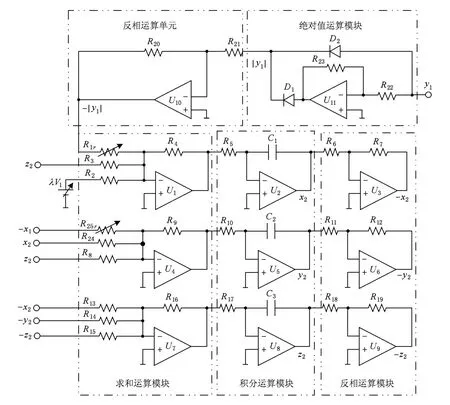
圖8 同步體系中響應系統的電路結構

根據電路理論以及各元件的特性,可以得到圖8電路的狀態方程為

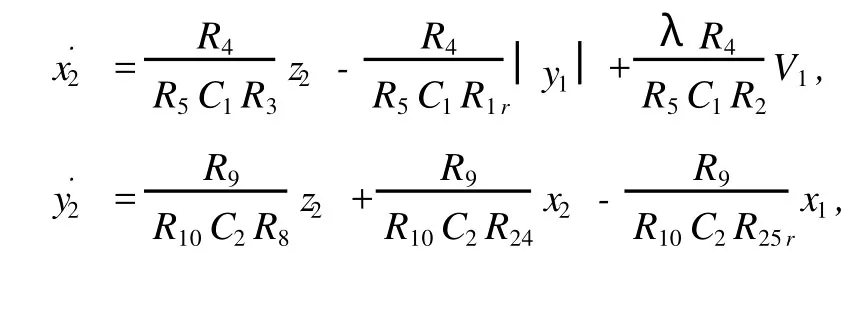
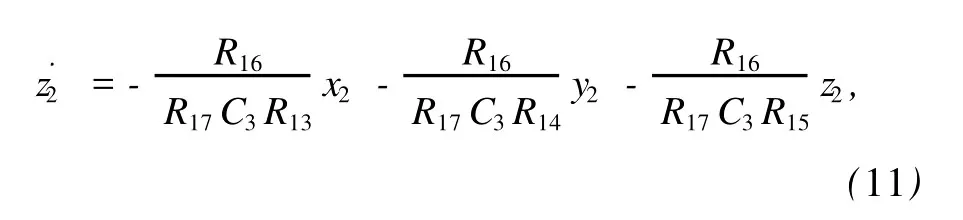
與響應系統的電路方程一致.當同步系統參數取a =3,b=0.4,c=1.62,d=3時,對應地設置電路元器件參數為:C1=C2=C3=1μF,R1= 27.778 kΩ,R2=45 kΩ,R3=15 kΩ,R4=900Ω, R5=20 kΩ,V1=3 V,R8=15 kΩ,R9=900 kΩ, R10=20 kΩ,R13=R14=120 kΩ,R15=50 kΩ,R16=400Ω,R17=20 kΩ,其他反相器的電阻都統一設置為1 kΩ.為表示方便,圖中響應系統與驅動系統的相同部分采用同名電阻、運放或者信號,不同部分(包括新增部分)采用不同的標識.響應系統的特殊參數要根據同步要求與不同的同步方法來設置.當β=0.5時,設置R24=90 kΩ;對應不同的λ值,選擇R1r=(27.778/|λ|)kΩ,R25r=(90/|λ|) kΩ來實現(當λ為負數時,要同時將反饋信號的極性作對應的調整);響應系統的直流電源大小也根據λ來設定,當λ為負數時,也要同時將電源極性顛倒.

由于廣義投影同步中,當λ=1時,就是完全同步.因此,限于篇幅,這里只討論一般的廣義投影同步的電路實驗.令λ=-2,也就是將響應系統參數設置為R1r=13.889 kΩ,并將相應支路的反饋信號-|y1|改為|y1|;R25r=45 kΩ,并將相應支路的反饋信號-x1改為x1;響應系統中的直流輸入電壓相應調整為-6 V,這樣構建的響應系統與驅動系統實現廣義投影同步,同步效果如圖9所示;同步體系中響應系統與驅動系統的混沌波形如圖10所示(明線為驅動系統的狀態波形,暗線為響應系統的狀態波形),由圖10可見,當λ=-2時,同步實現以后,響應系統的狀態變量是驅動系統對應狀態變量的倒相放大;響應系統的混沌吸引子如圖11所示.當同步體系中的d由3調整至1.5時,在建立起同步以后,響應系統的混沌吸引子如圖12所示,與圖11比較可見,d縮小一倍,相應的混沌吸引子之跌宕區間在橫、縱坐標方向都縮小了一倍.調整同步電路中的參數a,使之極性改變(這通過對電路中的反饋信號進行調整來實現),從而得到相應的混沌吸引子如圖13所示.比較圖13與圖11可見,由于a的極性改變,使得混沌吸引子在z方向上顛倒了一下,圖14給出的混沌波形(同樣明線代表驅動系統,暗線代表響應系統),進一步驗證了a的極性改變對z(t)信號的倒相作用.觀察圖14(c)與圖10(c)發現,在z(t)波峰的地方變成了波谷,波谷的地方也變成了波峰,而圖14(a),(b)與圖10(a),(b)相比,沒有波峰與波谷的轉換,也說明a的極性改變對x(t)與y(t)信號沒有倒相作用.以上結果驗證了全局線性調幅參數d與倒相參數a對于同步體系的幅度與相位的控制作用,與前面的數值仿真結果一致.

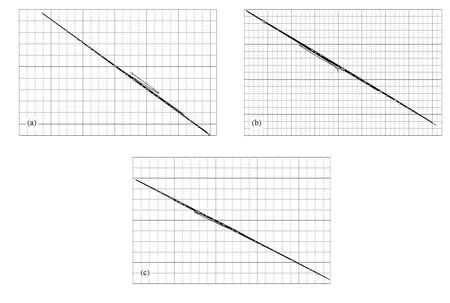
圖9 電路同步實驗狀態變量相圖 (a)x1-x2(橫坐標0.5 V/div,縱坐標2 V/div),(b)y1-y2(橫坐標0.2 V/div,縱坐標1 V/div),(c)z1-z2(橫坐標0.1 V/div,縱坐標0.5 V/div)

圖10 電路同步實驗觀察到的狀態變量波形圖 (a)x(t)(橫坐標5 s/div,縱坐標2 V/div),(b)y(t)(橫坐標5 s/div,縱坐標1 V/div),(c)z(t)(橫坐標5 s/div,縱坐標0.5 V/div)

圖11 響應系統混沌吸引子(d=3) (a)x2-y2的平面投影(橫縱坐標1 V/div),(b)x2-z2的平面投影(橫坐標1 V/div,縱坐標0.5 V/div),(c)y2-z2的平面投影(橫縱坐標0.5 V/div)

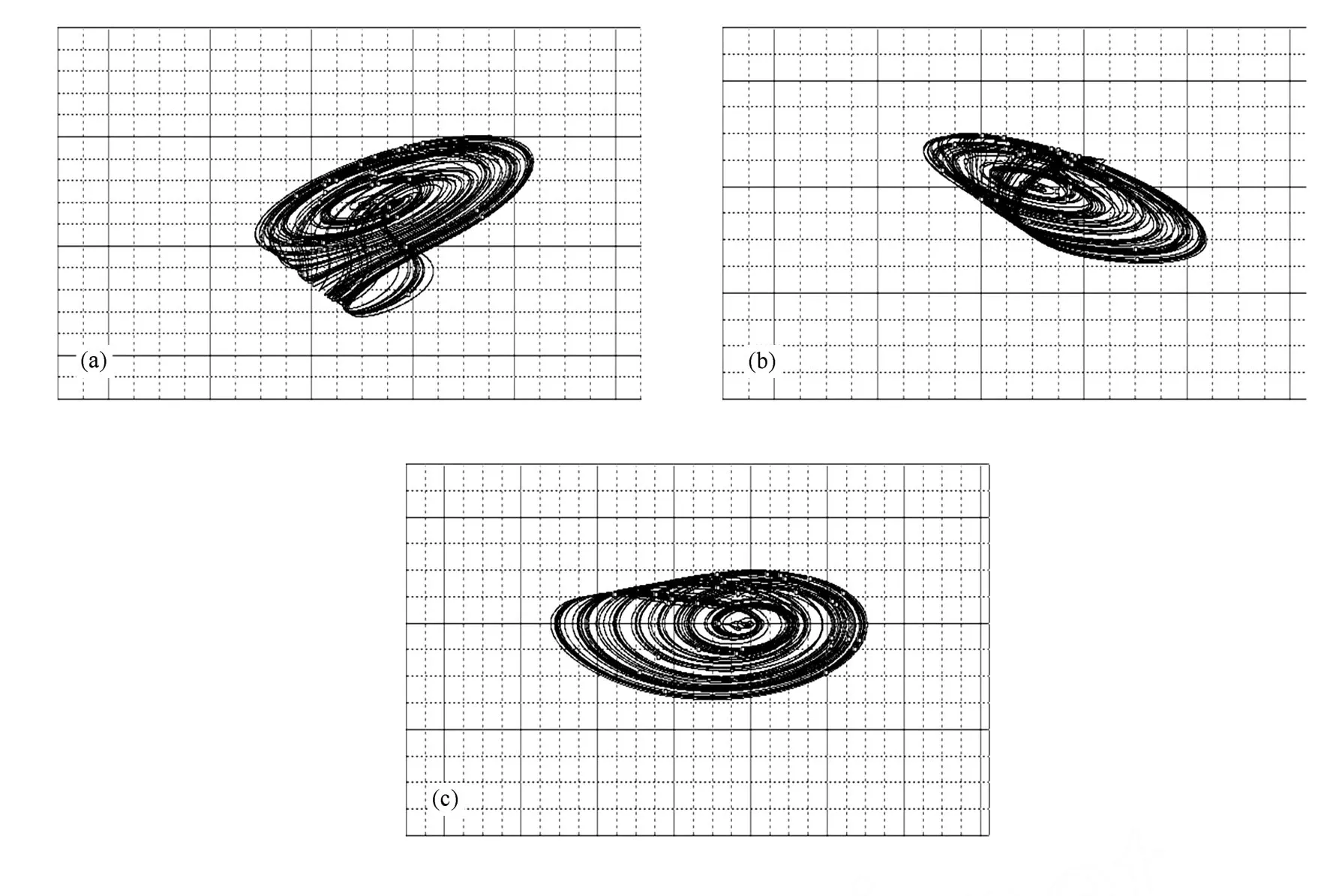
圖12 響應系統混沌吸引子(d=1.5) (a)x2-y2的平面投影(橫縱坐標1 V/div),(b)x2-z2的平面投影(橫坐標1 V/ div,縱坐標0.5 V/div),(c)y2-z2的平面投影(橫縱坐標0.5 V/div)

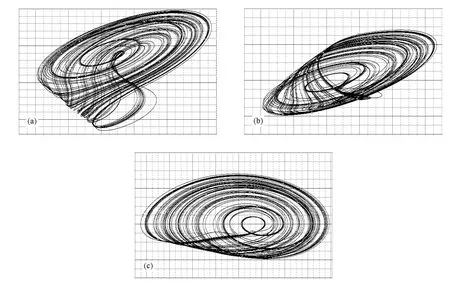
圖13 響應系統混沌吸引子(a=-3) (a)x2-y2的平面投影(橫縱坐標1 V/div),(b)x2-z2的平面投影(橫坐標1V/ div,縱坐標0.5 V/div),(c)y2-z2的平面投影(橫縱坐標0.5 V/div)

圖14 電路同步實驗狀態變量波形圖(a=-3) (a)x(t)(橫坐標5 s/div,縱坐標2 V/div),(b)y(t)(橫坐標5 s/div,縱坐標1 V/div),(c)z(t)(橫坐標5 s/div,縱坐標0.5 V/div)

5.結 論

根據恒Lyapunov指數譜混沌系統的特殊結構,可以得到該系統新的同步方法;從該系統的特殊參數出發又可得到其同步體系的新調節因子.本文基于廣義同步的基本原理,構造合適的驅動系統與響應系統,研究了恒Lyapunov指數譜混沌系統的同步方法;從廣義同步引申開去,通過改變響應系統的一些參數,實現了恒指數譜混沌系統的完全同步與廣義投影同步.改進恒Lyapunov指數譜混沌系統的同步體系具有三個重要的調節因子,全局線性調幅參數d能對驅動與響應系統的狀態變量幅值實施同步升降控制,倒相參數a能對某一特定狀態變量z(t)實施同步倒相控制,而比例因子λ則對響應系統與驅動系統狀態變量之間的幅度與相位關系進行內部鎖定與控制.全局線性調幅參數d(幅度調節器)與倒相參數a(相位調節器)是外調節因子,比例因子(幅相鎖定器)是內調節因子,內外調節因子的協同作用,使得改進恒Lyapunov指數譜混沌系統的同步體系更加靈活、可控.數值仿真與實驗仿真驗證了上述同步方案的正確性與可實施性,也驗證了內外三個調節因子各自的控制與調節作用.

[1]HuW,Liu Z,Li C B 2008IEEE Trans.Aero.Electr.Sys.44 367

[2]Liu Z,Zhu X H,HuW 2007Int.J.B ifurcat.Chaos17 1735

[3]Kolumbán G,KennedyM P,Chua L O 2002IEEE Trans.Circ. Syst.I45 1129.

[4]Pecora L M 1990Phys.Rev.Lett.64 821

[5]Maggio GM,diBernardoM 2000IEEE Trans.Circ.Syst.I47 1160

[6]Carroll TL,Pecora L M 1991IEEE Trans.Circ.Sys.38 453

[7]Par mananda P 1998Phys.Lett.A 240 55

[8]Wang F Q,Liu C X 2006Acta Phys.Sin.55 5055(in Chinese)[王發強、劉崇新2006物理學報55 5055]

[9]Zhu Z Y 2006Acta Phys.Sin.55 6248(in Chinese)[朱志宇2006物理學報55 6248]

[10]Wang F Z,Qi G Y,Chen Z Q,Zhang Y H,Yuan Z Z 2006 Acta Phys.Sin.55 4005(in Chinese)[王繁珍、齊國元、陳增強、張宇輝、袁著祉2006物理學報55 4005]

[11]WangX Y,Meng J 2008Acta Phys.Sin.57 0726(in Chinese) [王興元、孟 娟2008物理學報57 0726]

[12]Guan X P,Fan Z P,Peng H P,Wang Y Q 2001Acta Phys. Sin.50 2108(in Chinese) [關新平、范正平、彭海朋、王益群2001物理學報50 2108]

[13]Li G H,Zhou S P 2007Chaos Soliton.Fract.32 516

[14]Jia Z,Lu J A,Deng G M,Zhang Q J 2007Chin.Phys.16 1246

[15]Li C B,WangD C 2009Acta Phys.Sin.58 764(in Chinese) [李春彪、王德純2009物理學報58 764]

[16]Hu J,ZhangQ J 2008Chin.Phys.B 17 503

[17]Wu X J,Lu H T,Shen SL 2009Phys.Lett.A 373 2329

[18]Mainieri R,Rehacek J 1999Phys.Rev.Lett.82 3042

[19]Li Z G,Xu D L 2001Phys.Lett.A 282 175

[20]Xu D L 2001Phys.Rev.E 63 27201

[21]Wang X Y,Wang Y 2007Acta Phys.Sin.56 2498(in Chinese)[王興元、王 勇2007物理學報56 2498]

[22]Yan J P,Li C P 2005Chaos Soliton.Fract.26 1119

[23]Li G H 2006Chaos Soliton.Fract.30 77

[24]Feng C F,Zhang Y,Sun J T,QiW,Wang Y H 2008Chaos Soliton.Fract.38 743

[25]Peng G J,Jiang YL,Chen F 2008Phys.A 387 3738

[26]Li C P,Yan J P 2006Chaos Soliton.Fract.30 140

[27]Min F H,Wang Z Q 2007Acta Phys.Sin.56 6238(in Chinese)[閔富紅、王執銓2007物理學報56 6238]

[28]Guo L X,Xu Z Y,HuM F 2008Chin.Phys.B 17 4067

[29]Li C B,Chen S,Zhu H Q 2009Acta Phys.Sin.58 2255(in Chinese)[李春彪、陳 謖、朱煥強2009物理學報58 2255]

[30]Li C B,Wang H K 2009Acta Phys.Sin.58 7514(in Chinese) [李春彪、王翰康2009物理學報58 7514]

[31]Li C B,Shan L,WangD C 2009Acta Phys.Sin.58 6016(in Chinese)[李春彪、單 梁、王德純2009物理學報58 6016]

[32]KocarevL,ParlitzU 1996Phys.Rev.Lett.76 1816

[33]Gao Y,Weng J Q,Luo X S,Fang J Q 2002J.Electr.Infor m. Tech.24 855(in Chinese)[高 遠、翁甲強、羅曉曙、方錦清2002電子與信息學報24 855]

Li Chun-Biao1)2)?Hu Wen3)

1)(Department of Engineering Technology,Jiangsu Institute of Econom ic and Trade Technology,Nanjing 210007,China)

2)(Department of Electric Source and System,Research and Development Center of Food Safety Engineering Technology of Jiangsu Province,Nanjing 210007,China)

3)(School of Infor mation Science and Technology,Nanjing University of Aeronautics and Astronautics,Nanjing 210016,China)

PACC:0545

Synchronization methods and properties of the improved chaotic system with constantLyapunov exponent spectrum＊

6 May 2009;revised manuscript

9 June 2009)

The existence of special piecewise-linear structure,global linear amplitude adjuster and phase-reverse controller in improved chaotic system with constant Lyapunov exponent spectrum contributed much to finding new synchronization methods and new adjusting parameters.According to the principle of generalized synchronization,by constructing appropriate driving system and response system,generalized synchronization of the improved chaotic system with constant Lyapunov exponent spectrum then can be achieved.By changing the parameter of response system,the complete synchronization and generalized projective synchronization can be further realized.The amplitude of the state variable of the driving system and the response system can be controlled to increase and decrease synchronously by the global linear amplitude adjuster,while the phase of certain variables can be controlled to reverse synchronously by the phase-reverser. This synchronization system dispenseswith other special controllers,possesses simple structure and so can be implemented easily.Finally,the implement circuit of synchronization system is designed.It is validated by experiment simulation that the synchronization methods are feasible,the amplitude and the phase of the state variable in the synchronization system can be controlled by special parameters of the improved chaotic system.

improved chaotic system with constant Lyapunov exponent spectrum,synchronization,amplitude control, phase-reverse control

＊江蘇省“青藍工程”(批準號:蘇教師[2008]30號)和航空基金(批準號:2009ZC52038)資助的課題.

?E-mail:goontry@126.com

＊Project supported by the QingLan Project of Jiangsu Province,China(Grant No.[2008]30)and the Aeronautical Science Foundation of China (GrantNo.2009ZC52038).

?E-mail:goontry@126.com