利用陣發混沌現象測定未知信號參數
翟篤慶 劉崇新 劉 堯 許 喆
(西安交通大學電氣工程學院,西安 710049)
利用陣發混沌現象測定未知信號參數
翟篤慶?劉崇新 劉 堯 許 喆
(西安交通大學電氣工程學院,西安 710049)
(2009年5月12日收到;2009年6月17日收到修改稿)
利用Duffing方程對頻率的極端敏感性產生陣發混沌現象,研究了一種利用該現象定量檢測未知的微弱周期信號的各項參數的新方法,通過理論分析和實例仿真證明了該方法的可行性,并針對仿真結果提出了改進措施,提高了檢測精度.
Duffing方程,陣發混沌,檢測信號參數
PACC:0545
1.引言
信號處理領域的一個重要研究課題是對未知信號的各項參數的測定,包括頻率、幅值和相位,這在工程應用中有著重要的實際意義.近年來,混沌同步的思想被科學工作者們應用于未知參數的辨識中.文獻[1]利用狀態觀測器實現了不確定的Lü系統的混沌控制和參數辨識.文獻[2]對一類不確定參數的復雜網絡提出了自適應同步方法.文獻[3—6]分別以不確定參數的Chen系統、超混沌Chen系統、Lorenz-like系統和R?ssler系統為例,在實現自適應同步的同時,辨識了未知參數.文獻[7]則以Gray-Scott系統產生時空混沌,實現混沌同步和參數辨識.文獻[8]利用自適應法,實現了Duffing等系統的混沌同步和參數辨識.文獻[9]研究了不確定Liu系統的混沌同步和參數辨識.文獻[10]則把自適應同步和參數辨識的原理和思想應用到混沌保密通信中,獲得加密系統的參數.這些成果不僅實現了不確定混沌系統之間的同結構和異結構同步,完善了混沌同步的理論,也為不確定系統的未知參數辨識找到了方法.但目前該方法的研究主要集中于自治系統的未知系數(包括非自治系統的周期信號的幅值)的辨識,對于非自治系統的頻率和相位參數,尚沒有行之有效的確定方法.本文針對Duffing方程,基于另一種思想,尋求找到確定Duffing系統中時間變量的頻率和相位參數的方法.另外,人們在對混沌理論的研究中發現:一類混沌系統在一定條件下對小信號具有極端的敏感性而同時對噪聲具有很強的免疫力,這使得此類混沌系統在信號檢測領域中具有廣闊的應用前景.著名的Duffing振子就具有這種特性,當其處于混沌分岔區域附近時,對臨近頻率的微弱信號敏感而對強噪聲免疫.這使得該方法在強噪聲背景下同樣有效.文獻[11]在對Duffing系統的研究過程中,發現了由于對頻率參數的敏感性,導致系統狀態時而周期,時而混沌,像呼吸一樣時斷時續,并且“呼”與“吸”都有固定的時間跨度,故稱其“breather”.文獻[12]提出了Duffing方程右側的周期策動力幅值的敏感性,即存在某個臨界值,幅值稍大于該臨界值時就會呈現大尺度周期狀態,小于該臨界值時則呈現混沌狀態,并把對于該敏感性的檢測用于測定某已知頻率的信號幅值.文獻[13]通過計算周期狀態時一段時間內的過零點次數來確定未知信號頻率.文獻[14]和[15]提出在Duffing方程右側加上策動力頻率附近的微弱信號后,會產生陣發混沌現象,策動力幅值會隨時間變化.當幅值大于文獻[12]中的臨界值時,呈現大尺度周期運動狀態,小于該臨界值時,呈現混沌狀態,這樣就會出現時而周期,時而混沌的運動狀態,把這種現象稱為陣發混沌現象.通過觀察該現象是否發生來判斷待測信號中是否存在與策動力頻率相近的周期信號.文獻[16]對一個帶有外部擾動的Duffing方程進行了詳盡的分析,包括其最大Lyapunov指數、分叉情況和陣發特性等.
在前人研究的基礎上,本文在Duffing方程的右端施加諧振擾動,產生陣發混沌現象,分析了擾動后的系統狀態的變化情況.通過對該現象的觀測和測定,確定施加的待測信號的各項參數,包括頻率、幅值和相位.仿真實驗得到了較為精確的結果,證明了該方案的可行性,且對多頻信號同樣適用.
2.陣發混沌現象的理論分析和仿真
經典的Duffing方程為
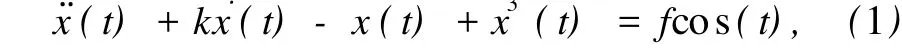
式中x(t)為狀態變量,k為阻尼比,fcos(t)為周期策動力,-x(t)+x3(t)為非線性恢復力.改寫為如下動力學方程:
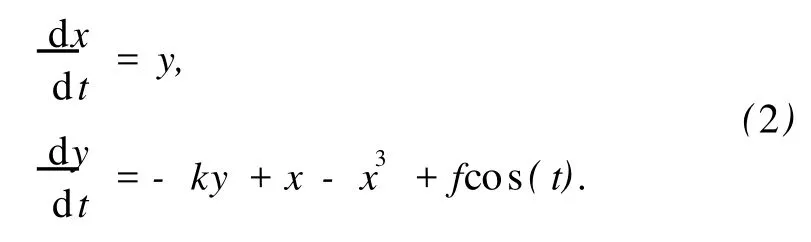
當k=0.3時,改變參數f的取值,觀察系統的x-y相圖,會發生如圖1所示的狀態變化.使系統從混沌狀態轉變到大尺度周期狀態的參數f的臨界值Fc∈(0.53492,0.53493).從圖2所示分叉圖中也可看出狀態變化的臨界值范圍.
令t=ω τ,f=F0,(1)式可改寫為
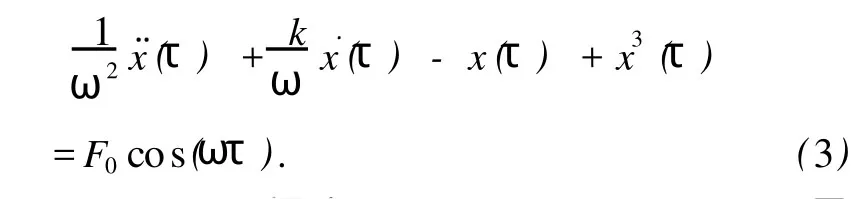
在(3)式右側加上頻率ω附近的待測周期信號
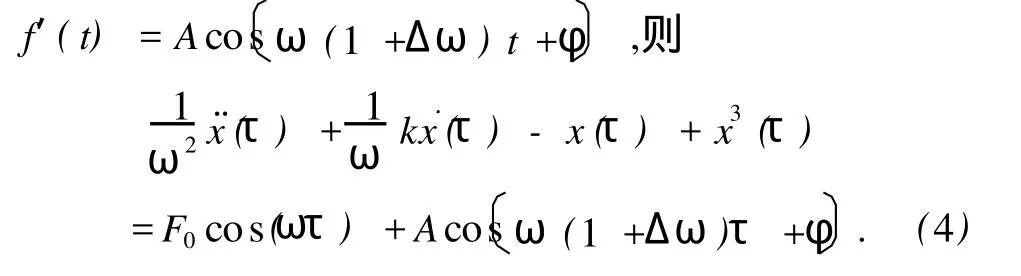
對(4)式右側化簡
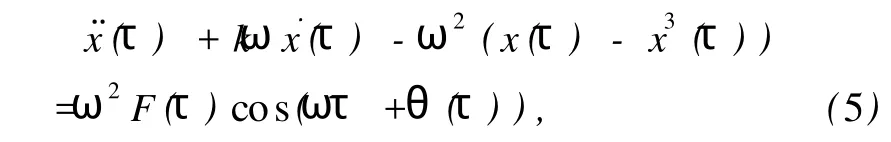
其中
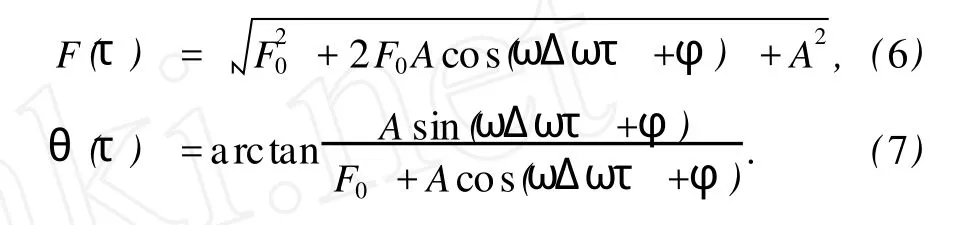
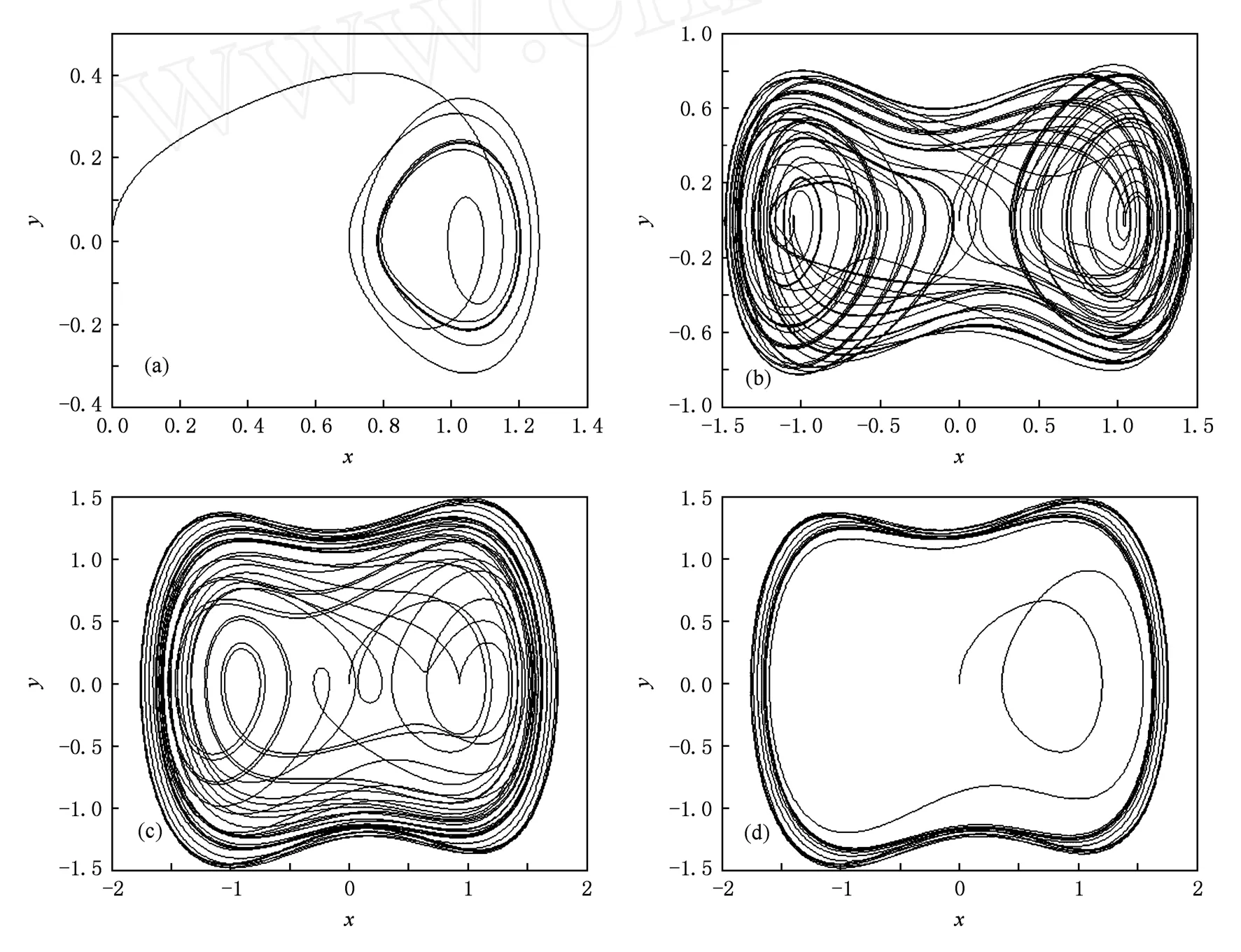
圖1 參數f改變引起的系統x-y相圖變化 k=0.3.(a)f=0.2,(b)f=0.35,(c)f=0.53492,(d)f=0.53493
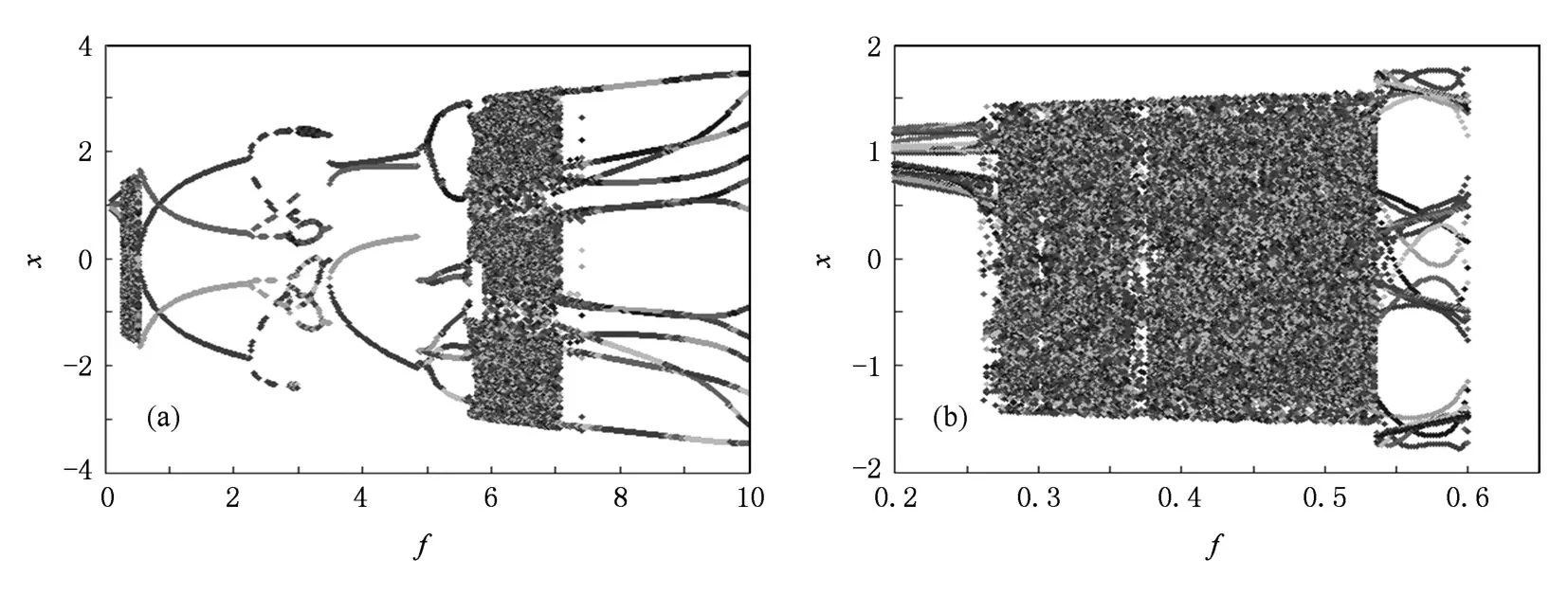
圖2 Duffing方程x變量隨參數f變化的分叉圖 k=0.3.(a)f∈(0,10),(b)f∈(0.2,0.65)
觀察(5)式與(1)式,當ω=1時,二者差別在于(5)式中多出了一個參數相位角.文獻[17]討論了相位為隨機噪聲時對系統狀態變化的影響.這里的相位是與幅值相關的函數,考慮其影響系統狀態的情況.
由(6)式得到
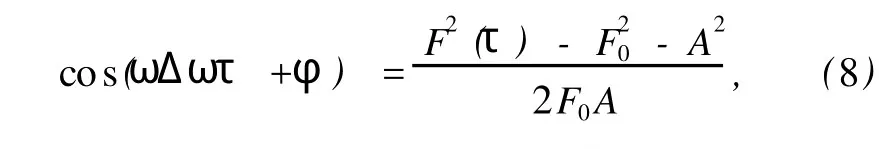
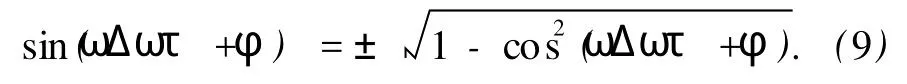
把(8)和(9)式代入(7)式中,令θ(τ)=g(F(τ)),得
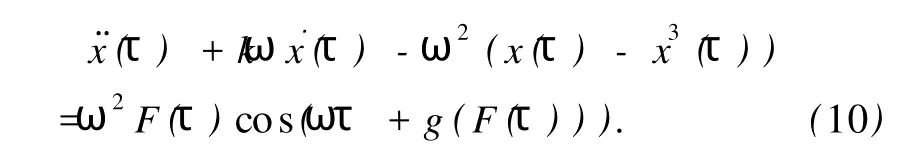
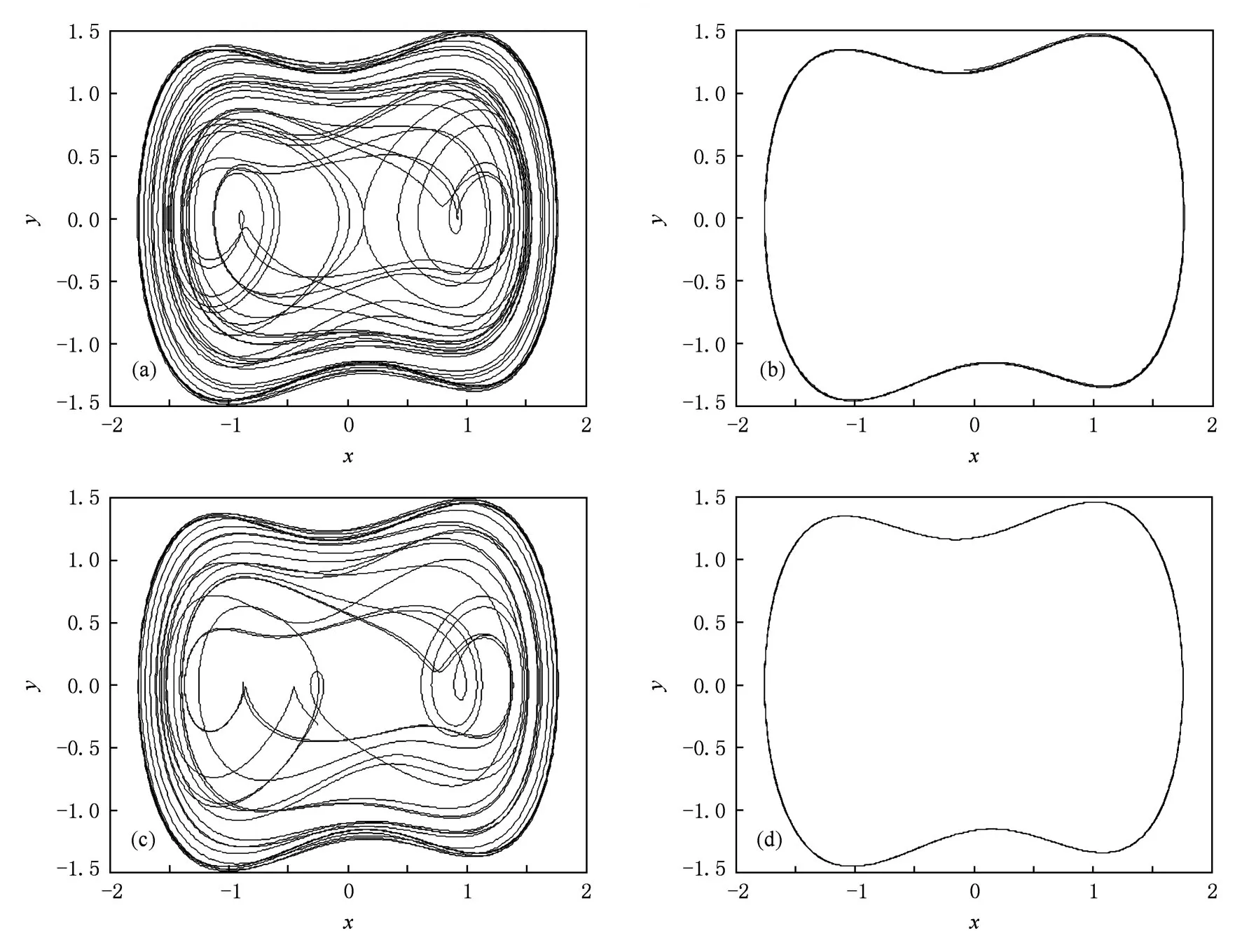
圖3 F(τ)引起的x-y相圖變化 (a)F(τ)=0.5413((9)式取正號),(b)F(τ)=0.5414((9)式取正號),(c)F(τ) =0.537((9)式取負號),(d)F(τ)=0.5371((9)式取負號)
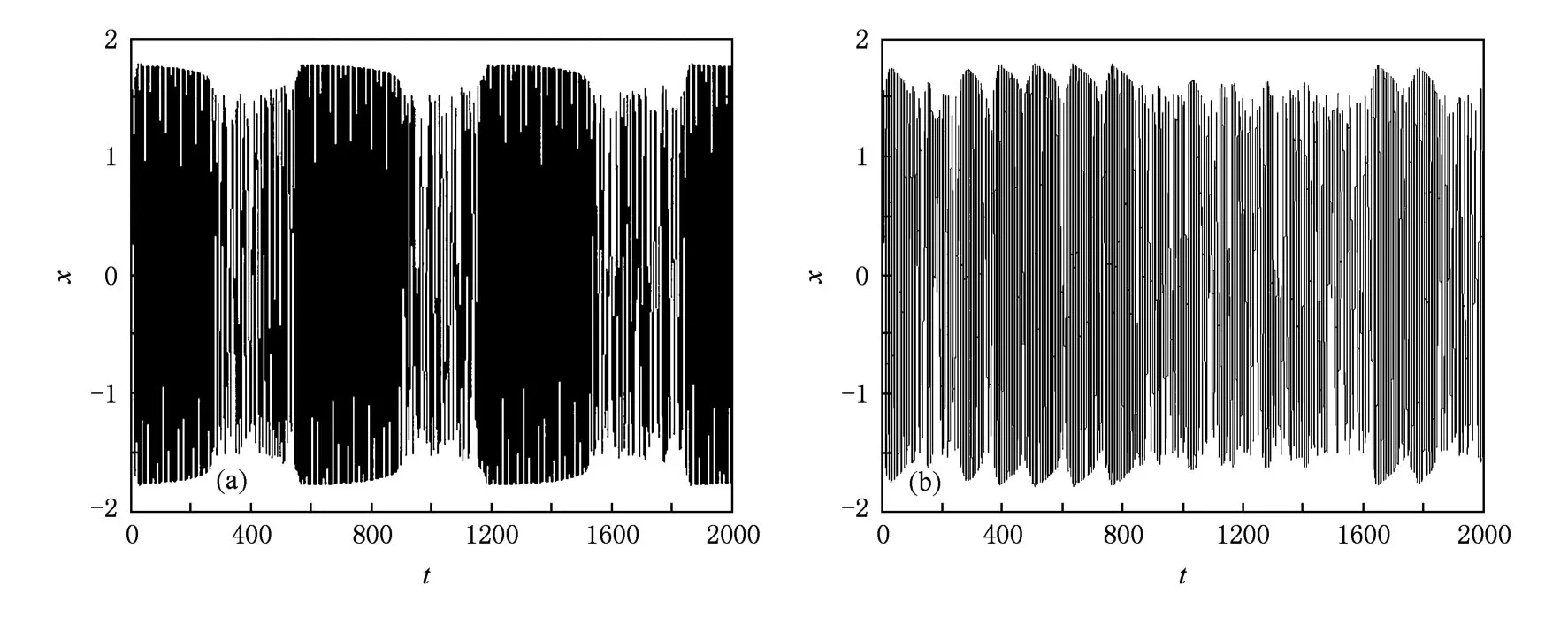
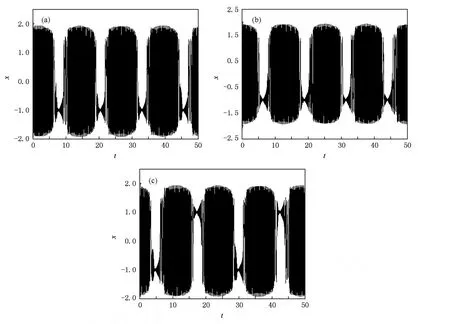
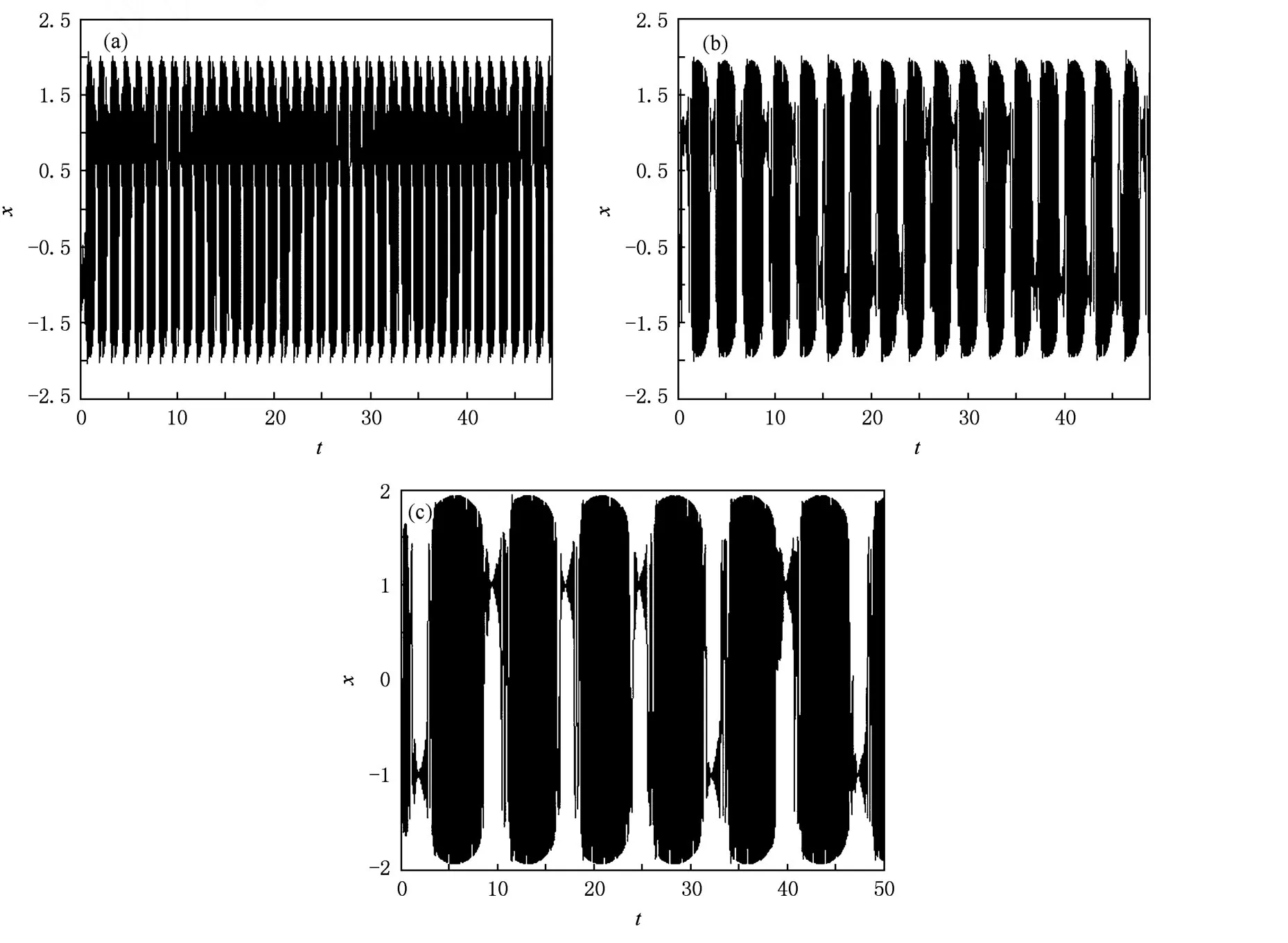
取F0=0.52,A=0.1,k=0.3,ω=1,由(6)式考慮到F(τ)∈(F0-A,F0+A)=(0.42,0.62),觀察系統狀態變化情況(見圖3和圖4).發現存在臨界值Fc,當(9)式取正號時,Fc∈(0.5413, 0.5414),當(9)式取負號時,Fc∈(0.537, 0.5371),當F(τ)>Fc時,系統處于周期狀態;當F(τ) 由于F(t)的取值會隨著時間t變化,時而大于Fc,時而小于Fc,(10)式所描述的系統就會呈現混沌狀態和周期狀態交替出現的情況,這就是陣發混沌現象.令F0=0.52,A=0.04,ω=1,Δ ω=0.01,通過時域信號圖可以清晰地觀察到陣發混沌現象(見圖5(a)). 圖4 (10)式中變量x隨F(τ)變化的分叉圖 (a)(9)式取正號,(b)(9)式取負號 圖5 陣發混沌現象 (a)Δ ω=0.01,(b)Δ ω=0.05 這里需要注意的是Δ ω不可以過大或過小.過小時,F(t)變化緩慢,導致陣發混沌現象的每個混沌狀態和周期狀態跨度過大,要檢測出相對頻差就需要大大增加采樣和計算的工作量;另外,由于系統完成狀態變化通常需要1個周期以上的時間,當Δ ω過大時,F(t)變化過快,系統完成相變的過程中沒有足夠長時間的激勵,系統無法很好地響應如此快的變化,陣發混沌現象失去原有的規律性.通過仿真實驗,我們一般取Δ ω∈(0.005,0.04). 加上待測信號后的策動力幅值f在臨界值Fc附近隨時間變化 若要檢測頻率ω′∈(ω1,ω2)的待測信號,先選取合適的公比1+Δ ω,從ω1開始以公比1+Δ ω取值作為周期策動力的頻率,檢測陣發混沌現象是否發生,如果發生就用上述方法算出ω′,若一直沒有發生則說明不存在該頻率區間內的周期信號. 設當cos(ω Δ ωt+φ)=a,a∈0,1時,F(t) =Fc,則當cos(ω Δ ωt+φ)>a時,系統處于大尺度周期狀態,對應圖6中的T1時間段;當cos(ω Δ ωt+ φ) 設(4)式中的周期策動力為F0cos(ωt+φ1),待測信號Acos(ω(1+Δ ω)t+φ2),二者相位差Δ φ =φ2-φ1,但F(t)和θ(t)均有變化 假設相位差Δ φ=0,當t=0時,cos(ω Δ ωt+ Δ φ)=1,F(t)=F0+A>Fc,隨著時間變化,t= T1時,cos(ω Δ ωt+Δ φ)減小到a,F(t)從F0+A減小到Fc,系統從大尺度周期狀態進入混沌狀態.同樣的,如果cos(ω Δ ωt+φ)從a增加到1,相應的F(t)從Fc增加到F0+A,對應的,也需要時間T1.這樣,我們可以得到如下結論:當時,cos(ω Δ ωt+Δ φ)=1,系統處于大尺度周期狀態且正處于該狀態的時間中點,即該狀態恰好完成了一半.圖7所示的仿真結果,以時間零點觀察,圖7(b)圖中零點恰好為周期狀態進行到一半的時間點,證明了該結論. 圖6 系統分別處于大尺度周期和混沌狀態的時間段 找出系統由混沌進入大尺度周期狀態的時間t1和由大尺度周期狀態進入混沌狀態的時間t2,, 待測信號相位φ2=φ1+Δ φ. 由圖6所示關系得 其中,T1,T2分別是大尺度周期狀態和混沌狀態的持續時間. 對于(11)式描述的幅值隨時間變化的函數, F(t)=Fc為臨界值t為取到臨界值的時間點,所以得到函數關系 通過仿真結果找到T1,T2的值,代入(16)式中,解該方程即可求得待測信號幅值A. 先預估信號頻率ω′∈(45,55),從ω=45開始以公比1.03取值作為周期策動力的頻率,直到觀測到陣發混沌現象,若沒有發生陣發混沌現象,則不存在該頻率范圍的周期信號.圖8所示的是周期策動力頻率取不同值時(周期策動力相位取為0,幅值F0=0.53),x(t)的時域信號. 圖7 Δ φ不同時的時域信號圖 圖8 不同ω時的時域信號圖 (a)ω=45,(b)ω=47.74,(c)ω=49.17 通過時域信號圖可以看出,ω=47.74時陣發混沌現象周期尚不明顯,ω=49.17時發生了明顯且有規則的周期性陣發混沌現象.以ω=49.17作為周期策動力頻率,通過Matlab仿真結果(見表1)找出由混沌狀態向大尺度周期狀態轉變的時間點. 表1 混沌狀態向大周期狀態轉變的仿真結果 通過比較定向過零點間距,可以看出自t= 3.29后過零點間距變化很小,且漸漸趨于穩定,故認為t=3.29時F(t)開始超過Fc,判斷t=3.29為混沌狀態向大尺度周期狀態轉變的時間點. 同樣的方法找出t=11.08,18.81,26.10, 33.76,41.18,48.84,56.38,64.17,71.90也是混沌狀態向大尺度周期狀態轉變的時間點.求大周期的平均值T=7.62333,ω Δ ω=0.82420,待測信號頻率ω′=ω(1+Δ ω)=49.994. 通過仿真結果比較過零點間距(見表2),發現自t=8.49后過零點間距開始逐漸失穩,故認為t=8.49時F(t)開始小于Fc,判斷t=8.49為大尺度周期狀態向混沌狀態轉變的時間點,則t=5.89為大尺度周期狀態的時間中點,因此按照3.2節中所述方法,待測信號相位 表2 大尺度周期狀態向混沌狀態轉變的仿真結果 同樣的方法找出t=16.03,23.50,31.17, 38.71,46.38,53.72,61.39,69.06,76.60,84.07也是大尺度周期狀態向混沌狀態轉變的時間點,求出各個大尺度周期狀態的時間中點,然后測定相位 求得平均值φ′=0.4931π. 大尺度周期狀態結束的時間(見表2)減去開始的時間(見表1),得到大周期狀態的持續時間T1,多次求T1再求其平均值可得T1=4.994,混沌狀態的持續時間T2=T-T1=2.629,代入(16)式中,解得待測信號幅值A=0.5070.其中臨界值Fc= 0.537,周期策動力幅值F0=0.53. 實例2 待測信號f′(t)=0.8cos(100t+π) 預估待測信號頻率ω′∈(90,110),周期策動力頻率從ω=90開始以公比1.03遞增,發現ω= 98.35時出現規則的陣發混沌現象.設定周期策動力頻率為ω=98.35,步長Δt選取為0.005,通過仿真結果找出t=4.335,8.105,12.09,15.71,19.6, 23.30,27.27,30.975,34.745,38.67為混沌狀態向大尺度周期狀態轉變的時間點.求大周期的平均值待測信號頻率ω=ω(1+Δ ω)=99.997. 通過仿真結果找出t=7.335,11.07,14.97, 18.705,22.54,26.34,30.175,33.975,37.71, 41.61.多次求相位再求平均值得φ′=0.9087π. 大尺度周期狀態持續時間T1=2.94,混沌狀態的持續時間T2=T-T1=0.875,代入(16)式中,解得待測信號幅值A=0.8032.其中臨界值Fc= 0.537. 對于該多頻信號,先檢測ω=50附近,設置周期策動力頻率ω=49,周期策動力幅值F0=0.53,通過仿真結果求得大周期平均值T=6.2844,ω Δ ω =0.9998,待測信號頻率ω′=ω(1+Δ ω)= 49.9998.多次求相位再求平均值φ′=1.4294π.大尺度周期狀態持續時間T1=3.871,混沌狀態的持續時間T2=T-T1=2.4134,代入(16)式中,解得待測信號幅值A=0.3923. 為了提高其他頻率分量的檢測精度,把ω=50的分量從原信號中減去,即f″(t)=f′(t)-0.3923cos(49.9998t+1.4294π).然后再檢測ω= 100附近,設置周期策動力頻率ω=98,周期策動力幅值F0=0.53,通過仿真結果求得大周期平均值T =3.1422,ω Δ ω=1.9996,待測信號頻率ω′=ω(1 +Δ ω)=99.9996.多次求相位再求平均值φ′= 0.9310π.大尺度周期狀態持續時間T1=1.8585,混沌狀態的持續時間T2=T-T1=1.2837,代入(16)式中,解得待測信號幅值A=0.3177. f?(t)=f″(t)-0.3177cos(99.9996t+ 0.9310π),再設置周期策動力頻率ω=195,周期策動力幅值F0=0.53,通過仿真結果求得大周期平均值T=1.2442,ω Δ ω=5.0500,待測信號頻率ω′=ω(1+Δ ω)=200.0500.多次求相位再求平均值φ′=0.3044π.大尺度周期狀態持續時間T1= 0.7443,混沌狀態的持續時間T2=T-T1= 0.4999,代入(16)式中,解得待測信號幅值A= 0.2303. 通過實例仿真發現該方法測量相位的結果誤差較大,其原因如下: 1)系統從某個狀態向另一個狀態轉變的過程中,需要一定時間的激勵,一般情況下需要超過一個周期的穩定激勵才能發生狀態變化,使得測量結果較實際值有一定滯后. 2)該方法通過比較過零點間距判斷狀態,決定了系統狀態的起始點只能在過零點,而實際狀態變化則會在任意時間點完成,這也使得結果較實際值滯后. 3)(7)式中ω Δ ω決定了誤差大小,因此減小Δ ω,即減小每次搜索頻率的范圍,可以減小誤差. 表3是對實例2的參數進行改動后得到的實驗數據,表明了相位滯后的大小主要由ω Δ ω決定,受待測信號幅值和相位影響不大,因此在ω Δ ω測定后,可通過仿真實驗估算出滯后相位的大小.測量結果加上該滯后相位,即可得到較精確的相位值.如實例3,可對滯后相位的大小求平均值Δ φ= 0.0994π,改進后的相位測量值φ″=φ′+Δ φ= 1.0081π,大幅度提高了相位測量的精度. 表3 滯后相位與待測信號參數的關系 對待測信號幅值的測定,是建立在精確測得大尺度周期狀態和混沌狀態的起始點的基礎上的,這樣才可以準確得到大尺度周期狀態和混沌狀態的持續時間,代入(16)式中才能精確地求解出待測信號幅值.因此如何精確測出系統狀態起始點,是提高幅值測量精度的關鍵. 1)離散化時盡量選擇較小的步長,如果步長過大,則過零點間距的變化對系統狀態變化不夠敏感,影響狀態起始點的測量精度.但考慮到步長過小會影響算法的效率,因此如何選擇步長,要視實際情況而定. 2)當待測信號幅值較小時,通過過零點間距來判斷系統狀態變化的方法可能會失效,因為系統在F(t)稍大于Fc時,混沌狀態向周期狀態轉變時存在較長時間的過渡過程(見圖9,觀察過零點間距,趨于等距要在兩個周期以后),而系統在該時間點停留時間內無法完成狀態的變化,按照過零點間距的判定方法,誤認為該狀態仍是混沌狀態.另外,當A-F0>Fc時,(6)式中F(t)∈(A-F0,A+F0),系統將一直處于周期狀態,陣發混沌現象消失. 表4是對實例3的幅值參數進行改動得到的實驗數據,它反映了幅值過小或過大使得該方法失效的現象.因此使用該方法前,需保證待測信號幅值處于有效區間內,如果不滿足,則需先預估幅值,再放大或縮小使之處于有效區間.該區間由信號頻率ω′和周期策動力頻率ω決定,可在測出頻率后通過仿真實驗確定.表4中ω=98,ω′=100. 圖9 F(t)=0.55時的時域信號圖 表4 幅值測量誤差與實際幅值的關系 本文提出了一種利用陣發混沌現象來檢測未知信號各項參數的方法,包括頻率、幅值和相位,從而完整地還原待測信號.該方法的具體步驟如下: 1)將待測信號加到Duffing方程右側,取合適的步長對周期策動力和待測信號之和進行采樣. 2)在待測信號可能存在的頻率區間內取合適的公比,按等比區間進行遍歷搜索,若檢測到陣發混沌現象發生,則按3.1節所述方法確定信號頻率. 3)分別按照3.2節和3.3節所述方法測定待測信號幅值和相位. 4)對于多頻信號,每次將所得前一頻率分量的信號從方程右側減去,再在下一個頻率分量可能存在的區間進行搜索,如此重復上述步驟,確定所有頻率分量信號的各項參數. 理論分析和實例仿真都證明了該方法的可行性.Duffing方程的性質決定了該方法具有以下特點: 1)對信號中各頻率分量要先預估,可能存在頻率的區間要取到合適的公比進行遍歷搜索,才能防止頻率的遺漏.相對頻率差一般取0.005<Δ ω< 0.04,過大或過小都會使陣發混沌現象消失,所以搜索時的公比也要取到該區間. 2)測定幅值之前也需要先進行預估,然后對待測信號放大或縮小,使幅值處于有效區間內,該區間由周期策動力頻率ω和待測信號頻率ω′決定,二者間相對頻差Δ ω越大,該區間也越大.幅值測定后,可以把測量結果從原信號中減去,判斷陣發混沌現象是否消失,若消失則證明結果正確. 3)由于系統狀態變化需要一定時間的激勵才能完成,導致相位的測量結果較實際值有不同程度的滯后,該滯后相位的大小主要由ω Δ ω決定,因此可以在測定頻率后通過仿真確定滯后相位的大小,加上測量結果,即得到較精確的相位值. 相較于混沌同步完成參數辨識的思想,本文的研究方法有以下優點: 1)速度快.一般在一個大周期后,如實例1,在t =11 s左右即可完成參數測定,而前者一般要40 s以上(見文獻[1]). 2)抗噪性好.一般可在信噪比達-100 dB以上的條件下檢出信號參數(見文獻[9]). 3)該方法能完整地測出待測信號的各項參數,這是目前前者所無法完成的,但在幅值和相位的測量精度方面還有待提高. [1]LüJ H,Lu J A 2003Chaos Soliton.Fract.17 127 [2]Zhou J,Lu J A,LüJ H 2006IEEE Transactions on Automatic Control51 652 [3]Wang X Y,Wu X J 2006Acta Phys.Sin55 605(in Chinese) [王興元、武相軍2006物理學報55 605] [4]Wang X Y,Wu X J 2008Int.J.M od.Phys.B 22 1015 [5]Wang X Y,Wang Y 2008Int.J.M od.Phys.B 22 2453 [6]Wang X Y,Li X G 2008Int.J.M od.Phys.B 22 4069 [7]LüL,Li Y,Guo Z A 2009Sci.Chin.Ser.G 39 77(in Chinese)[呂 翎、李 義、郭治安2009中國科學,G輯39 77] [8]Kim J H,Park C W,Kim E,Park M 2005Phys.Lett.A 334 295 [9]Hu J,ZhangQ J 2008Chin.Phys.B 17 503 [10]Ren H P,Han C Z,Liu D 2008Chin.Phys.B 17 1202 [11]Yang J G,Qu Z L,Hu G 1996Phys.Rev.E 53 4402 [12]Li Y,Yang B J,Shi Y W 2003Acta Phys.Sin.52 526(in Chinese)[李 月、楊寶俊、石要武2003物理學報52 526] [13]Li Y,YangB J,Lin H B,Liu X H 2005Acta Phys.Sin.54 1994(in Chinese)[李 月、楊寶俊、林紅波、劉曉華2005物理學報54 1994] [14]LiA,Wang S 2004Electr.Quality06 06(in Chinese)[李安、王 殊2004電子質量06 06] [15]Zhao X Y,Wei M X,Liu J H 2004Journal of Test and Measurement Technology18 16(in Chinese)[趙向陽、魏明獻、劉君華2004測試技術學報18 16] [16]Huang J C,Jing Z J 2007Chaos Soliton.Fract.40 1449 [17]Li S,Xu W,Li R H 2005Acta Phys.Sin.55 1049(in Chinese)[李 爽、徐 偉、李瑞紅2005物理學報55 1049] PACC:0545 Deter m ination of the parameters of unknown signals based on inter m ittent chaos* ZhaiDu-Qing?Liu Chong-Xin Liu Yao Xu Zhe (Institute of Electrical Engineering,Xi’an Jiaotong University,Xi’an 710049,China) 12 May 2009;revised manuscript 17 June 2009) We use the extreme frequency sensitivity ofDuffing’s equation to produce intermittent chaos(we call it“breather”) and propose a new method to quantitatively detect the parameters of unknown weak periodic signals.The theoretical analysis and instance simulation have proved its feasibility.We also put forward a way to improve the detection results and enhance the accuracy. Duffing’s equation,intermittent chaos,detecting the parameters of signals ?E-mail:zdq850831@sina.com ?E-mail:zdq850831@sina.com
3.利用陣發混沌現象測定待測信號參數
3.1.測定信號頻率
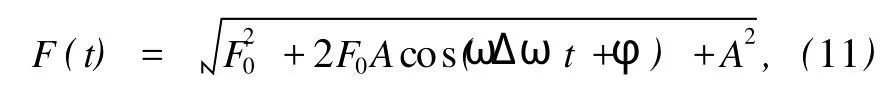
3.2.測定信號相位
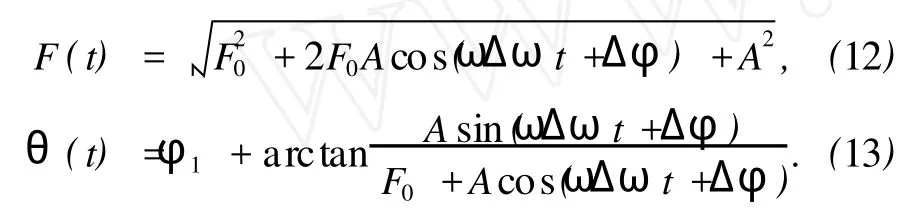

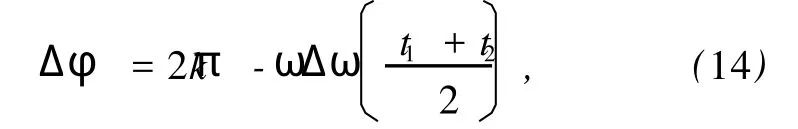
3.3.測定信號幅值
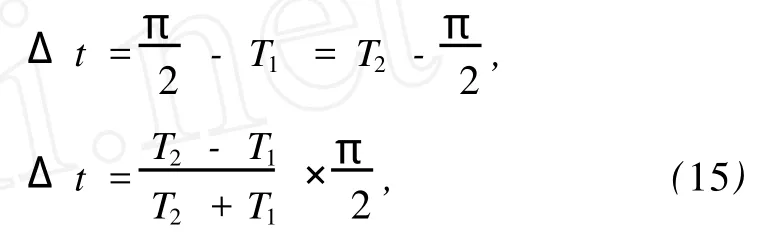
4.仿真實驗

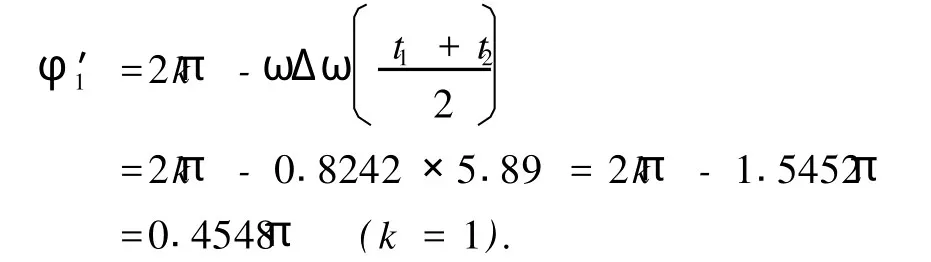


5.方法改進
5.1.相位測量的誤差分析及改進
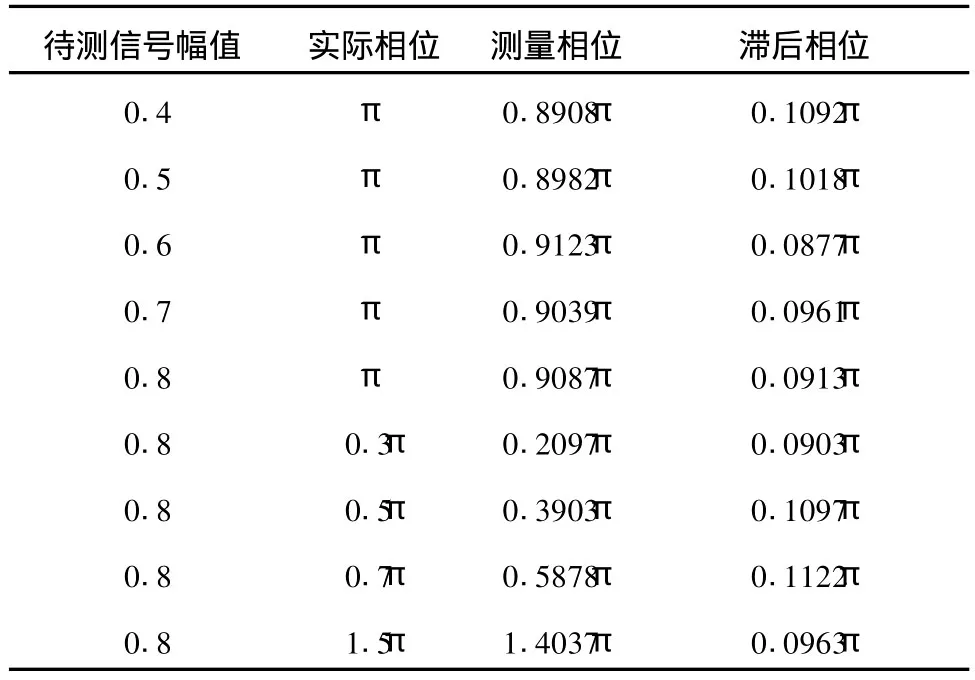
5.2.幅值測量方法的改進
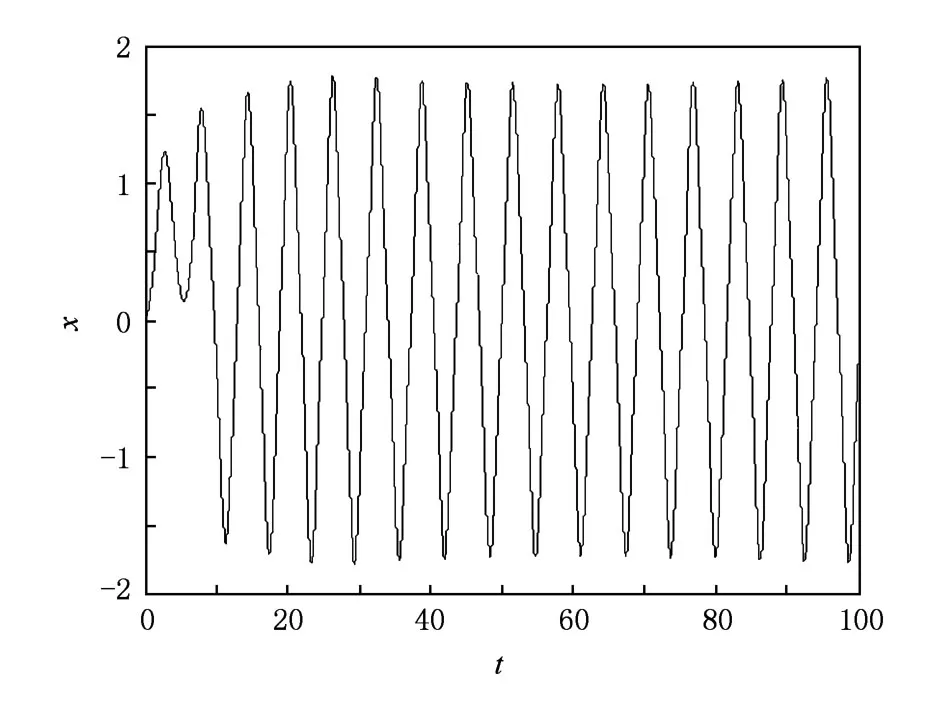
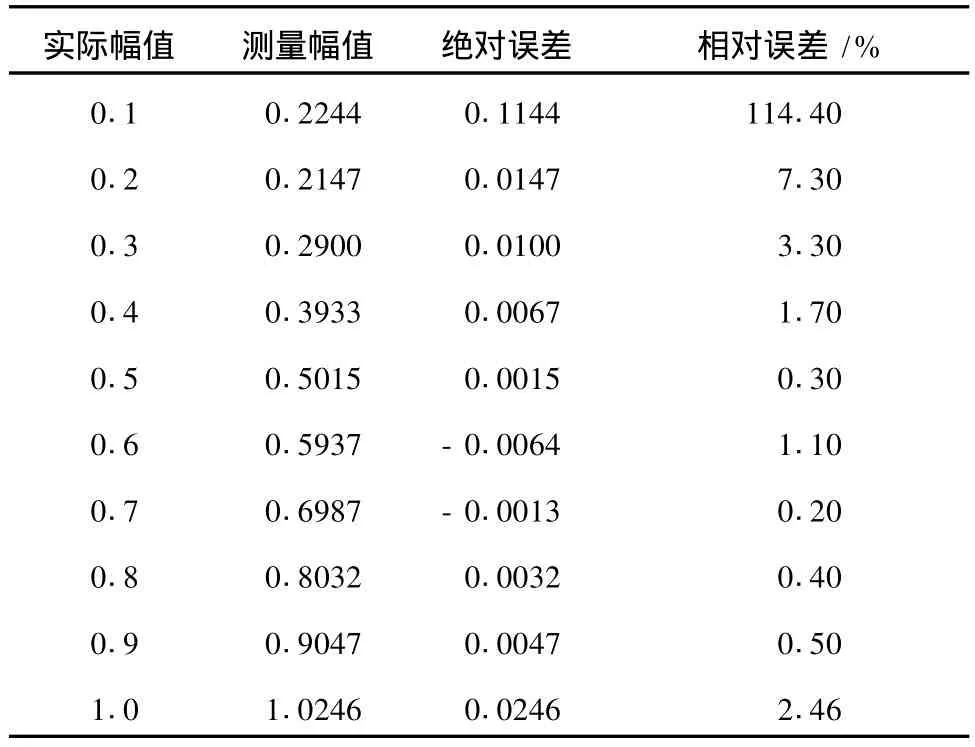
6.結 論

