Z+Z智能教育平臺在高中數學算法教學中的應用

張秀琦，張曉燕

（1渤海大學 教育學院，遼寧 錦州 121000；2河南省實驗中學，河南 鄭州 450002）

Z+Z智能教育平臺在高中數學算法教學中的應用

1張秀琦，2張曉燕

（1渤海大學 教育學院，遼寧 錦州 121000；2河南省實驗中學，河南 鄭州 450002）

在新課程標準中，算法已被列為高中數學的必修內容。本文對人教版高一數學必修3中算法章節部分進行了研究，對部分算法的效率進行了深入分析，并在Z+Z智能教育平臺上對改進后的算法進行了驗證。

Z+Z智能教育平臺；高中數學；算法

在普通高中數學課程標準中，算法模塊中要求學生通過模仿、操作、探索，學習設計程序框圖表達解決問題的過程；體會算法的基本思想以及算法的重要性和有效性，發展有條理的思考與表達的能力，提高邏輯思維能力[1]。

一、人教版高一數學必修3中兩個算法效率的分析

1．判斷質數算法

在1-1-1節中，教材中設計了一個算法，用來判斷一個數是否為質數。根據質數的定義：只能被1和自身整除的大于1的整數叫質數（教材第3頁附注），學生很容易接受書中提供的算法，即設這個數為n，用2～n-1這樣的數依次去除n，如果這些數都不能把n整除，則n為質數；否則n不是質數。

這個算法對于一般的數據都可以處理，而且現在計算機的速度非常快，計算的時間基本上可以忽略；但是在某些特定的問題中，等待我們去驗證的數往往比較大，在這種情況下，此算法的效率就要大打折扣了。以1011107例，若要驗證其是否質數，需用2～1011106去試，這樣判斷進行了100多萬次，按此算法編寫程序在QBASIC上從運行到出結果，明顯感覺有時間延遲。

其實在驗證的過程中，范圍可以縮小，由原來的[2，n-1]改為這個證明很容易：設p為n的一個因子，即p/n為整數，記為q，如果則一定有p∈[2，也就是說，如果在中不存在n的因子，那么在也不可能有 n的因子；故只需驗證這個范圍即可。

這樣的話，數1011107是否為質數，只需驗證大約1000多次即可，效率大大提高。

2．進制轉換算法

在1-3節的例4中，要求設計一個算法，把k進制數a（共有n位）化為十進制數b。其中算法第三步為：b=b+ai* ki-1，i=i+1。

在循環進行的n次中，每一次都要求一個ki-1，如果n比較小，這樣做無可厚非，但人們總是忍不住追求高效率，況且對于這個問題，提高效率并不難，只需稍稍改動一下算法，在算法中設w，用來表示ki-1，顯然，w每處理一位就要增長為w*k，修改后的算法如下：

第一步，輸入a，k和n的值；第二步，將b的值初始化為0，i的值初始化為1，w的值初始化為1，即k0；第三步，b=b+ai*w，i=i+1，w=w*k；第四步，判斷i＞n是否成立，若是則執行第五步；否則返回第三步；第五步，輸出b的值。

如果想進一步優化這個算法，還可以取消i，事實證明本算法中的i是完全可以省略掉的。亦可進一步延伸，讓學生比較針對同一問題所設計的不同算法的區別并體驗它，不但可以加深學生對算法設計重要性的認識，還可以讓學生對數學知識在算法設計中的靈活應用印象深刻。

二、Z+Z智能教育平臺下算法的驗證

由張景中院士主持開發的“Z+Z 智能教育平臺”適應我國數學課程改革的特點，充分發揮了信息技術條件下教學的優勢，可建立一個讓學生進行觀察、實驗、猜想、驗證的數學學習環境，讓學生親身經歷將實際問題抽象成數學模型并進行解釋與應用的過程[2]。該軟件可用于平面幾何、代數、解析幾何、立體幾何、概率統計、算法與編程、函數等中學數學課程的教學和學習。

學習算法，關鍵在于編寫出讓計算機執行的程序。看到計算機執行自己的程序并快速準確地給出問題的解答，會讓學生體會到學習算法的成就感；另一方面，若執行程序未得到自己預期的答案，則可以對自己的算法和程序進行檢查，通過實踐中的問題學習算法可以加深對算法及程序的認識和理解[3]。

人教版高一數學必修3中提供的算法程序是用BASIC語言編寫的，教師講授時大多在 QBASIC下運行程序，因此會出現上面提到的種種問題。相對于很多計算機高級程序設計語言來說，利用Z+Z智能教育平臺的程序工作區執行程序具有無須編譯直接執行命令并且即時得到運算結果的優點，也無須嵌入頭文件、各種類文件即可進行對應的運算，程序執行的速度較 QBASIC下快出很多，因此更適合在數學課上使用。以下給出改進后的兩個算法在Z+Z智能教育平臺下的程序及運行結果。其中圖1判斷質數程序執行后給出結果：1011107是質數，此改進后的算法在判斷1011107是否為質數時在該平臺下運行較改進前無時間延遲；圖 2進制轉換程序執行后給出二進制數 101轉換為十進制數為5。

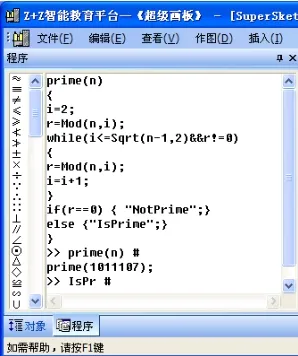
圖1 Z+Z下的判斷質數程序

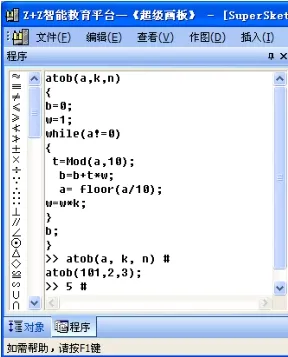
圖2 Z+Z下的進制轉換程序

三、總結

本文對人教版高一數學必修 3中算法章節部分進行了研究，對算法的效率進行了深入分析，給出了在Z+Z智能教育平臺上實現算法的程序，希望教師和學生能利用 Z+Z智能教育平臺豐富的功能提高對數學算法的認識和理解。

[1] 數學課程標準研制組．普通高中數學課程標準（實驗稿）[M]．北京師范大學出版社，2000．

[2] 張秀琦，唐吉洪，劉東芝．基于Z+Z智能教育平臺促進中學生數學知識建構與理解的研究[J]．湖北廣播電視大學學報，2010，（1）．

[3] 張景中．超級畫板自由行[M]．科學出版社，2006．

G434

A

1008-7427（2010）09-0146-01

2010-07-19

遼寧省教育科學“十一五”規劃2009年度一般課題《Z+Z 智能教育平臺在農村中學教學的應用研究》（課題編號JG09CB099）的研究成果。

作者張秀琦系渤海大學教育學院講師。