黃河流域水資源可再生能力評價的云模型3

賈 琦 段春青 陳曉楠

(1.武漢大學經濟與管理學院,湖北武漢430072;2.北京師范大學水科學研究院,北京100875;3.南水北調中線干線工程建設管理局,北京100038)

黃河流域水資源可再生能力評價的云模型3

賈 琦1段春青2陳曉楠3

(1.武漢大學經濟與管理學院,湖北武漢430072;2.北京師范大學水科學研究院,北京100875;3.南水北調中線干線工程建設管理局,北京100038)

對流域水資源可再生能力進行科學評判,針對評價中存在隨機性及模糊性的特征,建立起基于云理論的流域水資源可再生能力綜合評價模型。綜合考慮水資源條件、社會經濟條件及用水條件等11個指標建立水資源可再生能力評價指標體系,利用二元模糊對比法確定各個指標權重,借助云模型定量描述單指標條件下待評價區域水資源可再生能力的等級,并通過模糊變換,確定綜合評判等級。云模型將不確定性概念的模糊性和隨機性有機地結合在一起,用隸屬函數描述評價等級的模糊性,并利用超熵概念考慮隸屬度本身存在的隨機性,更符合實際評判的情況。應用該模型對黃河流域9個行政分區的水資源可再生能力進行了綜合評價,研究表明黃河流域的水資源可再生能力總體上較弱,其中寧夏和內蒙古最弱,其主要原因在于水資源總量短缺且水資源效率低,急需采取相關措施節流開源、提高產業用水效率,特別是需要進一步實施節水灌溉措施,降低農業灌溉定額,從而提高區域的水資源可再生能力。

水資源可再生能力;云模型;綜合評判

水資源可再生能力是指某一流域或區域水環境,在現有或近期科學技術和社會經濟能力支撐下,通過水自然循環與社會營造,循環利用水資源的能力[1]。區域水資源可再生能力的評價是該地區水資源開發利用決策的依據。黃河流經我國北方干旱,半干旱地區,是西北、華北地區重要水源。黃河流域地處我國半干旱、半濕潤地區,多年平均降水量在200-600 mm之間,屬資源性缺水區域。近年來,隨著區域國民經濟發展,黃河流域及沿黃地區生態環境建設,工農業生產和人民生活對黃河水資源的需求不斷增加,導致黃河水資源供求關系的全面緊張,生態環境惡化,20世紀70年代以來黃河斷流頻繁,黃河水資源可再生性面臨嚴重的挑戰。對黃河流域水資源可再生能力進行系統研究和科學評判是實現流域水資源可持續利用、實現當地社會經濟可持續發展的基礎。通過分析黃河流域及其所轄行政區域的水資源可再生能力大小,發現影響水資源可再生能力的制約因素,以便能夠及時采取相應措施,改善當地水資源情勢,研究具有重要的現實意義。此外,由于影響水資源可再生能力因素眾多,評價指標間關系復雜,各單項指標的評價結果往往不相容,因而水資源可再生能力的評價是多指標綜合評價問題。許多學者應用各種綜合評價方法對水資源可再生能力的評價進行了研究,如沈珍瑤利用灰色關聯分析方法與模糊綜合評判法對黃河流域水資源可再生能力進行了研究[2];楊曉華分別提出了水資源可再生能力綜合評價的遺傳投影尋蹤方法、遺傳加權物元模型等[3];陳守煜建立了基于可變模糊集理論的水資源可再生能力評價型[4]。模糊綜合評判相對完善成熟,但是隸屬函數一旦為精確數值表達后,就不在有絲毫模糊性了;投影尋蹤法需要結合某種非線性優化方法求解模型參數,計算較為復雜。特別地,這些傳統的評價方法在考慮評價指標的定量描述的不確定性、評價結果等級判定的不確定性時,未有考慮這些描述本身的不確定性,容易造成評價結果的不準確。本文針對上述不足,將定性與定量相互轉換的云模型引入水資源可再生能力研究中,將評價等級的模糊性和隨機性有機的結合在一起,以黃河流域為實例,實現區域水資源可再生能力的不確定性評價,研究具有理論意義。

1 云模型理論

1.1 云概念及其數字特征

云模型是我國李德毅院士提出的,是在傳統模糊數學和概率統計的基礎上建立起來的不確定性定性與定量互

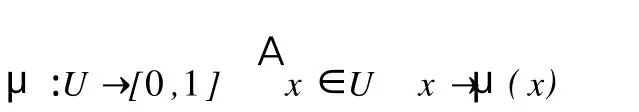
則x在論域U上的分布稱為云,每一個 x稱為一個云滴[7-8]。

從云的定義可以看出,云理論研究定性概念的量化方法。定性概念轉換成一個個定量值,是個離散的轉換過程,具有偶然性。每一個特定的點的選取是個隨機事件,可以用其概率分布函數描述。云滴的確定度反映了模糊性,這個值自身也是個隨機值,也可以用其概率分布函數描述。在論域空間中,大量云滴構成的云,可表征某一定性概念。

云用期望 Ex、熵 En和超熵He三個數字特征來整體表征一個概念。

期望 Ex:云滴在論域空間分布的期望。通俗地說,就是最能夠代表定性概念的點,或者說是這個概念量化的最典型樣本。

熵 En:定性概念的不確定性度量,由概念的隨機性和模糊性共同決定。一方面 En是定性概念隨機性的度量,反映了能夠代表這個定性概念的云滴的離散程度;另一方面又是定性概念亦此亦彼性的度量,反映了論域空間中可被概念接受的云滴的取值范圍。用同一個數字特征來反映隨機性和模糊性,也必然反映了它們之間的關聯性。

超熵 He:是熵的不確定性度量,即熵的熵。超熵用來度量云滴的隸屬度的隨機性,由熵的隨機性和模糊性共同決定。

1.2 基于正態云的定性與定量轉化模型

正態分布是概率理論中最重要的分布之一,通常用均值和方差兩個數字特征;鐘形隸屬函數是模糊集合中使用最多的隸屬函數。正態云模型是在二者基礎上發展起來的全新模型。正態云具有普適性,可以它為基礎進行定性概念的量化。

定義2 設U是一個用精確數值表示的定量論域,C是U上的定性概念。若定量值 x∈U,且 x是定性概念C的一次隨機實現,若 x滿足:x～N(Ex,En2),其中,En～N(En,He)2,且 x對C的確定度滿足換模型。它把不確定概念的模糊性和隨機性有機地結合在一起,實現了不確定語言值與定量數值之間自然轉化[5-6]。云的定義如下:

定義1 設 U是一個用精確數值表示的定量論域,C是U上的定性概念,若定量值 x∈u,且 x是定性概念C的一次隨機實現,x對C的確定度μ(x)∈[0,1]是有穩定傾向的隨機數

則 x在論域U上的分布稱為正態云。

一個定性概念可由正向正態云發生器產生,具體算法為:

(1)生成以 En為期望值,He2為方差的一個正態隨機數 En′i=NORM(En,He2);

(2)生成以 Ex為期望值,En′i2為方差的一個正態隨機數 xi=NORM(Ex,En′i2);

(4)具有確定度μi的xi成為數域中的一個云滴;

(5)重復步驟(1)到(4)n次,產生要求的 n個云滴。

所有的云滴組成了云,即為定性概念的表征。其中NORM為產生服從正態分布隨機數的函數。

通常在生成正態隨機數時,方差是不允許等于0的,因此在云發生器算法中通常要求 En和He都大于0。極端地說,如果 He=0,算法步驟(1)總是生成一個確定的值En,x就成為正態分布。更極端地說,如果 He=0,En=0,那么算法生成的 x就成為同一個精確值Ex,且μ恒等于1。從這個意義上說,確定性是不確定性的特例。

當某一定性概念經云模型量化后,即利用期望、熵和超熵三個數字特征來描述概念,此時如果給定論域 U1中的一個特定點 a,通過云發生器可以生成這個特定點 a屬于概念C1的確定度。這樣可以實現定量數值屬于某一定性概念的程度,具體方法如下:

(1)根據定性概念的數字特征熵 En和He超熵生成正態分布的隨機數 En′=NORM(En,He2);

2 基于云理論的綜合評判模型

本文以云理論為基礎,建立一種新的基于云的綜合評價模型。設因素集為 U={u1,u2,…,un},評價集為 V={v1,v2,…,vm},因素權重集 W={w1,w2,…,wn},它們均為有限集合。根據單因素的評價標準確定用云模型表示定性概念的數字特征,即(Ex,En,He)。設因素 i,i=1,2,…,n對應的等級j,j=1,2,…,m的上、下邊界值為 x1i,j,x2i,j,則因素 i對應的等級j這一定性概念可以用云模型表示,其中:

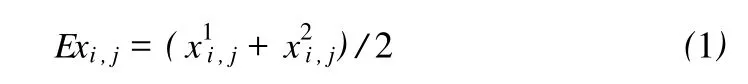
由于邊界值是從一種級別到另一種級別的過渡值,是一種模糊邊界,應同時屬于對應兩種級別,即兩種級別的隸屬度相等,因此有

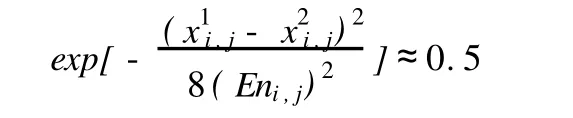
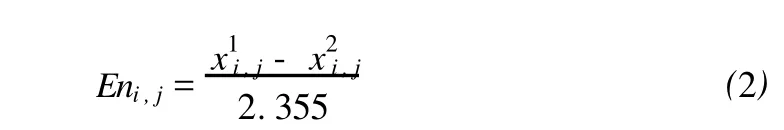
超熵 Hei,j表示對熵的不確定性度量,反映出云滴的凝聚程度,可以根據熵 Eni,j值的大小,通過經驗及試驗取值,超熵值越小,云的厚度越小,反之亦然。

確定出各個指標對應的每個等級的云模型數字特征后,就可以根據待評價項目的各個指標值,利用前件云發生器計算得出隸屬度矩陣 R

值得注意的是,由云模型得出的隸屬度矩陣不同于傳統模糊數學中的隸屬矩陣,它是隨機矩陣。隸屬度矩陣反映出了因素集U與評價集V存在的相關關系。權重集 W是因素集U上的模糊子集,利用權重集與隸屬度矩陣進行模糊轉換得出評價集V上的模糊子集B。

式中:B=(b1,b2,…,bm)表示評價項目隸屬于等級的程度;?代表一種運算。

傳統模糊數學方法多采用(×+)或(∧∨)運算,然后利用最大隸屬度原則進行決策。這種方法容易得出較為武斷的結果,不能反映事物本身界限的模糊性,損失的信息太多,有效度不高。特別是等級的隸屬度相等情況下,最大隸屬度原則會失效。因此,本文將利用模糊可變識別模型[9]計算綜合評判等級。具體計算如下列各式所示:

其中

式中,u′j為樣本關于級別j的非歸一化綜合相對隸屬度;p為距離參數,本文取 p=2;a為優化準則參數,本文取 a=1。則待評項目的等級可由下式計算:

式中:j3為評價的等級程度。

3 黃河流域水資源可再生能力評價

3.1 黃河流域水資源可再生能力評價指標體系

根據資料的可獲取性,綜合考慮各方面的因素,建立黃河流域水資源可再生能力研究指標體系以及制定評價標準[2]。表1和表2分別是水資源承載力評價指標及評價標準。

表1 水資源可再生能力評價指標體系Tab.1 Evaluation indicator systemof water resources reproducible ability

表2 水資源可再生能力評價指標標準Tab.2 Indexes for different water resources reproducible ability

各指標的權重利用二元比較模糊決策分析法獲得[9],如下所示:

(0.122,0.122,0.122,0.122,0.122,0.080,0.149,0.026,0.037,0.050,0.050)

黃河流域9個行政分區的指標值如表3所示:

3.2 黃河流域水資源可再生能力計算

根據建立的水資源可再生能力指標體系、評價指標標準,利用公式(1)-(2)將各個指標所對應的等級用相應的云模型表示,超熵取0.01,對于1級和5級這種邊緣級別采用半云模型,如第1個指標單位面積的水資源量,第5個等級范圍為0-0.05,則:

根據各個區域對應的指標值,利用正向發生器算法產生隸屬度矩陣,并利用(4)-(7)進行變換,計算得出不同區域的評價結果,如表4所示。

云模型與其它評價模型相比較,云模型的評價結果是隨機的,表4中的結果是一次隨機實現,但是其評價的結果必然在某一可接受的范圍內,如對青海水資源可再生能力的多次評價結果為3.52,3.52,3.45,3.47,3.46,這體現出了評價的不確定性;云評價與其他評判模型的評價結果相比較來看,評價結果大體上是其他方法評價結果的綜合,如對青海地區的評價,模糊可變集合、灰色關聯分析、模糊綜合評判結果為4級,而投影尋蹤評價結果為3.3級(近似3級),云模型評價結果為3.45-3.52,處于3-4級之間。對山西、陜西、全流域等的評價情況與對青海的評價情況類似,因此,綜合比較各種評價方法的評價結果,本文建立的云綜合評判模型是可行的。

根據評價的結果看出,黃河流域整體水資源可再生能力總體上較弱,屬3-4等級,主要原因為該區域本身屬水資源較短缺地區,目前區域內水資源總量不足,而且水資源的利用效率不高。特別是流域內的寧夏和內蒙古的水資源可再生能力最弱,屬4等級。從其指標值中可以看到寧夏和內蒙古的單位面積的水資源量極少,寧夏僅為01019m3/(m2.a),僅僅略高于山東省,在黃河流域所轄行政區中排倒數第二位,這是導致其水資源可再生能力弱的客觀因素,但是水資源的利用效率是影響水資源可再生能力的另一重要因素,與山東省相比,寧夏的萬元工業產值耗水率為5 499 m3/萬元,是黃河流域所轄行政區中用水效率最低的區域,山東省只有404 m3/萬元。綜上分析,黃河流域特別是寧夏和內蒙古地區急需采取相關措施提高目前水資源可再生能力,一是進一步節流、開源,合理實施跨流域調水,重視雨洪資源的利用,緩解水資源供需平衡的矛盾。二是急需提高用水效率,特別是降低提高農牧業的用水效率,大力推行節水灌溉,降低第一產業的灌溉定額,同時調整產業結構,降低耗水量。

表3 各區域指標值Tab.3 Indicator table of districts

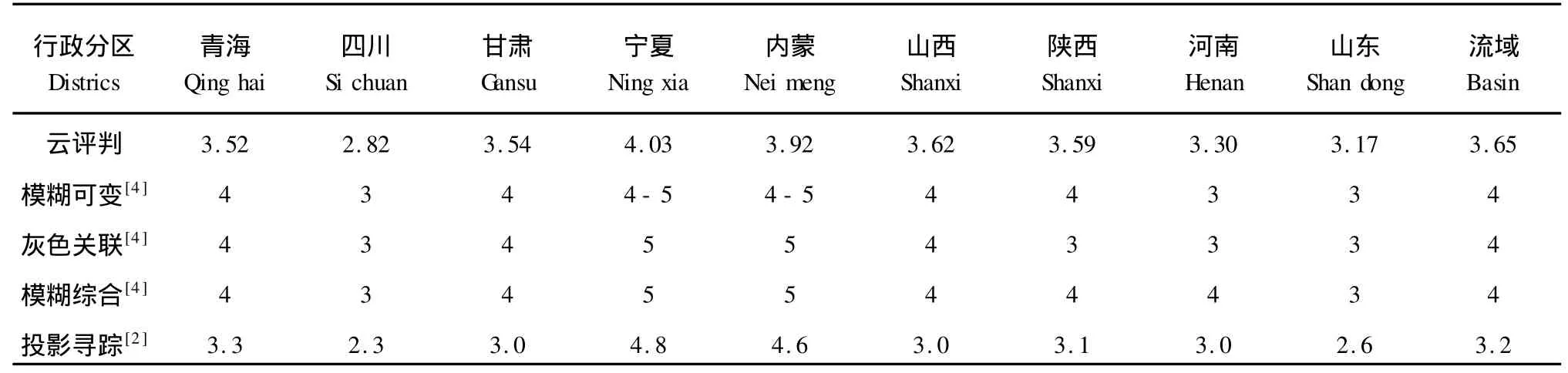
表4 不同區域的評價結果Tab.4 Evaluation results under different districts

4 結 論

本文在總結目前水資源再生能力評價方法的基礎上,將定性與定量轉化的云模型引入水資源可再生能力評價的研究中,并對黃河流域9個行政區水資源可再生能力進行評價,結果表明,黃河流域水資源可再生能力總體較弱。

云模型不僅考慮到概念的模糊性,而且充分考慮到評判的隨機性。將云綜合評判模型與傳統的模糊綜合評價、灰色關聯分析、投影尋蹤、模糊可變集合等方法進行了比較。評價結果表明,本文建立的綜合評價方法應用方便、結果可行。

References)

[1]沈珍瑤,楊志峰.黃河流域水資源可再生能力評價指標體系與評價方法[J].自然資源學報,2002,17(2):188-197.[Shen Zhenyao,Yang Zhifeng.Index System and Method for Assessing Water Resources Renew Ability of theYellow River Basin[J].Journal of Natural Resources,2002,17(2):188-197.]

[2]楊曉華,楊志峰,沈珍瑤,等.水資源可再生能力評價的遺傳投影尋蹤方法[J].水科學進展,2004,15(1):73-76.[Yang Xiaohua,Yang Zhifeng,Shen Zhenyao,et al.Genetic Projection Pursuit Method for Evaluating Water Resources Reproducible Ability[J].Advances in Water Science,2004,15(1):73-76.]

[3]楊曉華,楊志峰,沈珍瑤,等.水資源可再生能力綜合評價的遺傳加權物元模型[J].數學的實踐與認識,2004,15(1):73-76.[Yang Xiaohua,Yang Zhifeng,Shen Zhenyao,et al.A Genetic Matter Element Model with Weights for Comprehensive Assessment of Water Resources Producible Ability[J].Mathematics in Practice and Theory,2004,15(1):73-76.]

[4]陳守煜,李敏.基于可變模糊集理論的水資源可再生能力的評價模型[J].水利學報,2006,37(4):431-435.[Chen Shouyu,Li Min.Assessment Model of Water Resources Reproducible Ability Based on Variable Fuzzy Set Theory[J].Journal of Hydraulic Engineering,2006,37(4):431-435.]

[5]李德毅,邸凱昌,李德仁,等.用語言云模型挖掘關聯規則[J].軟件學報,2000,11(2):143-158.[Li Deyi,Di Kaichang,Li Deren,et al.Mining of Relation Rules with Cloud Model[J].Journal of Software,2000,11(2):143-158.]

[6]宋遠俊,楊孝宗,李德毅.多機多任務實時系統云調度策略[J].計算機學報,2000,23(10):1107-1113.[Song Yuanjun,Yang Xiaozong,Li Deyi.The Cloud Schedule Politics of Multiprocessor Multitask Real Time Systems[J].Chinese Journal of Computers,2000,23(10):1107-1113.]

[7]Li Deyi,HanJiawei,Shi Xuemei.Knowledge Representation and Discovery Based onLinguistic Atoms[J].Knowledge2based Systems,1998,15(10):431-440.

[8]Li Deyi.Knowledge Representation in K DD Based on Linguistic Atoms[J].Journal of Computer Science and Technology,1997,12(6):481-496.

Cloud Model of Water Resources Reproducible Ability in the Yellow River Basin

JIA Qi1DUAN Chun2qing2CHEN Xiao2nan3
(1.Wuhan University,Institute of Economy and Management,Wuhan Hubei 430072,China;2.College of Water Sciences,Beijing Normal University,Beijing 100875,China;3.Administration of the South2to2north Water Diversion Middle Route Project,Beijing 100038,China)

In order to evaluate water resources reproducible ability efficiently in region,a synthetic assessment model based on the cloud theory is suggested.The paper establishes assessment indexes system,calculates weights of indexes byfuzzy method,and describes evaluation grade of water resources reproducible ability under single indexfor each districts.The new evaluation model can not only show the fuzzyfeature of grade,but also indicate random attribute of the degree by hyper entropy.The paper applies the model into assessment of the water resources reproducible ability of 9 regions in the Yellow River Basin.Results show the water resources reproducible ability in the Yellow River basin is weaker,and the abilities in Ningxia and Inner Mongolia are the weakest.Some measures must be taken to improve the water resources reproducible ability in the Yellow River Basin.

water resources reproducible ability;cloud model;comprehensive evaluation method

TV213.4

A

1002-2104(2010)09-0048-05

10.3969/j.issn.1002-2104.2010.09.09

2010-04-04

賈琦,博士,高工,主要研究方向為調水企業管理、水資源管理。

3中國水利水電科學研究院開放基金 (No.IWHR02009002)項目資助。

(編輯:王愛萍)