運用切基線法測算卵形曲線要點解析
張家平,陳化新,于文勇
(1.黑龍江工程學院 土木工程系,黑龍江 哈爾濱 150050;2.哈爾濱市政研究院,黑龍江 哈爾濱 150001)
運用切基線法測算卵形曲線要點解析
張家平1,陳化新2,于文勇1
(1.黑龍江工程學院 土木工程系,黑龍江 哈爾濱 150050;2.哈爾濱市政研究院,黑龍江 哈爾濱 150001)
針對高等級公路復雜的卵形曲線測設與計算,將包含卵形曲線的整個平曲線分拆成非對稱基本型和特殊非對稱基本型兩種典型線形組合,同時,運用切基線原理和選定的設計參數,詳細解析第二圓曲線半徑的推算過程和方法,并給出具體應用要點和算例。
卵形曲線;切基線;圓曲線;緩和曲線
山區高等級公路以及互通式立交匝道經常會應用到卵形曲線,這種線形是公路平面線形設計與測設中難度較大的一種曲線,過去主要是應用雙交點法進行解算[1],但這種方法的缺點是,卵形曲線與雙交點基線并不相切,而是存在一個內移值,這對線位控制不是很準確。另外,雙交點法是一種近似的方法,精確解析比較困難,其原理是假設將中間的卵形曲線一分為二,前后交點各含一半長度。故僅能適用于低等級公路且緩和曲線長度較小時的情況,根本不能滿足高等級公路緩和曲線數百米長時的高精度要求。
本文給出一種運用切基線原理測算卵形曲線的新方法,可有效解決雙交點法的缺陷與不足,非常適合高等級公路以及高精度要求的長大卵形曲線的實際測設與計算,如圖1所示。
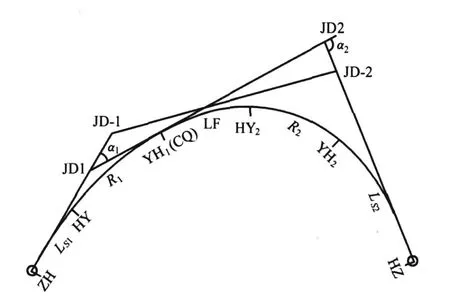
圖1 卵形曲線的兩種計算方法對比
1 切基線法測算卵形曲線的基本原理
如圖1所示卵形曲線,JD1、JD2處的轉角α1、α2以及切基線長度 S12為已知。假設 R1>R2,切基線剛好相切于 YH1,并可將整個平曲線拆分成兩個基本型平曲線,其中JD1控制的平曲線(ZH~YH1)是非對稱基本型(LS1—R1—0),JD2控制的平曲線(YH1~HZ)是特殊非對稱基本型(LF—R2—LS2),所謂特殊是指緩和曲線LF起點 YH 1的曲率半徑為 R1而非無窮大,即LF為曲率半徑由R1逐步減小到 R2的卵形曲線。
在計算原理和方法上,一般可先選定受限彎道,如JD1的曲線要素 R1、LS1,并算出切線長 T2;再試定JD2的曲線要素 LF及LS2,并根據切線長T3=S12-T2反算出第二圓曲線半徑 R2。
2 切基線法測設卵形曲線的解析計算

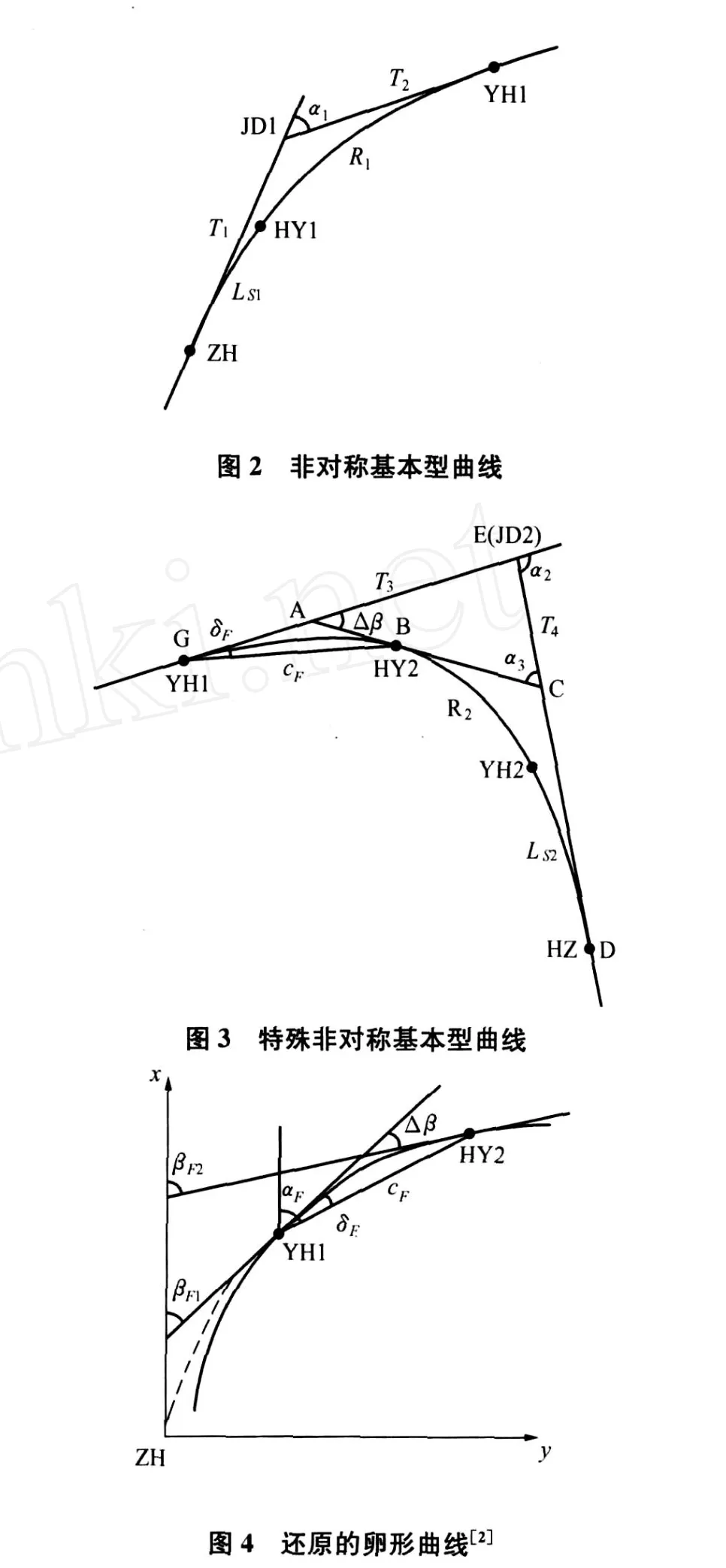


3 方法的應用

3. 2 計算模式的區分
本文計算方法是以R1 > R2 , 并根據已知條件R1 、L S1 、L F 、L S2 反算R2 為基本計算模式。對于由第二段曲線反算第一段曲線(已知R2 、L S2 、L F 、L S1 ,反求 R1),以及 R1<R2等情況,在計算原理和方法上是類同的,但須注意公式中各種參數的對應使用。
3.3 設計參數要求和檢驗
按《公路路線設計規范》的要求,在符合基本設計標準前提下(如最小半徑、最小線元長度),卵形曲線設計參數還宜滿足下面3個條件[5]:
1)R2/2≤AF≤R2(R2為小圓曲線半徑);
2)R2/R1=0.2~0.8;
3)D/R2=0.003~0.03(D為兩圓曲線間的最小間距)。
其中兩圓曲線間的最小距離 D可按下式計算[1]為
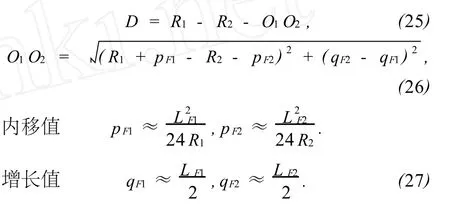
3.4 線位和參數控制建議
根據地形情況,可先在兩切線上初步擬定ZH和 YH1位置,根據切線長 T1、T2按式(1)和式(2)反算控制第一段曲線的設計要素 R1、LS1,若滿足設計標準要求,則可取整作為設計參數。
第二段曲線可按上一步關于卵形曲線設計參數的要求,選定 R2、LF,并由切線長 T3控制反算LS2,按此方法設計卵形曲線比較有利有效。
由于卵形曲線的約束條件多,需要反復試算、調整和檢驗才能達到滿意的設計結果,必要時甚至還可能需要結合地形條件改動JD1和JD2的位置。
4 算 例
某卵形曲線如圖 1 所示,已知α1=29°40′43″,α2=98°59′24″,兩交點距離 S12=732.561m。若擬定第一曲線的半徑 R1=1000m,緩和曲線長LS1=100m,中間的卵形曲線長度LF=140m,第二曲線的緩和曲線長LS1=100m,則第二曲線的半徑 R2及有關參數具體計算結果如表1所示。
5 結束語
本文探討運用切基線原理測算卵形曲線的解析方法,并給出詳細的推倒過程及算例,具有線位控制準確、可操作和應用性強的特點,特別適合于高等級公路和高精度計算要求的卵形曲線設計,若采用編程計算,則會取得更好的效果。

表1 切基線法解算卵形曲線結果
[1]張家平.卵形曲線測設與計算要點解析[J].黑龍江工程學院學報:自然科學版,2008,22(3):29-32.
[2]曲德福.公路卵形曲線任意點偏角計算與測設[J].東北測繪,2000,23(1):19-21.
[3]李裕林.淺談單卵形曲線的設計計算[J].四川建材,2008(3):4-7.
[4]初 東.公路卵型曲線測設新方法研究[J].西安工程學院學報,2001,23(3):71-75.
[5]交通部.JTG D20-2006公路路線設計規范[S].北京:人民交通出版社,2006.
[6]許婭婭,雒 應.測量學[M].北京:人民交通出版社,2003.
[7]楊少偉.道路勘測設計[M].北京:人民交通出版社,2006.
[8]劉 丹.緩和曲線精確計算的通用公式[J].廣西交通科技,2001,26(2):61-63.
Analysis to the key of setting out and calculation oval curve based on baseline of tangency
ZHANG Jia-ping1,CHEN Hua-xing2,YU Wen-yong1
(1.Dep t.of Civil Engineering,Heilongjiang Institute of Technology,Harbin 150050,China;2.Harbin M unicipal Institute,Harbin 150001,China)
The paper deals w ith the measuring and calculation of the comp licated oval curve of high classhighw ay,w hich is interp reted by full ho rizontal curve including the oval curve is divided up two typical alignment consisting of the dissymmetrical curve and special dissymmetrical curve,and the computational method and p rocess of the radiusof the second circle curve in detail based on the theo ry of tangent baseline and the selected design parameters,w hich is introduced by the key app lication point and the examp le.
oval curve;tangent baseline;circle curve;transition curve
U 412.3
A
1006-7949(2010)01-0017-04
2009-06-02
張家平(1964-),男,副教授.
[責任編輯李銘娜]

