雙饋風力發電機有功功率和無功功率的滑模解耦控制*

劉遠濤，楊俊華，謝景鳳，劉慧媛，吳 捷

(1.廣東工業大學自動化學院，廣東廣州 510006;2.華南理工大學電力學院，廣東廣州 510641)

0 引言

風能是一種隨機變化的過程性能源，為提高風能的利用率，通常采用變速恒頻發電方案，交流勵磁變速恒頻雙饋電機定子繞組直接接工頻電網，轉子繞組通過變頻器和電網相連，通過改變轉子側供電電源的頻率、幅值、相位及相序，能在較寬的轉速范圍內實現雙饋發電機的變速恒頻控制、最大風能捕獲控制、發電機輸出有功功率和無功功率的解耦控制。和轉子繞組相聯的功率變換器只需處理轉差功率，變換器的容量可大大減小。

雙饋風力發電系統中，發電機有功功率和無功功率的解耦控制是變速恒頻發電技術的難點和關鍵[1-2]。國內、外學者已經做了很多相關研究[1-6]，但大多數采用傳統的PI控制算法。文獻[3]在雙饋異步發電機(DFIG)有功與無功功率的解耦控制中應用了自抗擾控制策略;文獻[4-6]研究了傳統的比例積分(PI)雙閉環控制策略應用于DFIG有功與無功功率的解耦控制，外環為功率控制環，內環為電流控制環。但建模誤差及系統參數的攝動，給PI參數的整定帶來困難。現代控制理論同樣為控制實現提供了更多選擇。滑模變結構控制本質上是一種不連續的開關控制，它要求頻繁、快速地切換系統的控制狀態，具有快速響應、對系統參數變化不敏感、設計簡單、易于實現的特點，在風力發電系統中已有成功應用[7]。

在分析雙饋異步電機的動態數學模型和基于定子磁場定向矢量控制的基礎上，將滑模控制與比例積分控制相結合，給參數的整定帶來了較大方便，能有效實現雙饋風力發電系統有功功率和無功功率的解耦，提高了系統的動態響應和魯棒性。采用李雅普諾夫穩定性理論研究了系統的穩定性，建立了MATLAB/Simulink環境下系統的仿真模型，仿真研究結果驗證了控制策略的正確性和有效性。

1 基于定子磁場定向的雙饋發電機矢量控制

雙饋型風力發電機原理框圖如圖1所示。

圖1 雙饋型風力發電機基本原理

三相坐標系下雙饋發電機的數學模型是一個時變、非線性、強耦合系統，為實現發電機的有功功率、無功功率解耦控制，建立同步旋轉坐標系下的雙饋電機數學模型，采用了基于定子磁場定向的矢量控制技術。

1.1 雙饋發電機的數學模型

根據交流電機的動態分析理論，當定子側取發電機慣例時，轉子側取電動機慣例，雙饋發電機的數學模型表示如下[8]。

定子電壓方程為:

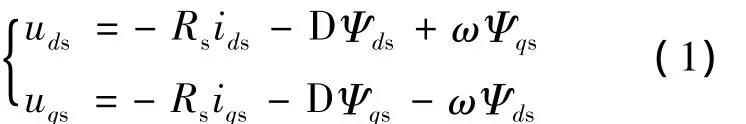
轉子電壓方程為:

定子磁鏈方程為:

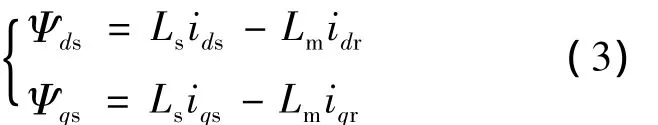
轉子磁鏈方程為:

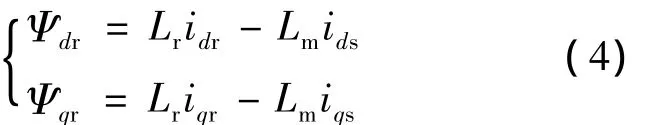
發電機定子側有功功率、無功功率方程為:

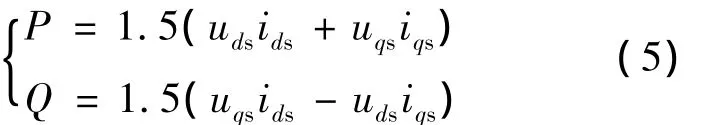
電磁轉矩方程為:

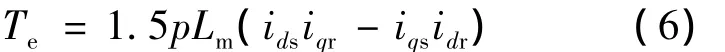
運動方程為:

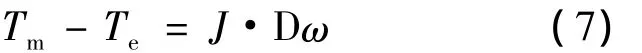
式中:uds，uqs，udr，uqr——分別為定、轉子 d、q 軸電壓;

ids，iqs，idr，iqr——分別為定、轉子 d、q 軸電流;

Ψds，Ψqs，Ψdr，Ψqr——分別為定、轉子 d、q 軸磁鏈;

Rs，Ls——分別為定子電阻和自感;

Rr，Lr——分別為轉子電阻和自感;

p——電機極對數;

Lm——定、轉子繞組間互感;

ω——同步角速度;

ωs——滑差角速度;

Tm——風力機作為原動機提供的驅動力矩;

J——轉動慣量;

D——微分算子。

1.2 基于定子磁場定向的矢量控制

基于定子磁場定向的矢量控制參考坐標系如圖2所示。

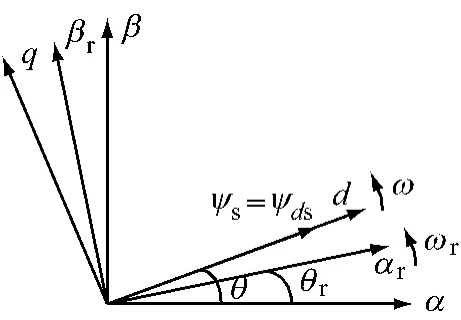
圖2 定子磁場定向矢量控制參考坐標系

將同步旋轉坐標系的d軸定向在定子磁場上，即取定子磁鏈Ψs方向與同步坐標系d軸重合，則定子磁鏈Ψs在d-q軸上的分量分別為:Ψds=Ψs，Ψqs=0。雙饋發電機正常運行時，定子繞組直接接電網，始終在工頻下運行，定子電阻壓降遠比電抗壓降和電機反電勢小，可以忽略電機定子繞組電阻[9]，定子磁鏈保持恒定。

基于同步坐標系下，方程式(1)定子電壓矢量轉換為:

由式(3)、(4)可得定子電流方程為:

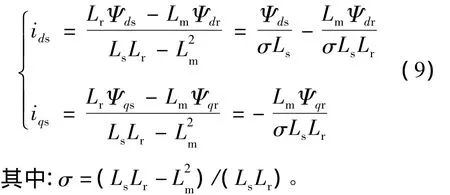
同步旋轉坐標系下，方程式(5)雙饋電機的瞬時有功功率、無功功率轉換為:

將式(8)、(9)代入式(10)，則有

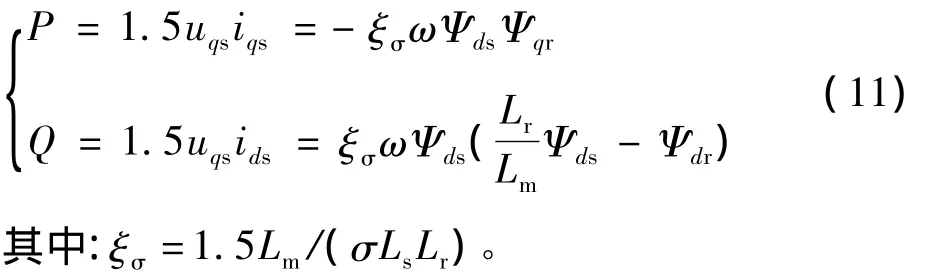
因為定子磁鏈Ψs恒定，由式(11)可得，在時間常量Ts內，有功功率、無功功率的變化量為:

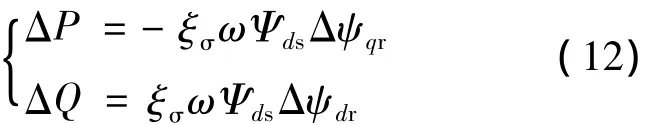
由圖2可知，滑差角速度ωs=ω－ωr。忽略轉子繞組壓降，在時間常量Ts內，調節轉子電壓來消除有功、無功功率誤差。基于同步旋轉坐標系，由式(2)、(11)、(12)可解得:

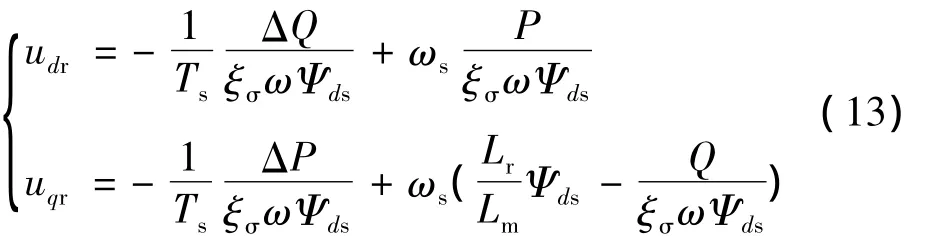
方程式(13)右邊第一項用來減小有功、無功功率誤差，第二項用來補償轉差引起的擾動。

2 滑模控制器設計

滑模變結構控制是變結構控制系統的一種控制策略，本質上是一種不連續的開關控制，它要求頻繁、快速地切換系統的控制狀態，具有快速響應、對系統參數變化不敏感、設計簡單、易于實現的特點。變結構控制系統的設計基于其運動特點及運行過程，通常分為兩個階段:能達階段和滑動階段。滑動模態是可以設計的[10]，且與系統的參數及擾動無關，處于滑模運動的系統具有很好的魯棒性。

2.1 滑模面s的選取

雙饋風力發電機滑模功率解耦控制方框圖如圖3所示。根據式(13)的關系，引入偏差變量，定義系統跟蹤誤差:

選取滑模面如下:

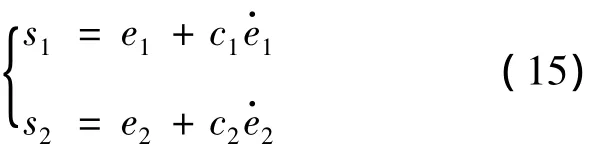
式中:c1、c2為滑模參數，選取適當的滑模參數，可使系統在滑模運動段有良好的動態品質[10]。

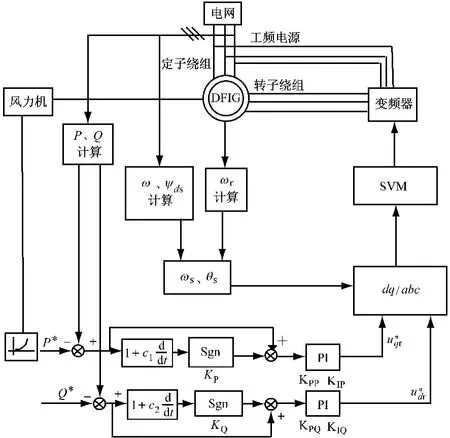
圖3 雙饋風力發電機滑模功率解耦控制框圖

2.2 滑模控制器的設計

令s1=0、s2=0，由控制器解得等效控制解，轉子繞組參考電壓:

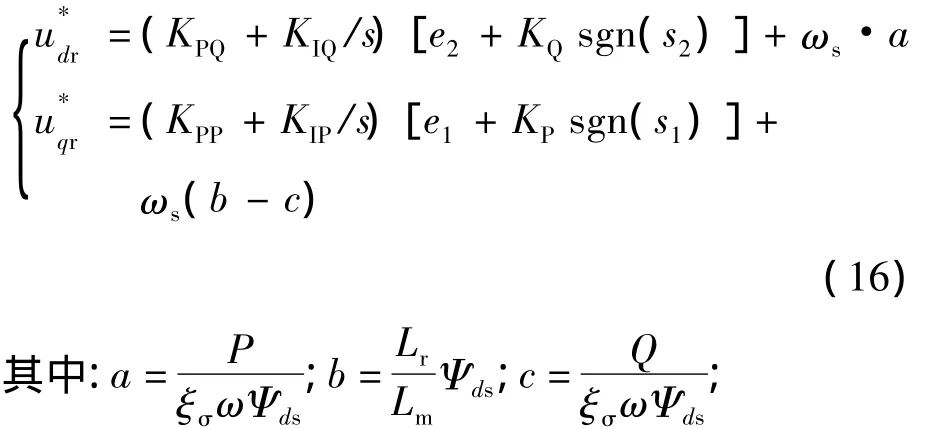
KPQ，KIQ——分別為無功功率 PI控制單元增益;

KPP，KIP——分別為有功功率PI控制單元增益;

KQ，KP——滑模控制單元增益。

聯立式(14)～(16)可以證明滑模運動的廣義存在條件式(20)成立，所以滑動模態存在。

在滑模運動段，功率控制器的輸入可以限制系統狀態在滑模面 s1、s2上。令 s1=0、s2=0，由方程式(15)解得:

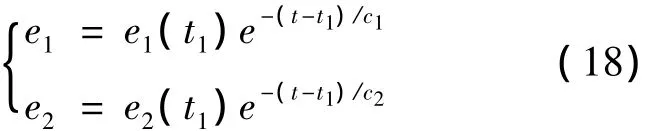
由式(18)可知，方程的解與雙饋電機參數和外部擾動無關，有利于PI控制單元的參數整定。主控制器包含一個滑模控制和一個PI控制單元。在暫態運行時，e1>KPsgn(s1)或e2>KQsgn(s2)時，PI控制單元起主要作用;在穩態運行時，系統跟蹤誤差很小，滑模控制單元起主要作用。在系統穩定范圍內，仿真研究表明，適當選擇控制單元的增益，可以很好地協調控制單元的控制效果。

2.3 滑模控制律的穩定性

對于能達階段，定義李雅普諾夫函數:

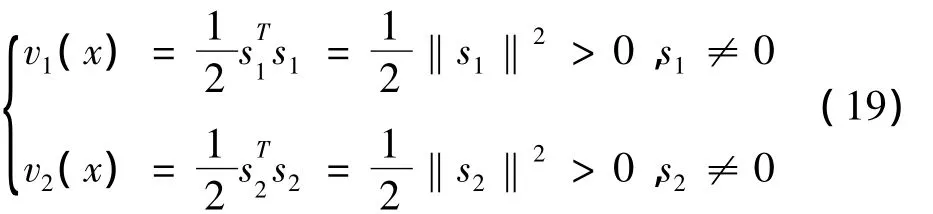
由式(22)可得:

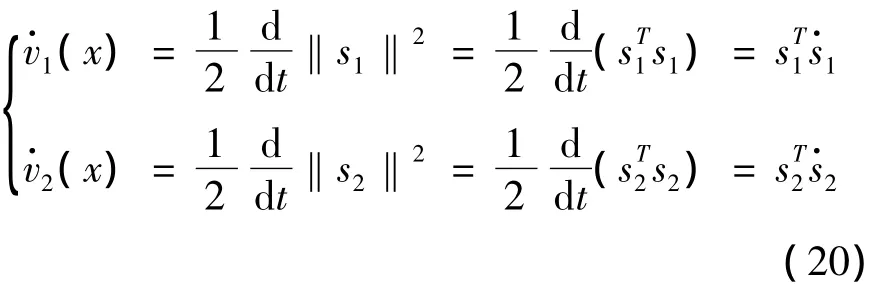
由式(14)～(17)可證明式(21)成立:

因此，滑模變結構控制系統在能達階段穩定，最終一定能到達滑動穩定域，即s1=0，s2=0。

3 系統仿真研究

基于MATLAB/Simulink平臺，建立了基于磁場定向的交流勵磁雙饋風力發電系統模型，對雙饋風力發電機系統有功功率、無功功率的滑模控制策略進行了分析和仿真驗證。DFIG參數為:額定功率2.5 kW，定子額定電壓380 V，頻率50 Hz;定子繞組電阻 Rs=1.9 Ω，定子繞組電感 Ls=0.25 H;轉子繞組電阻Rr=2.3 Ω，轉子繞組電感Lr=0.24 H;Lm=0.22 H。PI控制器增益:KPQ=0.3，KIQ=600，KPP=0.4，KIP=800;滑模控制器增益:KQ=1，KP=1.5，滑模參數:c1=0.000 1，c2=0.000 1。

仿真從穩態開始。圖4為雙饋風力發電系統無功功率給定調節過程，風速穩定在8 m/s，有功功率給定量P=1 kW不變。圖5為無功功率給定量在8 s時由0.6 kVA變為0.8 kVA，在9 s時由0.8 kVA變為0.6 kVA，雙饋風力發電系統有功功率P的響應曲線圖，此時系統有功功率變化非常小，基本不受影響。圖6為雙饋風力發電系統有功功率調節過程，給定風速改變，但無功功率給定量Q=0.6 kVA不變。圖7為t=13 s時，風速由8 m/s變為7 m/s;t=14 s時，風速由7 m/s變為8m/s，雙饋風力發電系統無功功率Q的響應曲線圖，此時有功功率P發生變化，由1 kW變為0.85 kW左右，而系統無功功率變化非常小，基本不受影響。

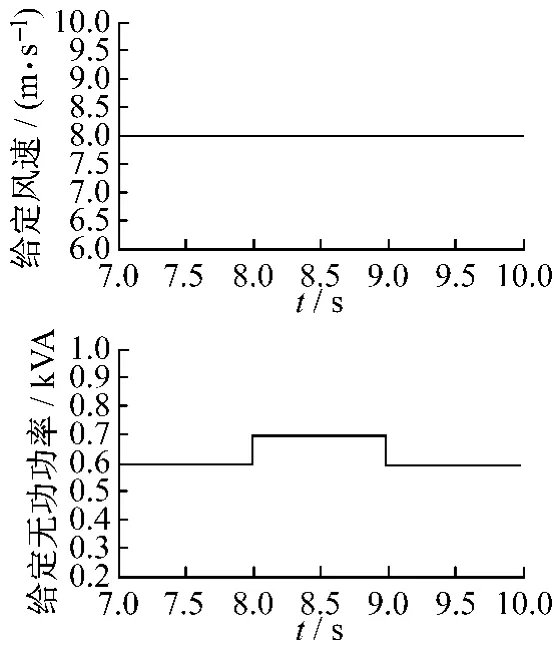
圖4 無功功率Q調節過程

圖5 DFIG有功功率P的響應

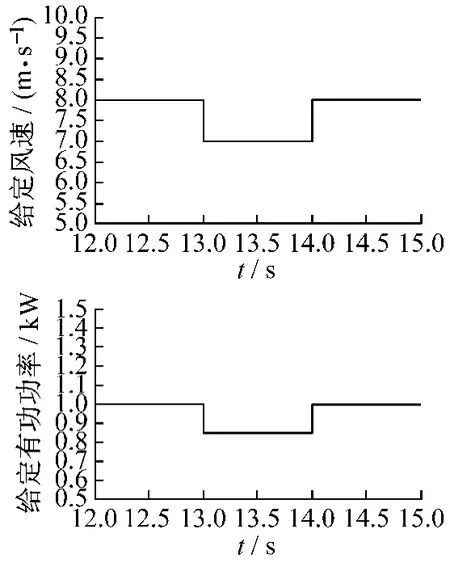
圖6 有功功率P調節過程

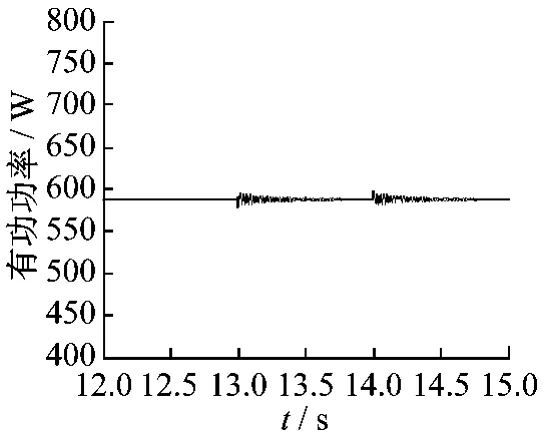
圖7 DFIG無功功率Q的響應

由以上分析可以得到:雙饋發電機的有功功率和無功功率實現了有效的解耦控制，充分驗證了該控制方案的正確性和可行性。

4 結語

在分析DFIG的動態數學模型和定子磁鏈定向矢量控制的基礎上，將滑模控制與比例積分控制相結合，得到一種有效的雙饋風力發電機功率解耦控制策略。應用李雅普諾夫穩定性理論分析了系統的穩定性，建立了MATLAB/Simulink環境下系統的仿真模型。仿真研究結果表明，該控制策略能夠有效地實現雙饋發電機有功功率和無功功率的解耦，而且功率解耦控制器具有較強的魯棒性。

[1]張琦瑋，蔡旭.最大風能捕獲風力發電系統及其仿真[J].電機與控制應用，2007，34(5):42-46.

[2]劉其輝，賀益康，趙仁德.變速恒頻風力發電最大風能追蹤控制[J].電力系統自動化，2003，27(20):62-67.

[3]張先勇，吳捷，楊金明.基于自抗擾解耦的變速恒頻風力發電功率控制系統[J].電氣傳動，2007，37(2):8-12.

[4]Pena Ruben，Cardenas Roberto.Control strategy of doubly fed induction generator for a wind diesel energy system[C]∥IEEE 28thAnnual Conference of the Industrial Electronics Society，2002，4(4):3297-3302.

[5]趙棟利，郭金東，許洪華.變速恒頻風力發電機有功、無功解耦控制研究與實現[J].太陽能學報，2006(2):174-179.

[6]黃守道，譚健，許錚，等.雙饋風力發電機有功、無功的解耦控制[J].電氣傳動，2008，38(9):7-10.

[7]Brice Beltran，Tarek Ahmed-Ali.Sliding mode power control of variable-speed wind energy conversion system[J].IEEE Trans Energy Conversion，2008，23(2):551-558.

[8]高景德，王祥珩，李發海.交流電機及其系統的分析[M].北京:清華大學出版社，1993.

[9]林成武，王鳳翔，姚興佳.變速恒頻雙饋風力發電機勵磁控制技術的研究[J].中國電機工程學報，2003，23(11):122-125.

[10]王豐堯.滑模變結構控制[M].北京:機械工業出版社，1998.