從著名的外森比克不等式引發的思考

● (咸陽師范學院基礎教育課程研究中心 陜西咸陽 712000)

1919年，數學家外森比克(Weitzenb?ck)提出了如下三角形邊長和面積的一個優美不等式：

問題1設△ABC的3條邊長為a,b,c，面積為Δ，則有不等式

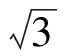
此題曾經作為1961年國際數學競賽題.圍繞不等式(1)有許多有趣的加強和拓廣.我們知道，早就有加強(1)的Tsintsifas不等式[1]：

問題2設△ABC的3條邊長為a,b,c，面積為Δ，則有不等式

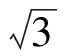
問題3設△ABC的3條邊長為a,b,c，面積為Δ，則有不等式

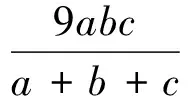
在文獻[2]中，作者將不等式(2)變形為：

問題4設△ABC的3條邊長為a,b,c，其半周長和面積分別為p,Δ，則有不等式

值得一提的是:1937年，數學家費恩斯列爾(Finsler)——哈德維格爾(Hadwiger)將不等式(1)加強為如下不等式：

問題5設△ABC的3條邊長為a,b,c，面積為Δ，則有不等式

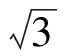
這個不等式還可以等價變形為：

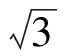
等價于

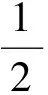
事實上，用不等式(3)來證明不等式(5)是非常簡單的，請看：

證明由三元均值不等式和不等式(3)，得

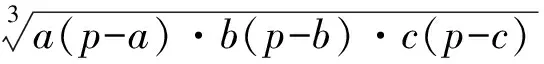
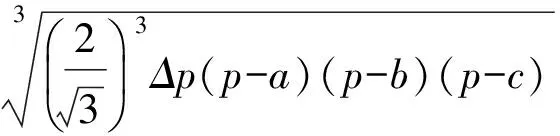
獲證.

早在1982年，重慶市第二十三中學高靈教師將不等式(4)推廣為2個三角形的情形：

問題6設△ABC和△A′B′C′的3條邊長分別為a，b，c;a′,b′,c′,其面積分別為Δ和Δ′，則有不等式

下面給出一個比較簡單的證法.

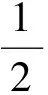
H2=[a′(b+c-a)+b′(c+a-b)+c′(a+b-c)][a(b′+c′-a′)+b(c′+a′-b′)+c(a′+b′-c′)]=

4[a′(p-a)+b′(p-b)+c′(p-c)][a(p′-a′)+b(p′-b′)+c(p′-c′)]≥

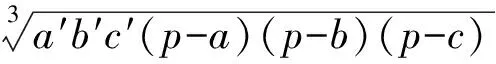
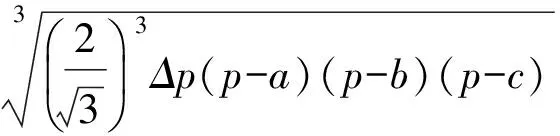
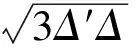
事實上，不等式(5)還可以推廣到多個三角形的情景(見文獻[2]).

問題7設△AiBiCi的邊長、半周長和面積分別為ai,bi,ci,pi,Δi(i=1,2,…,n)，則有

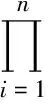
還需要指出的是，不等式(2)還可以繼續加強，得到如下的不等式：

問題8設△ABC的3條邊長為a,b,c，面積為Δ，則有不等式

證明由射影定理，得

a=bcosC+ccosB．

于是應用著名的柯西不等式，得

a2=(bcosC+ccosB)2≤(b2+c2)(cos2C+cos2B)，

即

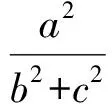
變形得

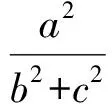
同理可得

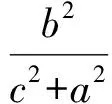
將這3個不等式2邊相加，便得

注意到常見的不等式

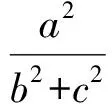
可得

再結合正弦定理，可得

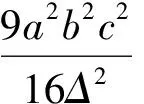
變形得

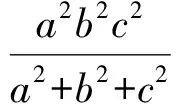
即

(本文獲咸陽師范學院重點科研課題(08XSYK110)、陜西省教育科學“十一五”規劃(SGH090228)項目支持.)

[1] 苗興振，董林.Weitzenb?ck及Tsintsifas不等式的加強[J].中學數學月刊，2010(2)：45.

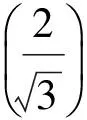
[3] 安振平.以三正數為邊長可構成三角形的充要條件及應用[J].湖南數學通訊，1985(3):17-19.