基于交通流灰色關聯熵的交通流無序轉化研究*

李 松 賀國光 張 杰

(河北大學管理學院1) 保定 071002) (天津大學系統工程研究所2) 天津 300072)

0 引 言

交通流無序是指處于交通擁堵狀態下的、通行能力很低的一種道路交通流,它實質是一種在時間、空間有序,而功能無序的道路交通流.交通流系統是復雜的開放巨系統,組成系統的各因素之間存在著復雜的非線性關系,它不僅能導致交通流混沌現象的產生,也會導致交通流無序的產生.近年來,交通流混沌的研究已經受到了交通流理論界的廣泛重視[1].關于交通流混沌的研究成果也越來越多[2-5].但是,對于交通流無序的研究卻是交通流理論研究的一個薄弱環節.交通流無序是交通流中很常見的一種交通流形態,是不能回避的一個交通流問題.為了能夠更好地對交通流實施控制,必須對交通流無序的轉化過程有一個較深入的認識.

本文是在目前交通流混沌研究的基礎上,通過跟馳模型模擬道路上發生交通堵塞事件產生的仿真交通流時間序列來研究了交通流無序的轉化過程;提出了交通流灰色關聯熵模型,并通過該轉化模型對交通流無序轉化過程作了分析.

1 基于跟馳模型的交通流無序轉化仿真

1.1 交通流無序仿真

仿真實驗選用改進的非線性跟馳模型[皮埃萊(Bierley)模型]來產生交通流的時間序列[6]

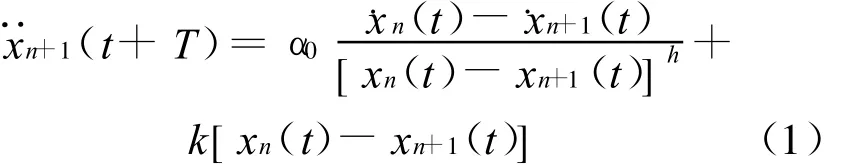
式中 :˙xn(t)為第 n 輛車(前車)速度;˙xn+1為第 n+1輛車(后車)的速度;α0為反應靈敏度系數,m/s;α0/[xn(t)-xn+1(t)]h為靈敏度的度量,其中h為常數;¨xn+1(t+T)為下一采樣時刻的n+1輛車的加速度;k為相對車頭間距的靈敏系數;xn(t)-xn+1(t)為車頭間距.

實驗中,假設頭車以速度V0勻速運動,取模型參數h=1、初始速度v0=15 m/s、初始車頭間距L0=15m;正弦干擾信號振幅 A=1m/s,角頻率ω=0.05 rad/s;同時,假設車輛在道路上行駛350 s時,突然發現前面出現交通堵塞事故,駕駛員會漸漸減速到v0=4m/s,而后勻速運動1 350 s之后,交通堵塞事故消除,駕駛員又提速到v0=15 m/s的速度,接著又以v0=15 m/s的速度勻速前行.針對不同的車輛數N、靈敏系數α0、車間距的靈敏度k產生不同的交通流序列,反復進行對比研究,從而得出該交通流模型在出現交通堵塞事故情況下產生交通流無序的規律.

圖1是當 N=5,(α0,k)組合分別為(8,0.000 08)、(14,0.000 08)、(16,0.000 005)、(5,0.000 008)時的車隊的第1～2輛車、第2～3輛車、第3～4輛車、第4～5輛車之間的車頭間距的時間序列,分別稱之為序列1、序列2、序列3、序列4.

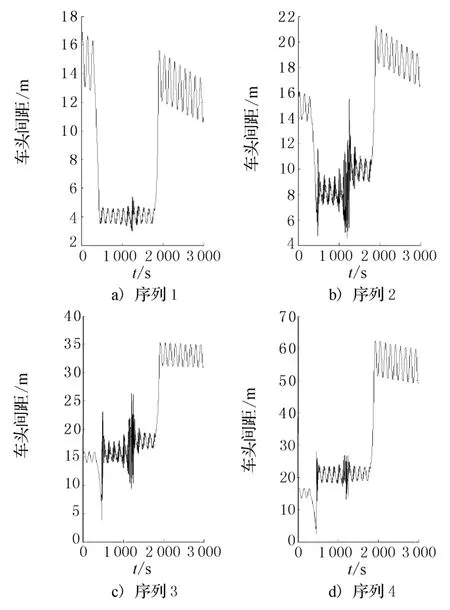
圖1 N=5時不同位置車輛的車頭間距時間序列

1.2 交通流無序運動特性分析

應用最大Lyapunov指數改進算法[7]計算仿真交通流時間序列的最大Lyapunov指數,結果列于表1.

表1 交通流時間序列的最大Lyapunov指數

從計算結果可以看出:5輛車之間不同的車頭間距時間序列的最大Lypunov指數均為正值,表明仿真交通流處于不可預測的無序狀態,存在交通流混沌.同時,序列 2和序列 3的 λ1要遠遠大于序列1和序列3的λ1.這說明不同位置的車輛之間的車頭間距時間序列的最大Lypunov指數λ1不同,其混沌程度也不相同.

交通系統無序是以一種特殊的交通流混沌方式體現出的喪失通行能力的功能無序.交通流無序在時間、空間上依然保持著有序,它體現的是一種宏觀無序而微觀有序的交通流狀態.因此,文中的交通流振蕩現象是一種交通無序現象.其特征是[8]:車輛行駛速度低于道路設計速度的30%、混沌持續時間較長,一般在20min以上,且一般其最大Lyapunov指數λ1＞0.1.

2 交通流有序運動與無序運動之間的轉化

2.1 交通流有序到交通流無序的轉化過程

由上述分析可以看出,在所設仿真條件下,仿真交通流產生了交通流無序現象.為進一步研究交通流從有序運動到無序運動的轉化過程,圖2和圖3分別給出了圖1b)在1～560 s時段的三維相圖和二維相圖.

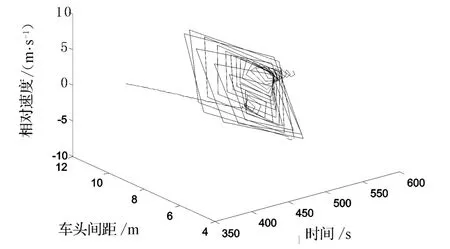
圖2 仿真交通流由有序向無序轉化三維相變圖

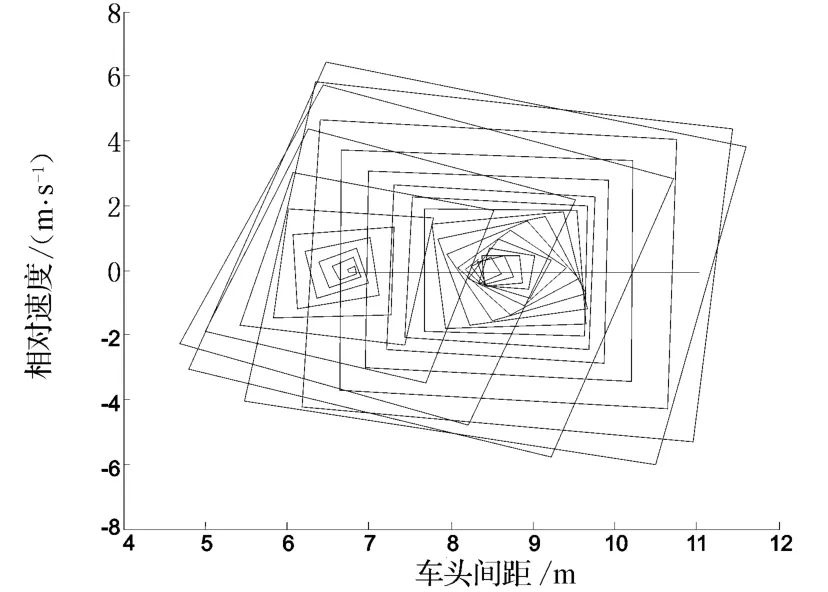
圖3 仿真交通流由有序向無序轉化二維相變圖

從圖2、圖3可以看出,仿真交通流從有序運動向無序運動轉化的初始階段具有交通流混沌的明顯特征(混沌吸引子在圖3中清晰可見).這說明在仿真交通流從有序運動轉化為無序運動的開始點——可以稱之為相變臨界點,是以有序運動向混沌運動轉化的方式實現有序運動向無序運動的轉化的,即在交通流有序向交通流無序轉化的過程中存在一種過渡狀態——交通流混沌.

實驗中發現,交通流有序運動向無序運動轉化以及交通流無序運動向有序運動轉化,都發生在交通流系統的非平衡相變臨界點附近,這個臨界點就是實驗中設定的交通堵塞事故的開始和結束.

2.2 交通流無序到交通流有序的轉化過程

由圖1b)和圖1c)可以看出,當仿真交通流從有序運動轉化為無序運動時,首先經過交通流混沌這樣一個轉化過渡狀態,然后轉化為混亂的交通流無序.這一階段交通流可能會在自組織的作用變得有一定的規律性,但其整體仍處于一個混亂(無序)的狀態.其后,由于交通流系統長時間處于無序狀態,駕駛員開始變得焦躁,使交通流陷于一個更大的混亂狀態,直至交通流再次變得相對規律些.如此反復,直到在非平衡相變臨界點交通流無序運動轉化為有序運動為止.

實驗發現,在交通流無序向交通流有序轉化過程中,會伴隨著一些交通流混沌現象的出現,并且能夠觀察到混沌吸引子的存在(相圖略).這也是交通流無序能夠反映出交通流混沌特性的一個原因.

實驗中還發現,在經過長時間的無序運動的交通流無序轉化為交通流有序時,交通流無序已經變得比較平穩.這一點,從交通流無序運動轉化為有序運動的相變圖看得更清楚,如圖4所示.由圖4可以看出,當交通流無序運動轉化為有序運動時,雖然車頭間距的變化仍然呈比較劇烈的震蕩狀態,但它已經變得相對有規律得多.

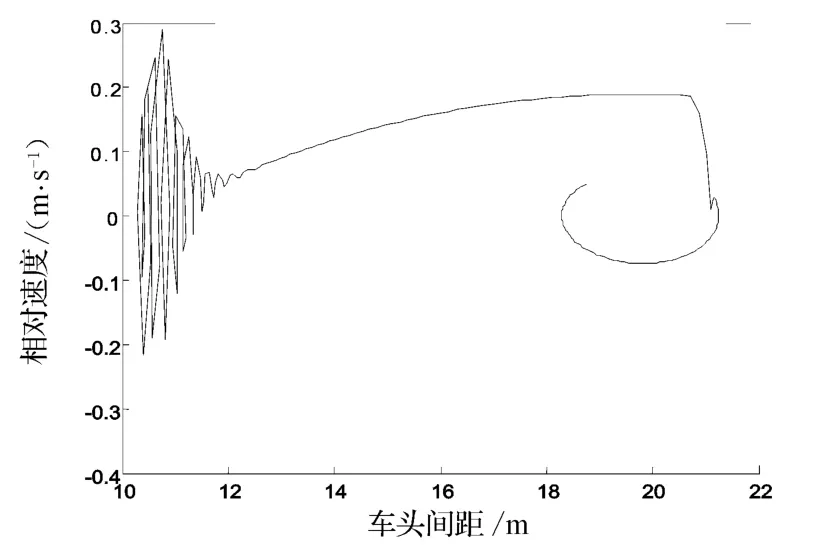
圖4 仿真交通流由無序向有序轉化相變圖

3 基于灰色關聯熵的交通流無序轉化分析

3.1 交通流灰色關聯系數

根據灰色系統理論[9],設

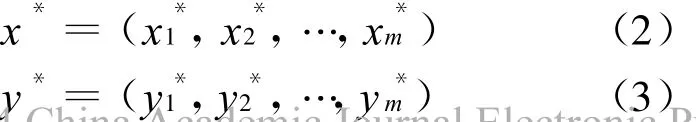
式中:xi*為某條路t時段的實際道路通行能力序列,xi*(1≤i≤≤m)為給定該條路中第i個路段的實際道路通行能力;yi*為保持道路暢通t時段該條路的最大允許道路通行能力序列;yi*(1≤i≤m)為給定該路第i個路段的最大允許道路通行能力.

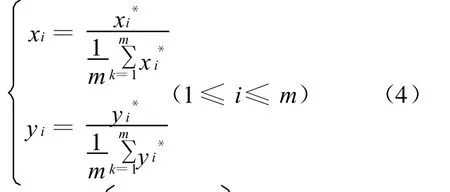
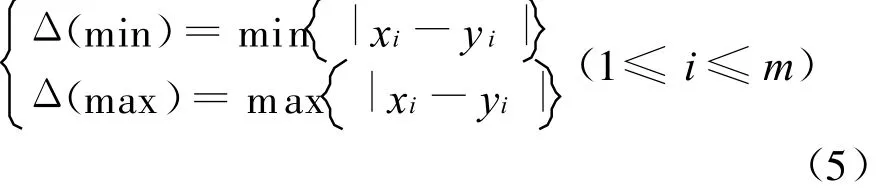
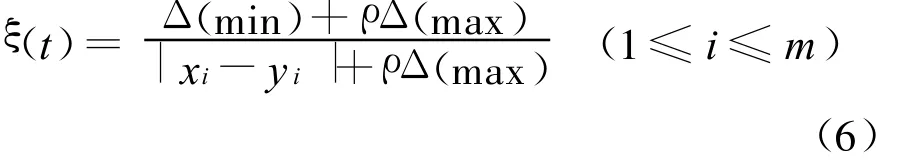
式中:ρ(0＜ρ＜1)為分辨系數,通過設置其值,可以控制ρΔ(max)對數據轉化的影響,一般取ρ=0.5時具有較高的分辨率.

3.2 交通流灰色關聯熵

按照信息熵的概念作如下定義.

定義1 設序列 X=(x1,x2,…,xn),xi≥0,且=1,xilog xi為X序列的灰熵,xi為屬性信息.

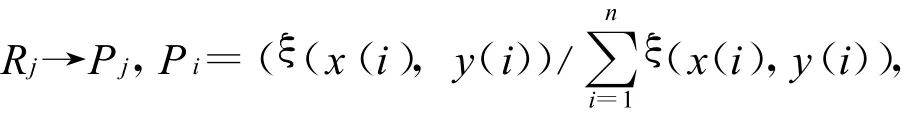
根據灰熵定義以及灰色關聯系數分布映射定義,交通流灰色關聯熵可以表示為

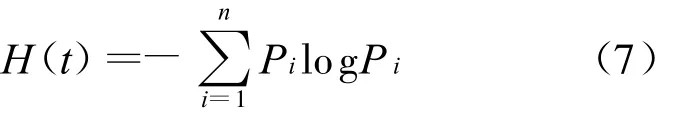
式中:H(t)為第t時段交通流系統的灰色關聯熵,是道路通行能力的狀態函數,當交通流系統狀態一定時,其交通流灰色關聯熵為確定值.

因此,交通流灰色關聯熵可以作為道路交通流無序的定量度量,即:H(t)=Pi log Pi≥0時,交通流處于有序狀態;H(t)=Pi log Pi＜0時,交通流處于無序狀態.

3.3 交通流無序的轉化分析

交通流系統是一耗散結構,其轉化方向取決于交通流系統運動機制,即取決于交通流系統熵變機制.因此,可以用熵理論和熵變關系作為檢驗和判斷交通流無序轉化規律的理論和方法.

式(7)僅考慮了交通流內部產生的灰色關聯熵,當考慮外界環境的信息交換時,交通流灰色關聯熵的完整表達式為

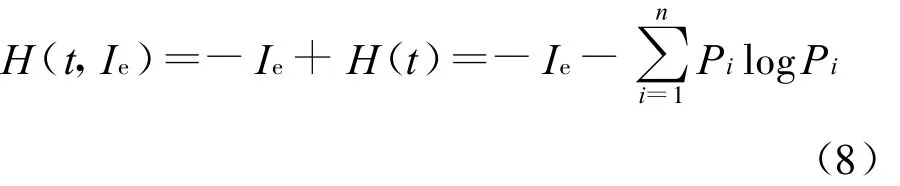
為此,建立交通流系統轉化方向的判別模型

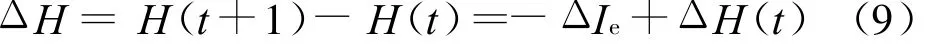
式中:ΔH為t時段系統與外界物能交換引起的熵變值;H(t+1)為系統第t時段的末態熵;H(t)為第t時段的初態熵;ΔI e=I e(t+1)-I e(t)為環境輸入的信息,即負熵流;ΔH(t)為系統不可逆交通流灰色關聯熵增加值,這個量總是正值.

根據交通流灰色關聯熵的熵變值ΔH的大小,可判斷交通流系統轉化方向和內部穩定程度:(1)當ΔH＞0時,交通流系統總熵增加,無序度加大,系統結構失穩,交通流系統處于不穩定狀態的惡性循環過程中,這時要通過某種措施加以調控.(2)當ΔH＜0時,即系統靠近熵產生最小的狀態,系統總熵減小,有序度增強,表明交通流系統處于良性循環狀態和過程之中,系統功能最佳.(3)當ΔH=0時,說明一定時間間隔內交通流灰色關聯熵的熵變值無變化,表明交通流系統狀態沒有變化.

因此,當 H(t)=- Pilog Pi≥0,即交通流處于無序狀態時,除了交通流的自組織及優化交通流序參量之外,還需要向交通流輸入外界信息,即負熵流,從而在一定程度上消減無序,幫助交通流實現有效的自組織,使其保持并恢復有序狀態.一般可將式(8)中I e的改變和控制稱為“交通流誘導管控策略”.此時,若要交通流無序轉化為交通流有序 ,則要:ΔI e＞0,且 ΔIe＞∣ΔH(t)∣,才有ΔH＜0,即在不違反熱力學第二定律的條件下,遠離平衡的非線性系統可以通過負熵流來減少總熵,從而使系統從無序態變為有序態.

反之,當交通流處于有序狀態時,即:H(t)＜0,此時,若 ,ΔIe＜0 且∣ΔIe∣≥∣ΔH(t)∣,則交通流有序就可能會轉化為交通流無序.

一個遠離熱平衡的開放系統要想從無序狀態轉變為有序狀態,就必須從外界獲得信息(負熵).這是自組織理論導出的基本結論.所以,在實際交通流中,除了交通流序參量的優化之外,還需要向交通流輸入外界信息,即負熵流,從而在一定程度上消減無序,幫助交通流實現有效的自組織,使其保持并恢復有序狀態.

4 結 束 語

本文利用跟馳模型產生的仿真交通流研究了交通流有序運動與無序運動之間的轉化過程;提出了基于交通流灰色關聯熵的交通流無序轉化模型,并通過該模型對交通流無序轉化過程作了分析.從仿真結果及其分析可以得出如下結論:交通流無序是一種復雜的交通流狀態,其轉化過程是復雜多變的,且轉化過程中存在交通流混沌現象;交通流系統要從無序運動轉化為有序運動必須要從外界獲得負熵流——信息熵.

[1]王東山,賀國光.交通流混沌研究綜述[J].土木工程學報,2003(1):68-73.

[2]Low D J,Addisonp S.Chaos in car-fo llowingmodel w ith a desired headw ay time[C].Proceeding of the 30thISATA Conference,Florence,Italy,1997,175-182.

[3]馮蔚東.基于自組織理論的交通流及其管控研究[D].天津:天津大學系統工程研究所,1998.

[4]張智勇,榮 建,任福田.跟馳車隊中的混沌現象研究[J].土木工程學報,2001(1):58-59.

[5]賀國光,萬興義,王東山.基于跟馳模型的交通流混沌研究[J].系統工程,2003(2):50-55.

[6]丹尼爾·L·鳩洛夫,馬休·J·休伯.交通流理論[M].蔣 璜,譯.北京:人民交通出版社,1983.

[7]李 松,賀國光.基于最大Lyapunov指數改進算法的交通流混沌判別[J].武漢理工大學學報:交通科學與工程版,2006,30(5):747-750.

[8]李 松,賀國光,張曉利.一種基于交通熵的交通流無序度量方法[J].公路交通科技,2007(11):92-95.

[9]鄧聚龍.灰色系統理論教程[M].武漢:華中理工大學出版社,1990.