復雜柔性車載液壓機械手彈性動力學建模方法研究

馬振書 梅 濤

1.中國科學院合肥智能機械研究所,合肥,230031 2.中國科學技術大學,合肥,230026

3.軍械技術研究所,石家莊,050000

0 引言

車載機械手用于在遠距離遙控中對危險品彈藥進行抓取和搬運,并且在將炮彈放置到安全地點前保證其不會爆破,以避免造成人員傷亡。由于路面情況復雜,機械手在行走過程中極易由于彈性振動而使炮彈自行爆破,因此機械手的振動控制是保證其可靠工作的關鍵所在。動力學建模是實現機械手動態設計和振動控制的理論基礎。在柔性機械手動力學建模方面,Agrawal等[1]、Sunada等[2]利用有限元法將剛彈耦合引入到柔性機械手動力學模型中,建立了機械手的控制方程;崔玲麗等[3]利用有限差分法和有限元法建立了單桿柔性機械臂的動力學模型,模型中包含了機械臂的形狀參數以及驅動器的參數。但對于多連桿柔性機械手而言,采用有限元法的動力學建模限制了計算速度的提高,使之成為機械手控制實現的一大障礙。王樹新等[4]利用有限線段法建立柔性機械臂的離散模型,以基于Kane方程的Huston方法建立柔性機械臂的動力學方程,該方程中計入了幾何非線性變形的慣性影響,包括非對稱截面當量彈性力對于廣義主動力的貢獻。Johanni[5]、李光等[6]利用假設模態法建立了形式簡捷的動力學方程。曹學民等[7]利用多體系統理論建立了柔性機械手的動力學普遍方程,綜合考慮了剛彎、剛扭和彎扭耦合的影響。

考慮所研究的車載機械手實際結構的復雜性[8-12],筆者在綜合考慮動力學控制實現的基礎上,借助固定界面模態綜合法研究這類車載機械手彈性動力學建模方法,并在子結構劃分中有效地利用約束模態坐標建立了機械手本體與液壓作動器之間的聯系。探討了結構參數對系統低階模態的影響規律,以期為這類機械手的動態設計和振動控制提供理論依據。

1 系統簡介與基本假設

本文所研究的車載機械手如圖1所示,由搖桿OB、伸縮桿套CE和由絲杠螺母驅動的伸縮桿GC、手爪控制桿GH和HE組成,該機械手由2個液壓缸和2個伺服電機驅動,實現機械手的位姿調整。在彈性動力學建模中假設各轉動副為理想約束。

根據機械手各彈性桿件之間的連接關系、約束條件及建立的振動控制模型,可將機械手視為

2 動力學建模

根據搖桿、伸縮桿套和伸縮桿、手爪控制桿相互之間的連接關系和邊界約束條件,將搖桿OB視為2個鉸支固支梁,以模擬搖桿與安裝車體、搖桿與伸縮桿套間的轉動副連接,而搖桿與液壓作動器的連接處用固支處理;伸縮桿套CE視為兩個固支梁和一個懸臂梁,伸縮桿視為一個固支梁和一個鉸支固支梁,手爪控制桿視為兩個鉸支梁,鉸支端分別模擬伸縮桿和手爪控制桿間的轉動副連接。從而,機械手可視為9個子結構的組成,利用固定界面模態綜合法構造機械手的彈性動力學模型。

2.1 子結構模態基的構造

設桿件是密度為 ρ、截面積為 A、桿長為 l、抗彎截面模量為EJ的等截面細長均質桿。為方便書寫和計算,暫略去連桿下標,且在梁的一端的截面中心建立局部坐標系Oxy,使得軸 x的方向與連桿的軸線重合,如圖2所示。將桿視為歐拉梁,則其在坐標系Oxy下,沿y軸的彎曲振動方程及x軸的縱振控制方程可表示為

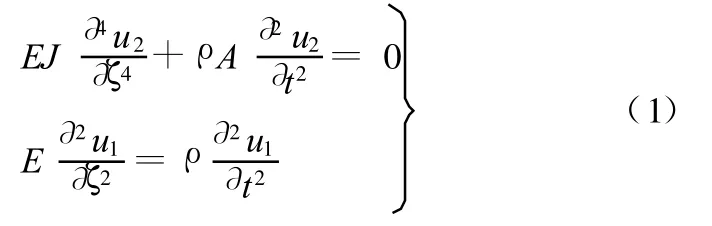
考慮外部激勵,則式(1)可寫為

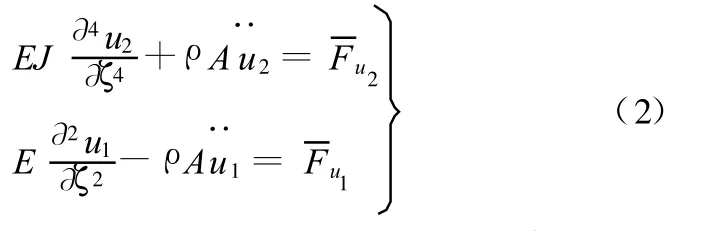
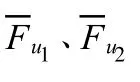
考慮到系統旋轉副為理想約束,故利用固定界面法可極為方便地構造出鉸支固支梁的彎曲振動主模態和縱向振動主模態,即若干個不同支承條件的彈性梁組合,如圖2所示。

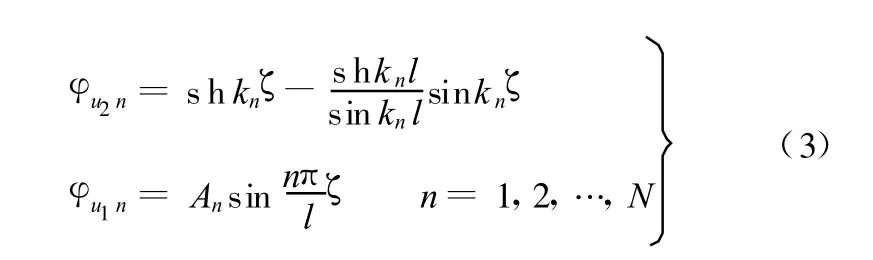
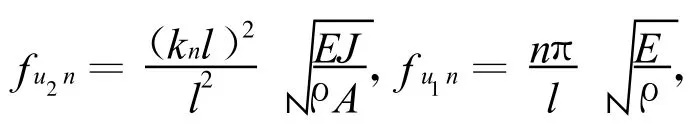
圖3所示為子結構約束坐標定義。將鉸支固支梁兩端的移動自由度和固支端的轉動自由度作為約束自由度(圖 3a),可構造出界面約束模態函數:

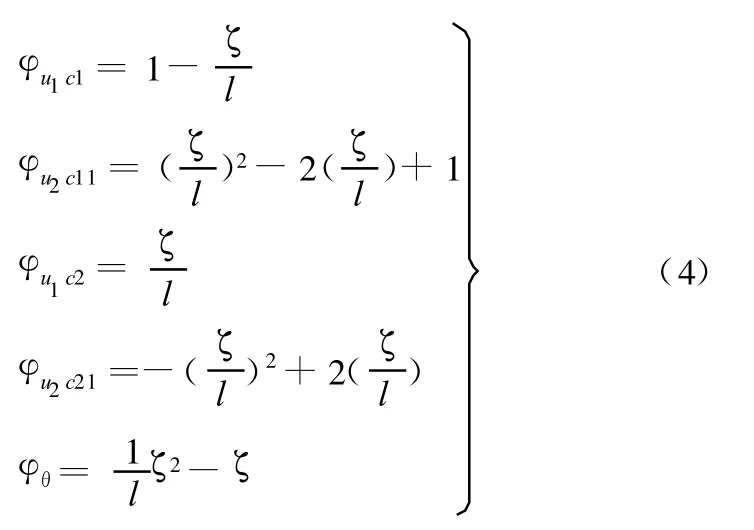
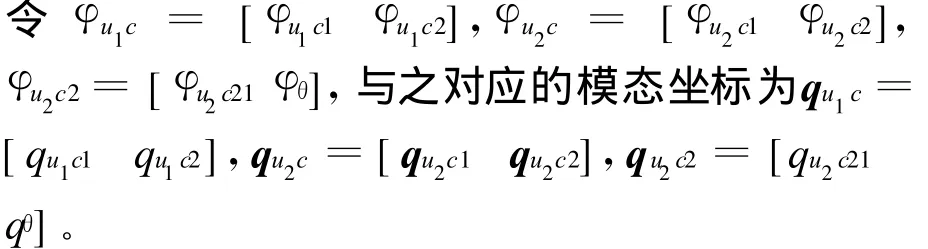
改變鉸支端的約束條件為固支,同理可構造出固支梁的彎曲振動主模態和縱向振動主模態,即

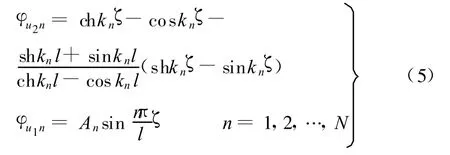
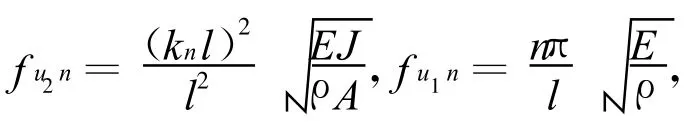
將固支梁兩端的移動和轉動自由度作為約束自由度(圖3b),亦可構造出固支梁的約束模態函數:

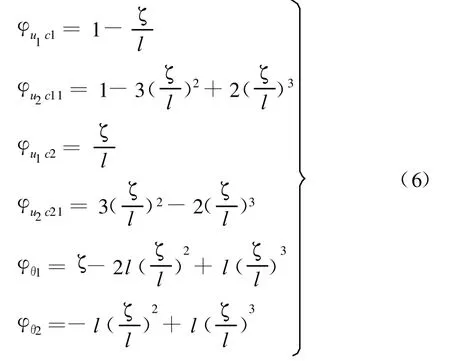
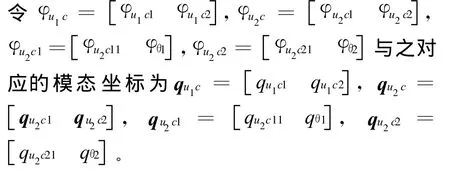
釋放固支梁的一端,就可得到懸臂梁的彎曲振動主模態和縱向振動主摸態:

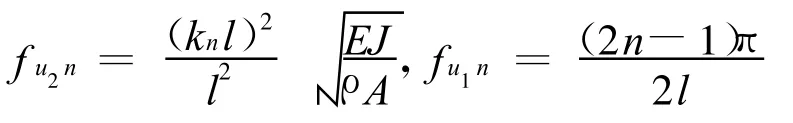
將懸臂梁的邊界移動和轉動自由度作為約束自由度(圖 3c),可構造出懸臂梁的約束模態函數:

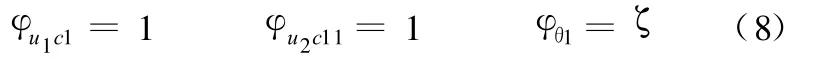
將鉸支固支梁的固支端改為鉸支,可構造出鉸支梁的彎曲和縱向振動主模態:

將鉸支梁兩端的移動自由度視為約束自由度(圖3d),可得到鉸支梁的約束模態函數:

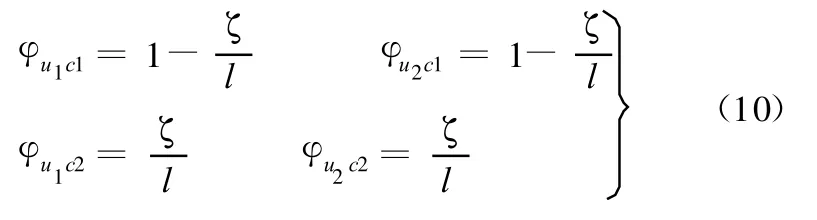
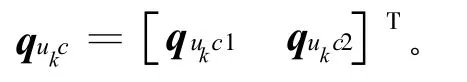
2.2 子結構的動力學模型

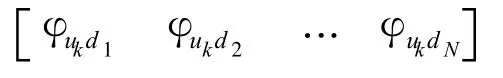
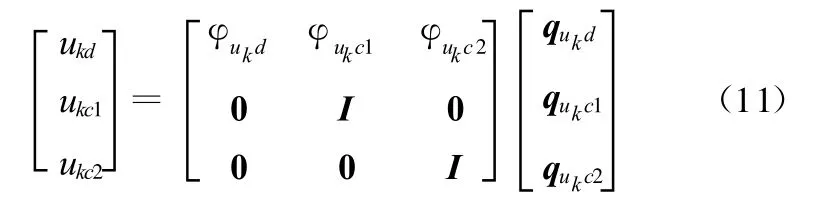
將式(11)代入式(2)可得到uk方向模態坐標下的振動微分方程

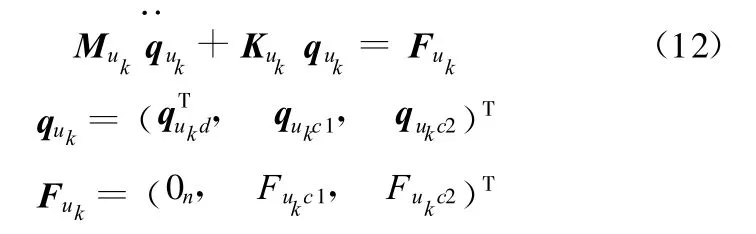
式中,quk、Fuk分別為廣義坐標和廣義力列陣,其中Fukc1=Fukc1w+Fukc1n,Fukc2=Fukc2w+Fukc2n;Fukc1為uk方向上各子結構對接的邊界力和作用在邊界上的外部激振力的組合;Fukc1w、Fukc2w為外部激振力;Fukc1n、Fukc2n為對接的邊界力;Muk、Kuk為該方向的主質量和主剛度矩陣。

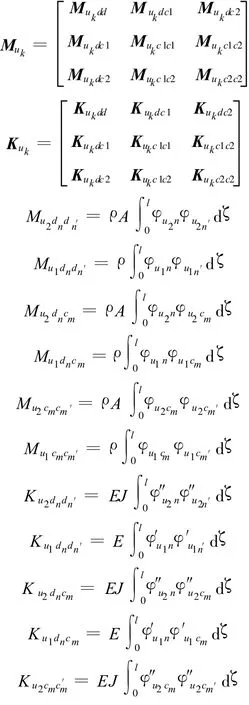
則單個子結構的振動方程為

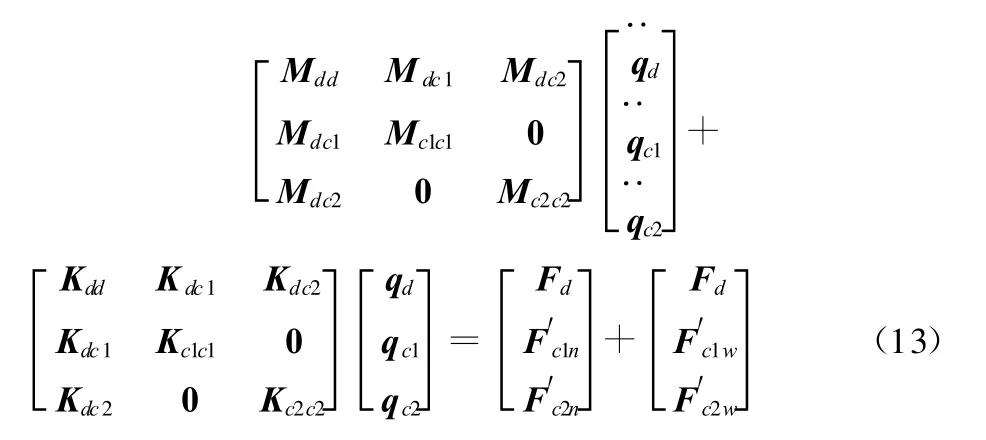
2.3 柔性車載機械手的彈性動力學模型

如圖2所示,子結構(1)和(2)可視為鉸支固支梁,二者在A點的變形協調條件可表示為

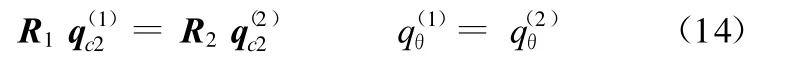
式中,Ri為子結構i的局部坐標系的方向余弦矩陣。

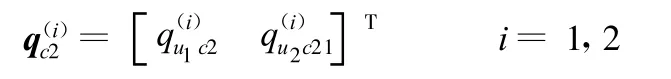
子結構(3)和(4)可視為固支梁,二者與子結構(2)在B點的變形協調條件可表示為

子結構(5)可視為懸臂梁,其與子結構(4)在D點的變形協調條件可表示為

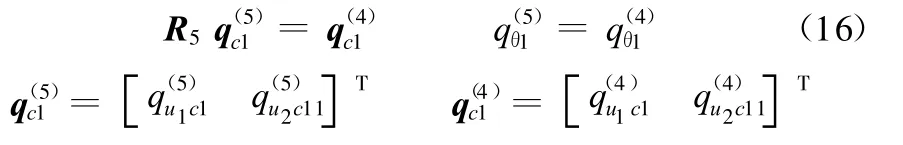
子結構(6)可視為固支梁,與子結構(3)在C點的變形協調條件可表示為

子結構(7)可視為鉸支固支梁,子結構(9)可視為鉸支梁,則二者與子結構(6)在F點的變形協調條件為

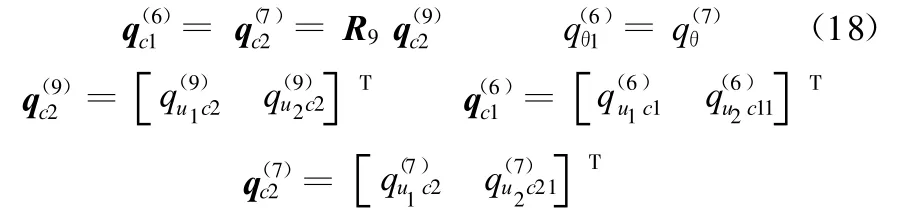
子結構(8)可視為鉸支梁,其與子結構(7)在G點的變形協調條件可表示為

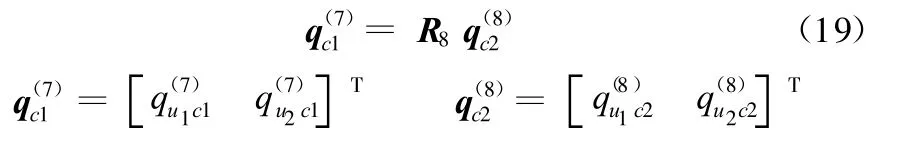
子結構(8)與(9)在H點的變形協調條件可表示為

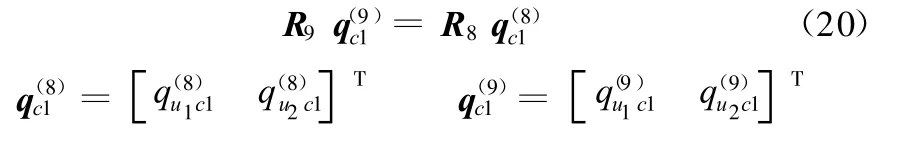
兩個電機作為集中質量作用在F點和C點,用qm1和qm2表示電機1和2的模態坐標,并且有變形協調條件:

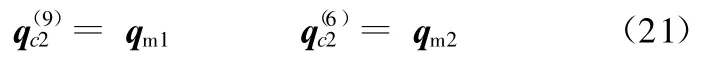
把以上變形協調條件寫成矩陣形式:

取B中27個線性無關的列向量構成矩陣Ba,其余列向量記為矩陣BI,其相應的廣義坐標分別為qa和qI,則

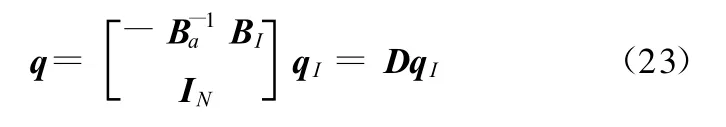
式中 N=19。擴展到所有模態坐標,進一步可導出:

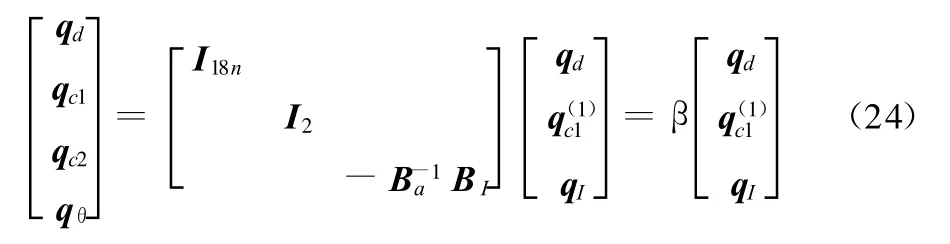
把子結構動力學控制方程組集合起來,可得到質量陣M和剛度陣K,引入變形協調條件后系統的彈性動力學模型為

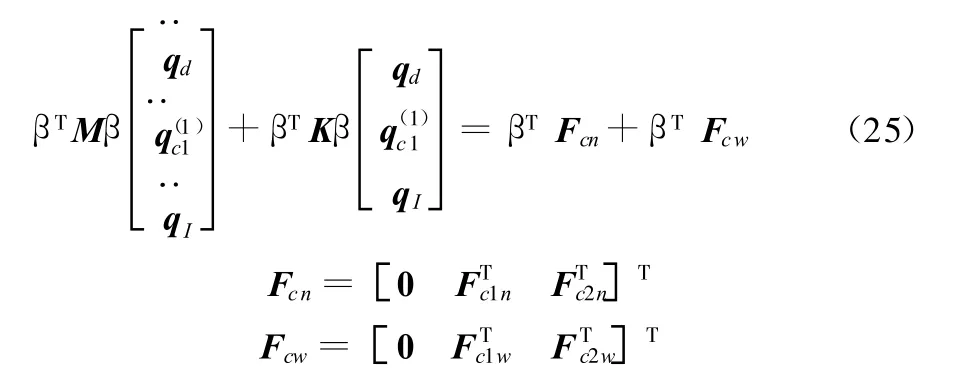
因為對接力為內力,大小相等,方向相反,可證明 βTFcn=0。

3 動力學仿真

利用上述模型考察車載機械手的低階固有頻率隨幾何參數的變化規律,以及低階模態對機械手末端振動的貢獻,系統中的物理參數如表1所示。圖4所示為系統一、二、三階固有頻率隨搖桿、伸縮桿套、伸縮桿和手爪控制桿截面尺寸(矩形空心截面、壁厚不變)的變化規律。

表1 物理參數

圖4a示出了搖桿截面尺寸對系統固有頻率f的影響規律。由圖4a可見,當矩形截面邊長slOB在50mm和150mm之間變化時,一階固有頻率隨著截面邊長的增大而增大,頻率變化范圍為4.4～8.4Hz;當截面邊長大于150mm時,一階固有頻率變化甚微,但二階固有頻率隨著截面邊長的增大而快速增大,變化范圍為10～30Hz;而搖桿截面尺寸對三階固有頻率影響很小。

圖4b示出了伸縮桿套截面尺寸對系統固有頻率的影響規律。由圖4b可見,伸縮桿套截面邊長slCE對一、二階固有頻率影響很小;當截面尺寸為50～70mm,三階固有頻率隨著截面尺寸的增大而增大,頻率的變化范圍為52～54Hz,當截面尺寸大于70mm時,三階固有頻率下降很快。

圖4c示出了伸縮桿截面尺寸對系統固有頻率的影響規律。由圖4c可見,當矩形截面邊長slG C在50mm和100mm之間變化時,一階固有頻率隨著截面邊長的增大而增大,頻率變化范圍為6.1～9.1Hz;當截面邊長大于120mm時,一階固有頻率變化甚微,但二、三階固有頻率隨著截面邊長的增大而快速增大,二階固有頻率的變化范圍為11～26Hz,而三階固有頻率的變化范圍為41～130Hz。

圖4d示出了手爪控制桿截面邊長slGHE對系統固有頻率的影響規律。由圖4d可見,手爪控制桿截面尺寸對低階固有頻率的影響甚微。

基于以上分析,對低階固有頻率影響較大的為搖桿和伸縮桿的截面尺寸。二者截面尺寸對低階固有頻率的影響,以及搖桿和伸縮桿截面尺寸對低階固有頻率的影響規律如圖5所示。由圖5可見,增大搖桿和伸縮桿的截面尺寸可顯著提高車載機械手的低階固有頻率。

4 結論

①提出將車載機械手分解成若干子結構,在建立各自動力學模型后,借助邊界條件經綜合得到系統的動力學方程的建模策略和分析方法。該方法易于實現、計算效率高,便于討論結構參數對系統低階模態的影響規律。②增大搖桿和伸縮桿截面尺寸可明顯提高機械手的低頻特性。③在液壓作動器的作用點設置邊界坐標,可方便基于動力學特性的控制模型的導出,為機械手的振動控制提供了理論基礎。

[1]Agrawal O P,Shabana A A.Dynamic Analysis of Multi—bodySystems UsingComponent Modes[J].J.Computer and Structure,1985,21(6):67-70.

[2]Sunada W,Dubowsky S.The Application of Finite Element M ethodsto theDynamicAnalysisof Flexible Spatial and Co—Planar Linkage Systems[J].J.Mech.Design,1981,103(3):643-651.

[3]崔玲麗,張建宇,高立新,等.柔性機械臂系統動力學建模的研究[J].系統仿真學報,2007,19(6):1205-1208.

[4]王樹新,蔣鐵英,張鐵民,等.柔性機械臂的動力學分析與實驗研究[J].中國機械工程,1995,6(6):18-20.

[5]Johanni R.On the Automatic Generation of the Equations of Motion forRobots with Elastically Deformable Arms[C]//Proc.of IFAC Symp.on Theory of Robots.Vienna,Austria,1986:195-199.

[6]李光,吳敏.液壓柔性機械臂的動力學建模及魯棒控制研究[J].液壓與氣動,2005(4):1-4.

[7]曹學民,黃之初.柔性機械手動力學研究[J].武漢理工大學學報,2006,28(8):81-84.

[8]Bellezza F,Lanari L,Ulivi G.Exact Modeling of the Flexible SlewingLink[C]//Proc.of IEEE Int.Conf.Robotics and Automation.Cincinnati,OH,USA:IEEE,1990:734-739.

[9]徐晨,傅瑜.FRM建模方法與精度的研究[J].電子科技雜志,1999(3):1-12.

[10]郭木河,張戎軍,孫增新,等.柔性機械手的建模與控制[J].控制與決策,1998,13(1):3-6.

[11]張汝青,殷學綱,董明.計算結構動力學[M].重慶:重慶大學出版社,1987.

[12]王文亮,杜作潤.結構振動與動態子結構方法[M].上海:復旦大學出版社,1985.