秩1修正矩陣特征值問題的推廣及其應用

呂海玲，明清河

(1．棗莊學院 信息科學與工程學院，山東 棗莊 277160;2．棗莊學院 數學與統計學院，山東 棗莊 277160)

1 Introduction

In this paper we prove a spectral perturbation theorem for an extension eigenvalues of rank－ one update matrix of special structure，which shows how to modify r eigenvalues of a matrix of order n，(r≤n)，ia a rank－k updated matrix，without changing any of the n－rremaining eigenvalues．This theorem plays a relevan t role in the study of the nonnegative inverse eigenvalue problem(NIEP)．The main idea behind our proof is from the simple relation between the determinants of a matrix and this result，using a well known determinant identity．Furthermore，we extent this theorem to the block eigenvalues problem．By using this extension，we give a Application on eigenvalues problem of matrix perturbation of special structure．

Because we apply a classic determinant equality to our spectral analysis，we are able to find explicit expression of the characteristic polynomial of the rank－r update matrix．All eigenvalues of the matrix are immediately available．

Lemma1 If A is an invertible n×n matrix，and u and v are two n－dimensional column vectors，then

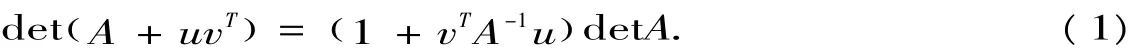
Proof．We may assume A=I，the n × n identity matrix，since then(1)follows from

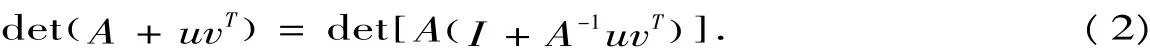
in the general case．In this special case，the result comes from the equality

so(2)becomes

Remark1 If A is an invertible n×n matrix，B is a n×r matrix，C is a r×n matrix，then

In the next section we present the main result．

2 Main result

Let A be an n×n matrix．The eigenvalues of A are all the complex zeros of the characteristic polynomial pA(λ)=det(λI－ A)of A．Letσ(A)= {λ1，λ2，…，λn}be the set of the eigenvalues of A，counting algebraic multiplicity，that is spectrum of A．

Theorem 1［1］Let u and v are two n － dimensional column vectors such that u is an eigenvector of A associated with eigenvalue λ1． Then，the eigenvalues of A + uvTare {λ1+vTu，λ2，…，λn}，counting algebraic multiplicity．

The following result is an extension of the theorem 1．This extension shows how to change r eigenvalues λ1，λ2，…，λr，r≤ n，of a matrix A of order n，via a rank － k updated matrix，without changing any of the n － rremaining eigenvaluesλr+1，λr+2，…，λn．

繼上海之后，云南第二個獲得設立人民幣國際投貸基金的試點資格，人民幣國際投貸基金落戶云南，且啟動了首單人民幣國際投貸基金海外投資項目，為推動人民幣“走出去”探索了新路徑，為企業“走出去”搭建了新平臺。

Theorem 2 Let A be an n × n matrix with eigenvalues λ1，λ2，…，λn．Let X =[x1x2…xr]be such that rank(X)=r and AX=Xdiag [λ1，λ2，…，λr]，r≤n．Let C be a r × n matrix．Then the matrix A+XC has eigenvalues γ1，γ2，…，γr，λr+1，λr+2，…，λn．where γ1，γ2，…，γrare eigenvalues of the matrix K+CX with K=diag [λ1，λ2，…，λr]．

Proof Letλ ? σ(A)be any complex number．Then，by applying remark 1 to the equality

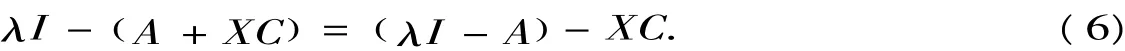
W e have

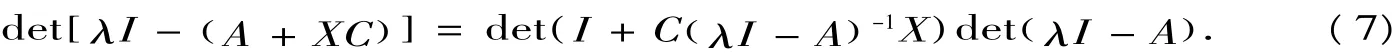
The condition AX=Xdiag [λ1，λ2，…，λr]implies that

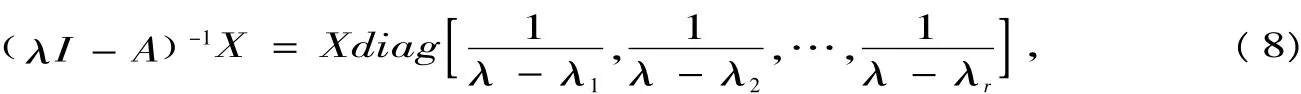
so(7)becomes

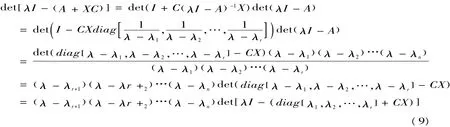
Since the above equality is true for allλ ? σ(A)，the theorem is p roved．

Remark2．2 Since A and AThave the same eigenvalues counting algebraic multiplicity，the conclusion of Theorem 2．1 also holds for A+XC，where X= [x1x2… xr]be such that rank(X)=r and AX=Xdiag [λ1，λ2，…，λr]．

Furthermore，we extent this theorem to the block eigenvalues problem

Definition 1［4］．A matrix X of order n is a block eigenvalue of a matrix A of order mn，if there exists a block vector V of full rank，such that AV=VX，X is a block eigenvector of A．

The matrix A is partitioned into m ×m blocks of order n，and the block vector V．

Definition 2［4］．A set of block eigenvalues of a block matrix is a complete set if the set of all the eigenvalues of these block eigenvalues is the set of the matrix．

Let us suppose now that we have computed mn scalar eigenvalues of a partitioned matrix A．We can construct a complete set of block eigenvalues by taking m matrix of order n in Jordan form where the diagonal elements are those scalar eigenvalues．Furthermore，if the scalar eigenvalues of A are distinct，these m matrix are diagonal matrix as is shown in the following construction:

where theλi，i=1，…，mn，are the eigenvaluesof A．The proof that the matrix Xj，j=1，…，m，are a complete set of block eigenvalues of A is in［1，p．74］．

Theorem 2．If the scalar eigenvalues of A are distinct，let V and C be the block vectors such that V is a block eigenvector of A associated with block eigenvalues X1，Then，the eigenvalues of A + VCTare μ1，…，μn，λn+1，…，λ2n，…λ(m－1)n+1，…，λmnwhere μ1，…，μnare eigenvalues of the matrix K+CTV with K=diag［λ1，…，λn］．Proof．The same to theorem 1．

3 Application of the theorem

A direct consequence of Theorem 2．1 is the following．

One Application of the result is given to illustrate the eigenvalues problem with the perturbation matrix．

Proposition 3．1Let A，B，C，D ∈ Cn×n，D=A+B，where B is the perturbation of A．If B=XC，where X= ［x1，x2，…，xn］，xiis an eigenvector of A dissociate with eigenvalue xi，i=1，2，…，n．So thatthen，the eigenvalues of A+B are the eigenvalues of the matrix diag［λ1，λ2，…，λn］+CX．

［1］Jiu D，Zhou A H．Eigenvalues of rank －one updated matrix with some applications［J］．Applied Mathematics Letters，2007，20:1223－1226．

［2］Ricrdo L S，Oscar R．Applications of a Brauer theorem in the nonnegative inverse eigenvalue problem［J］．Linear Algebra and its Applications，2006，416:844 －856．

［3］Bapat R B，Raghavan E S．Nonnegative Matrices and Applications，Cambridge University press，1997．

［4］Dennis J E，Traub J F and Weber R．P．On the matrix polynomial，lambda－ matrix and block eigenvalue problem，Tech．Rep．71 － 109，Computer Science Department，Cornell Univ，Ithaca，NY and Carnegie － Mellon Univ．，Pitsburgh，PA，(1971)．