高血壓腦出血術后并發肺部感染的中醫護理方法和效果
羅梅艷
高血壓腦出血是腦血管疾病中致死率及致殘率非常高的一種疾病,且發病迅速,在此種狀態下,患者會出現不同程度的嘔吐、頭部疼痛以及昏迷癥狀,會對患者的生命安全產生嚴重的威脅[1]。通過研究發現,導致腦出血最主要的因素主要來源于高血壓,當患者的血壓驟然升高之后,血管薄弱處將會極其容易出現破裂,從而導致患者腦出血;而肺部感染是高血壓腦出血患者中一種最為常見的并發癥,所以,對于患者采取有效的治療以及護理非常的重要[2]。本研究對于本院的80例高血壓腦出血手術后并發肺部感染患者采用不同的護理方式,對于兩組患者的臨床療效以及護理滿意度進行比較,現進行報告如下。
1 資料與方法
1.1 一般資料 選取我院2018年5月—2019年5月的高血壓腦出血手術后并發肺部感染患者80例。本研究經過院醫學倫理委員會審核批準,患者對本次研究知情。其中,觀察組男21例,女19例;年齡最小為55歲,最大為74歲,平均年齡為(66.2±2.8)歲。對照組男23例,女17例;年齡最小為57歲,最大為77歲,平均年齡為(69.8±2.9)歲。對2組患者的資料比較,差異不具備統計學意義(P>0.05)。
1.2 診斷標準 所有患者均需要滿足《2015 中國腦出血診療指導規范》中的相關診斷標準,并且術后均呈出現肺部感染的癥狀。
1.3 納入標準 所有患者均意識清晰,臨床資料完整,對于本次研究積極配合,并且簽署知情同意書。
1.4 方法
1.4.1 治療方法 對照組患者采用常規護理,密切觀察所有合并癥患者的體征表現,主要體現為對患者進行呼吸性質觀察、施以顱內壓監測,并監測患者的血氧飽和度、密切的觀察患者的排泄情況等,保障患者的呼吸道通暢。高血壓腦出血患者通常會在表現出生理反射減退的情況以及意識不清醒的情況,之后會出現呼吸道分泌物阻塞的現象,如果不及時處理的話,將會導致患者肺部感染。患者一旦發生呼吸道分泌物排出障礙的問題,護理人員需要對患者實施氣管切開操作,并且需要對患者采取呼吸機進行輔助護理干預。除此之外,護理人員還需要對患者進行護理干預,在患者實施手術治療期間,需要加強對患者口腔護理的力度,避免發生口腔感染。在進行口腔護理的時候,需要檢測患者的口腔分泌物并培養,選擇合理的漱口液干預。在對患者實施治護的過程中,對于需要進行無菌操作的,需要嚴格遵守相關規則,避免醫源性因素導致患者的病情嚴重。觀察組患者采用中醫護理辨證施護:高血壓腦出血術后并發肺部感染患者需要以患者的病情表現實施針對性的施護。在護理期間,需要密切的觀察患者的臨床表現以及生命體征表現,并以此為基礎來選擇合理的中藥輔助治療。如果是存在痰濕阻滯癥狀,就需要選擇溫性食物對患者進行食療干預;患者如果存在風熱多痰癥狀,那么就需要選擇星萎承氣湯加以輔助治療干預;患者如果出現脈絡不通及血流不暢的情況,需要對患者開展針對性的飲食護理干預;患者如果出現血流不暢的癥狀,則要采用通絡益氣類中藥加以治療干預[3]。采用循經拍背護理:循經拍背是一種常見的中醫護理方式,其分為拍法和擊法。具體方法為沿患者脊柱和脊柱兩側足太陽膀胱經由上至下進行叩擊或拍打,拍打過程中保持力度適中,盡量加大力度到患者最大耐受限度,拍背的過程中應保持動作緩慢溫柔,避免患者因拍打過快或用力過猛而產生嗆咳的情況。每日為患者拍背2~3次,每次拍背時間控制在30 min左右[4]。在患者入院后病情保持穩定時,護理人員可給予其指壓天突穴護理,首先讓患者保持坐位,用一手將患者背部扶住一手于患者胸骨上窩的天突穴處,并將中指和食指緊貼于患者的喉部,不斷按壓以促使患者咳嗽,從而起到促排痰的作用。每次按壓時間控制在1~5 min,按壓過程中患者未出現刺激性咳嗽時應再次進行按壓,直至患者產生刺激性咳嗽時停止,每日為患者按壓2次。對于疼痛患者實施穴位按摩,穴位選擇百會、風池、太陽等。
1.4.2 觀察指標與療效判定標準 對于2組患者的護理總有效率比較。顯效:在經過護理之后,患者的呼吸恢復平順,自身的血氧飽和度水平呈現顯著升高,肺部痰鳴音癥狀得到明顯的減輕,咳出的痰液稀薄,并且顏色轉變為白色,對于患者的胸部 X 線片檢查結果以及血常規檢查結果進行觀察,并未發生感染征兆,或者感染癥狀有所緩解;有效:觀察患者的胸部 X 線片檢查以及血常規檢查,感染癥狀有所緩解,但是咳出的痰液仍然黏稠,患者的血氧飽和度水平出現一定程度上的上升,肺部痰鳴音得到明顯的減輕;無效:在實施護理之后,患者的上述表現均未獲得改善,甚至出現加重情況。護理滿意度分為非常滿意、滿意以及不滿意。
1.4.3 統計學方法 采用統計學軟件SPSS 17.0分析和處理數據,采用%來表示計數資料,且施以χ2檢驗。P<0.05表示數據對比具有統計學意義。
2 結果
2.1 2組患者的護理總有效率比較 經過對于2組患者實施不同的護理措施,觀察組患者的護理總有效率高于對照組,差異具有統計學意義(P<0.05)。見表1。
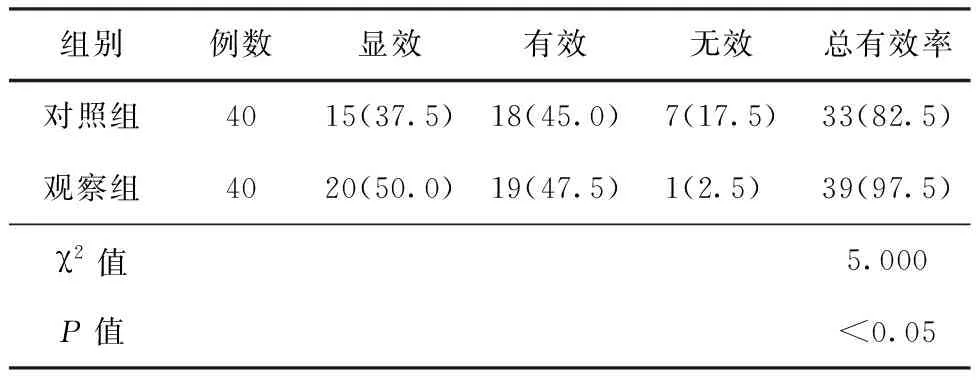
表1 2組患者的護理總有效率對比 (例,%)
2.2 2組患者的護理滿意度比較 經過護理之后,觀察組患者的滿意度為97.5%,對照組護理后的滿意度為67.5%,觀察組患者高于對照組,差異同樣具有統計學意義(P<0.05)。見表2。
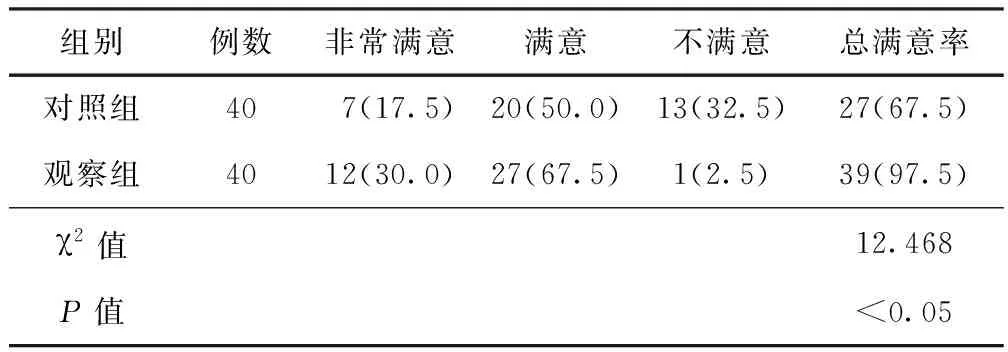
表2 2組患者的護理滿意度比較 (例,%)
2.3 2組患者的住院時間比較 經過護理之后,比較2組患者的住院時間,觀察組比對照組的時間短,差異存在著統計學意義(P<0.05)。見表 3。
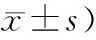
表3 2組患者的住院時間比較 (例,
3 討論
高血壓腦出血是當前一種具有較高病死率的疾病,患病之后將會對患者的身體健康以及生命安全造成嚴重的影響,近年來雖然對于該病的研究一直在進行,但是在目前仍舊具有較高的病死率,并且存活的患者大部分都存在著不同程度上的殘疾[5]。因此,提高患者的臨床治療效果可以有效地改善患者的生活質量,所以對患者采用有效地臨床護理具有十分重要的作用。而在高血壓腦出血患者中最為常見的術并發癥之一就是肺部感染,如果患者沒有得到及時有效地治療,將會出現呼吸功能障礙,甚至出現呼吸衰竭,此時將會具有潛在的死亡威脅[6]。高血壓腦出血患者出現肺部感染有很多的因素,但主要表現在:①患者術后的身體比較虛弱,并且機體在此時的免疫能力非常低,導致患者極易感染;②對患者的留置胃管反復吸痰的話將會對呼吸道造成創傷,在呼吸過程中患者如果誤入下呼吸道將會出現肺部感染;③在手術前后患者所處的環境也在一定程度上會誘發肺部感染。而在治療患者的過程中,如果醫護人員使用的醫用器具消毒不徹底、空氣流通不暢等問題均會導致肺部感染;④由于大部分的高血壓腦出血患者都是老年人,所以,機體免疫能力相對較差,并且肺部組織也會出現不同程度的萎縮,這一因素也是導致患者肺部感染的主要因素。而中醫護理具有成本小的優勢,并且在經過治療后產生的不良反應也比較的小,效果持續時間長[7]。
中醫辨證可以說是中醫學的精髓,對于高血壓腦出血術后并發肺部感染患者采用中醫辨證進行護理干預,可以將扶正祛邪的護理效果充分發揮出來,并且還可以根據患者的實際疾病證型采取針對性的施護,可以充分發揮出通補兼施、補虛瀉實以及寓通于補的效果,獲得標本兼治的良好效果。對患者實施循經叩背法進行干預,可以明顯改善患者的術后咳痰困難癥狀,并且配合指壓天突穴干預后,可以有效地抑制肺部感染。本次研究中,對于高血壓腦出血手術后并發肺部感染患者選擇中醫護理方法具有顯著的護理效果[8]。
本研究通過對于本源的80例高血壓腦出血手術后并發肺部感染患者采取不同的護理方法,結果顯示,觀察組患者的護理滿意度為97.5%,對照組患者的護理滿意度為67.5%,觀察組比對照組的護理滿意度高,差異有統計學意義(P<0.05);對于2組患者的治療有效率比較,觀察組患者要比對照組患者的治療效果好,差異存在著統計學意義(P<0.05);而對于2組患者的住院時間進行比較,結果顯示,觀察組患者要比對照組患者的時間短,差異存在統計學意義(P<0.05)。
綜上所述,在高血壓腦出血術后并發肺部感染的患者中采用中醫護理方法,可以提高患者的臨床治療效果具有良好的作用,并且還可以降低并發癥的發生率,建議在臨床中推廣應用。

