pk元域上的二次方程與三次方程

孫宗明

(泰山學院數學與系統科學學院，山東泰安 271021)

設F是一個pk元域，關于F上的二次方程與三次方程，對已有的研究成果進行綜述，并給出這一課題研究步步深入的過程，同時，綜述F的單超越擴域E上的二次方程的結果以及F上的三項方程的一些結果.本文中，0表示域的零元，e表示域的單位元.

1 F上的二次方程

筆者于1981年發表的第一篇數學文章［1］(也是首次公開發表的文章)，研究了素數模p(p≥3)的二次同余方程，得到下面的

定理1.1 設有ax2+bx+c≡0(modp)，a關于模p不為0，且素數p≥3，記△≡b2－4ac，m=(p－1)/2，則其根的狀況為:

當p=2時，［1］沒有徹底解決問題，實際上，有下面的

定理1.2 設有ax2+bx+c≡0(modp)，a關于模p不為0，且素數p=2，當b關于模p不為0時取d，使bd≡1(modp)，記△=acd2，則其根的狀況為:

實際上，素數p為模的二次同余方程就是p元域Fp上的二次方程，于是，就有下面的

定理1.3 設有p元域Fp上的二次方程ax2+bx+c=0(a≠0)，p≥3，△=b2－4ac，m=(p－1)/2，則其在Fp中的根的狀況是:

1)在Fp中有兩個不同的根△m=e;

2)在Fp中有兩個相同的根△m=0;

3)在Fp中沒有根△m=－e.

定理1.4 設有p元域或Fp上的二次方程ax2+bx+c=0(a≠0)，p=2，則其在Fp中的根的狀況是:

1)在Fp中有兩個不同的根b≠0且acb－2=0;

2)在Fp中有兩個相同的根b=0;

3)在Fp中沒有根b≠0且acb－2=e.

筆者在1980年寫成的［2］于1983年發表，得到下面的

定理1.5 設有F上的二次方程ax2+bx+c=0(a≠0)，p≥3，△=b2－4ac，m=(pk－1)/2，則其在F中的根的狀況是:

［2］沒有徹底解決p=2的情況，［2］發表后，上海交通大學沈灝先生來信給筆者，討論［2］中所遺留的p=2的有關問題，至1984年，沈灝先生來信告訴筆者，他的學生完整地解決了p=2的情況，就是于1986年發表的［3］，給出了下面的

定理1.6 設有F上的二次方程ax2+bx+c=0(a≠0)，p=2，當b≠0時，設β=acb－2，Tk(β)=，則其在F中的根的狀況是:

2 F上的三次方程

武漢大學宋雪清以筆者的［2］為參考文獻寫成［4］，研究p＞3時F上的三次方程，于1986年發表;對于［4］中的遺留問題，湛江師范學院李慶寫成［5］，于1990年發表，從而徹底地解決了p＞3的情況;筆者以［4］與［5］為參考文獻寫成［6］，于1993年發表，解決了p=2的情況;按照［6］的模式，筆者將［4］與［5］進行整理加工而寫成［7］.

先研究p＞3的情況，有如下的定理2.1與定理2.2以及為證明定理作準備的6條結論，下面按［7］列出.

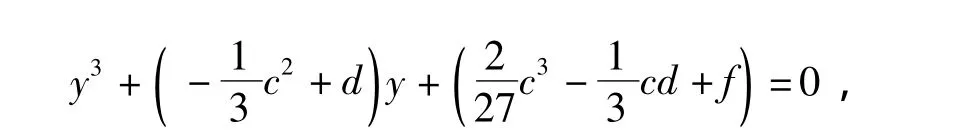
二者的根的狀況相同，并且，相應的根x0與y0有關系于是，研究F上的三次方程可以僅研究F上的方程x3+ax+b=0(a≠0，b≠0).

2)若y0，z0∈F是方程=0在F中的二個根，則可以使，并且，x0= y0+z0是方程x3+ax+b=0(a≠0，b≠0)在F中的根.

3)在F中，若

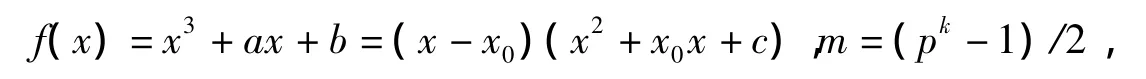
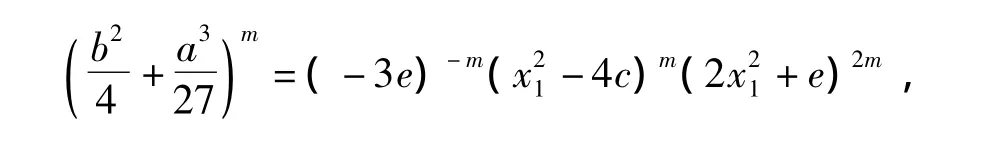
則有其中x0是方程x3+ax+b=0(a≠0，b≠0)在F中的一個根.

4)設m=(pk－1)/2，k為偶數，則(－3e)m=e.

5)設m=(pk－1)/2，k為奇數，則有:①當3|(pk－1)時，(－3e)m=e;②當3不整除pk－1時，(－3e)m=－e.

6)設d∈F，3|(pk－1)，n=(pk－1)/3，則dn只能是0，e，α，α2之一，其中α是F*中的一個3階元素.

定理2.1 設3不整除pk－1，m=(pk－1)/2，△=，則F上的方程x3+ax+b=0(a≠0，b≠ 0)在F中的根的狀況是:

1)△m=e當k為偶數時，其在F中有三個互異的根;當k為奇數時，其在F中有且僅有一個根;

2)△m=0其在F有一個單根與一個二重根;

3)△m=－e或其在F中沒有根;或當k為偶數時，其在F中有且僅有一個根;或當k為奇數時，其在F中有三個互異的根.

定理2.2 設3|(pk－1)，m=(pk－1)/2，△，則F上的方程x3+ax+b=0(a≠0，b≠0)在 F中的根的狀況是:

1)△m=e當==e時，其在F中的三個互異的根;當=α，=α2或=α2，=α時，其在F中沒有根，其中△1，△2是方程=0在F中的兩個不同的根，n=(pk－1)/3，α是F*中的一個3階元素;

2)△m=0其在F有一個單根與一個二重根;

3)△m=－e當=e時，其在F中有且僅有一個根;當或，時，其在F中沒有根，其中△1，△2是方程=0在F(ω)中的二個不同的根，ω2=△，n'=(p2k－1)/3，α是F*中的一個3階元素.

再研究p=2的情況，有如下的定理2.3與定理2.4以及為證明定理作準備的6條結論，下面按［6］列出.

1)設x=y+c，則F上的方程x3+cx2+dx+f=0變為

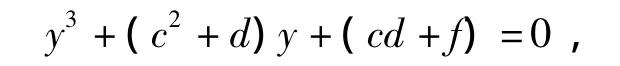
二者的根的狀況相同，并且，相應的根x0與y0有關系x0=y0+c.于是，研究F上的三次方程可以僅研究F上的方程x3+ax+b=0(a≠0).

2)若y0，z0∈F是X2+bX+a3=0在F中的兩個根，則可以使x0y0=a，并且，x0=y0+z0是方程x3+ax+b=0(a≠0)在F中的根.

3)設△∈F，則有:①當3不整除2k－1時，y3=△在F中有唯一的根;②當3|(2k－1)時，y3=△在F中有根△n=e，并且，當有根時，若記一個根為y0，則三個互異的根是y0，αy0，α2y0，其中n=(2k－1)/3，α是F*中的一個3階元素.

5)設3|(2k－1)，n=(2k－1)/3，若△1，△2是X2+bX+a3=0在F中的兩個互異的根，則有且僅有下列三種情況:①==e;②=α，=α2;③=α2，=α，其中α是F*中的一個3階元素.

6)若f(x)為F上的n次不可約多項式，δ為f(x)的一個根，則F關于f(x)的分裂域F(δ)對于F的次數為n，即(F(δ):F)=n，從而|f(δ)|=2nk.

定理2.3 設3不整除2k－1，則F上的方程x3+ax+b=0(a≠0)在F中的根的狀況是:

1)當b=0時，其在F中有三個根x1=0，x2=x3=.

i)其在F中無根;

ii)其在F中有根，取其一個根記為x0，

定理2.4 設3|(2k－1)，n=(2k－1)/3，α是F*中的一個3階元素，則F上的方程x3+ax+b=0 (a0)在F中的根的狀況是:

1)當b=0時，其在F中有三個根x1=0，x2=x3=

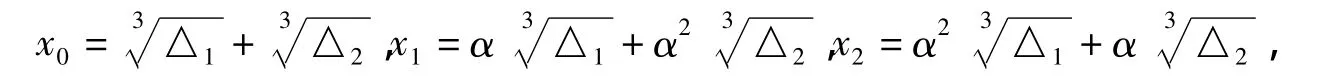
對于p=3的情況，筆者與另外兩位代數學同行寫成［8］，于1995年發表，并且，筆者后來又寫成［9］，于2001年發表，但是，尚未得到較滿意的解決，有如下的定理2.5與定理2.6.

設F上的方程x3+ax2+bx+c=0()在F中有一個根d，而x=y+d，則可以轉化為對方程y2+ay +(2ad+b)=0( )的討論.

定理2.5 當方程( )在F中有根y0時，方程()在F中有根x0=y0+d.對于方程()在F中的又一個根f，且fd，則f－d是方程( )在F中的一個根.

定理2.6 設m=(pk－1)/2，則F上的方程x3+ax2+bx+c=0()在F中的根的狀況是:

1)其在F中沒有根.

2)其在F中有根，取其一根d，記△=a2－(2ad+b)，

i)當△m=0時，其在F中有一根d與二重根y0+d，其中y0為方程()在F中的二重根;

ii)當△m=e時，其在F中有三個互異的根d，y1+d，y2+d或有一根y2+d與二重根d，其中y1，y2為方程()在F中的二個互異的根;

iii)當△m=－e時，其在F中有一個根d.

3 E上的二次方程

設E是F的單超越擴域，由［10］知，F上的未定元的有理函數域F(x)與E同構，從而就記E= F(x).本款中，F的元素用a，b，c，…表示，E的元素用A，B，C，…表示;為方便，將單位元e記為1.對于E上的二次方程Ay2+By+C=0(A≠0)，筆者寫成［11］，于1992年發表.對此，列出下面的6條結論及定理3.1與定理3.2.

1)設A∈E，n為正整數，若存在B∈E，使得Bn=A，則稱A是E的一個n方元素.

2)E中的任一個非零元素A均可以寫為A=f(x)/g(x)，其中f(x)，g(x)∈F［x］，且(f(x)，g(x)) =1，f(x)或g(x)的首相系數為1.

5)設n為正整數，A≠0，A∈E，則E上的方程yn=A在E中有根存在f1(x)，g1(x)∈F［x］，(f1(x)，g1(x))=1，f1(x)的首項系數為1，使得

6)設E的特征數p=2，而z2+z=f(x)/g(x)是E上的方程，其中f(x)，g(x)∈F［x］，(f(x)，g(x)) =1，g(x)的首項系數為1，則其在E上有兩個不同的根存在f1(x)，g1(x)∈F［x］，(f1(x)，g1(x))= 1，g1(x)的首項系數為1，并且

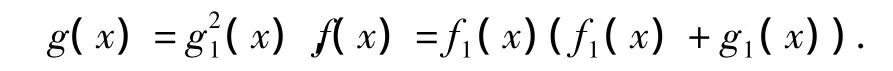
定理3.1 設域E的特征數p≥3，Ay2+By+C=0(A≠0)是E上的二次方程，△=B2－4AC，則其在E中的根的狀況是:

定理3.2 設域E的特征數p=2，Ay2+By+C=0(A≠0)是E上的二次方程，則其在E中的根的狀況是:

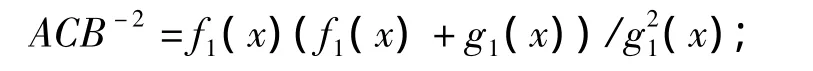
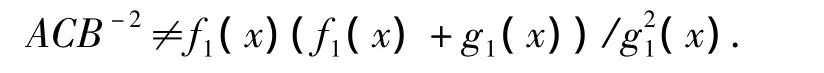
4 二次方程的根的公式

對于2k元域F上的二次方程，筆者曾就一種情況得到根的表示公式，寫成［12］，于2001年發表;后來，鄭州解放軍信息學院王念平進行了研究，寫成［13］，于2004年發表;筆者認為，這一問題尚待進一步研究，此處從略.

5 二項方程

在［2］與［6］等文章中，已經討論了方程y2=△與y3=△等，就一般情況而言，引導至F與E上的二項方程，筆者寫成［14］，于2001年發表.

定理5.1 設s=(n，pk－1)，u=(pk－1)/s，xn=d(d≠0)是F上的二項方程，則其在F中的根的狀況是:

2)其在F中有(n，pk－1)個單根du=e且p不整除n;

3)其在F中有(n，pk－1)組互異的pl重根du=e且pl|n但pl+1不整除n.

定理5.2 設s=(n，pk－1)，xn=D(D≠0)是E上的二項方程，則其在E中的根的狀況是:

2)其在E中有(n，pk－1)個單根D是E的n方元素且p不整除n;

3)其在E中有(n，pk－1)組互異的pl重根D是E的n方元素且pl|n但pl+1不整除n.

6 三項方程

筆者的文章［2］發表后，上海交通大學沈灝先生來信給筆者，討論［2］中所遺留的p=2的有關問題，至1984年，沈灝先生來信告訴筆者，他的學生完整地解決了p=2的情況，筆者根據信中的結果和文章［2］寫成文章［15］，于1987年發表，給出了下面的定理6.1與定理6.2.

定理6.1 設有F上的一類2ps次方程

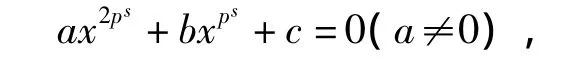
其中p≥3，s為非負整數，記

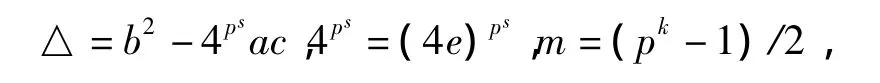
則其在F中的根的狀況是:

1)其在F中有兩組不同的ps重根△m=e;

2)其在F中有2ps重根△m=0;

定理6.2 設有F上的一類2ps次方程

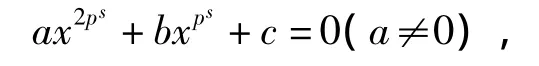
Ω=acb－2，其中p=2，s為非負整數，則其在F中的根的狀況是:

1)其在F中有兩組不同的ps重根Tk(Ω)=0;

2)在F中有2ps重根b=0;

上面的方程就是一個三項方程，是由二次方程引發的一種方程，在研究的過程中要用到二次方程的結果.筆者繼續研究F上的三項方程:對于異于p的素數q，研究了ax2q+bxq+c=0，寫成［16］，于1990年發表;對于一般的正整數n，研究了ax2n+bxn+c=0，寫成［17］，于1991年發表;但是，所得的結果較上面的定理6.1與定理6.2復雜得多，此處從略.

借助于F上的三項方程的結果，利用E上的二次方程和二項方程的結果，筆者研究了E上的三項方程Ay2n+Byn+C=0，寫成［18］，于2000年發表，此處亦從略.

7 一類方程

筆者寫成的［19］，借助于F上的二項方程的結果，研究了F上的一類方程，于1996年發表.后來，筆者又相繼發表了［20－23］.

定理7.1 F上的方程

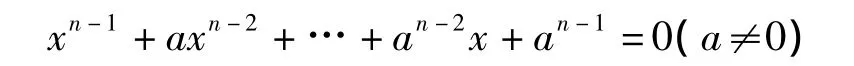
在F中的根的狀況是:

2)其在F中有(n，pk－1)－1個單根(n，pk－1)≠1且p不整除n;

3)其在F中有(n，pk－1)組互異的重根，其中一組為pl－1重根a，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

定理7.2 當n為偶數時，F上的方程

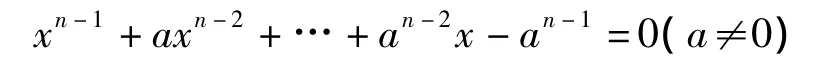
在F中的根的狀況是:

2)其在F中有(n，pk－1)－1個單根(n，pk－1)≠1且p不整除n;

3)其在F中有(n，pk－1)組互異的重根，其中一組為pl－1重根－a，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

定理7.3 當n為奇數時，F上的方程

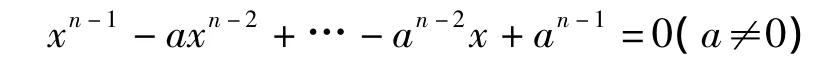
在F中的根的狀況是:

2)其在F中有(n，pk－1)－1個單根(n，pk－1)≠1且p不整除n;

3)其在F中有(n，pk－1)組互異的重根，其中一組為pl－1重根－a，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

筆者借助于［23］寫成［24］，研究了E上的一類方程，于2007年發表.

定理7.4 E上的方程

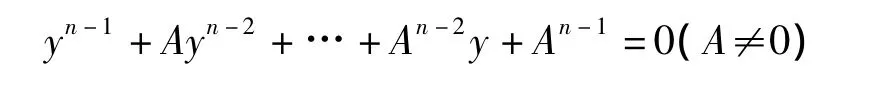
在E中的根的狀況是:

2)其在E中有(n，pk－1)－1個互異的單根(n，pk－1)≠1且p不整除n;

3)其在E中有(n，pk－1)組互異的重根，其中一組為pl－1重根A，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

定理7.5 當n為偶數時，E上的方程

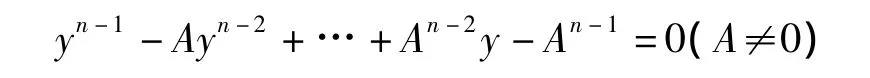
在E中的根的狀況是:

2)其在E中有(n，pk－1)－1個單根(n，pk－1)≠1且p不整除n;

3)其在E中有(n，pk－1)組互異的重根，其中一組為pl－1重根－A，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

定理7.6 當n為奇數時，E上的方程

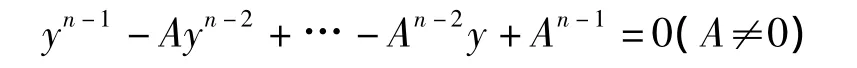
在E中的根的狀況是:

2)其在E中有(n，pk－1)－1個單根(n，pk－1)≠1且p不整除n;

3)其在E中有(n，pk－1)組互異的重根，其中一組為pl－1重根－A，而其余組(若還有的話)均為pl重根(n，pk－1)≠1，且pl|n但pl+1不整除n.

8 某些方程

［25］與［26］研究了p2k元域Fq2(q=pk)上的方程xq+1=λ和x+xq=μ在Fq2中的根的狀況以及Fq2上的方程在Fq2中的解的個數.

［27］研究了p元域Fp上的方程xp－x－a=0在Fp上的根的狀況，后來，筆者又研究了pk元域F上的方程xps－x－a=0在F中的根的狀況，寫成［28］.

［29］研究了群中的方程xn=e的解的個數，此后，在上面所列的文獻中，作為F上的方程研究了其在F中的根的狀況，并多次用到該結論，［30］再次詳細地研究了其在F中的根的狀況.

［31］將［32］中關于數域上線性矩陣方程(組)的理論推到pk元域F上.

［33－40］就有限域上方程根的求法、不可約多項式、因式分解、n方元素等問題進行了一定的研究.

9 結束語

該文是一篇綜述性的文章，此前，［41－44］也曾對有的問題作過綜述.上面所述的8個方面的問題，有的已經徹底解決，有的尚有遺留的情況待解決，并且，一些已經得到的結論仍然可以優化.

在比較久遠的古代，二次方程的求根公式就已經被埃及和巴比倫的先民們發現并記載，本文所列的第一篇文章，就是從實系數二次方程的實根的三種情況作類比而得到的，這種類比一直貫穿到F上的二次方程的研究之中.對有的讀者而言，通過閱讀二次方程的研究歷程，能夠得到一些數學科研的啟發乃至訓練.

在16世紀的一段時間里，尋找三次方程的求根公式成為意大利數學家們的熱門問題，并流傳下來一些動人的故事，求根公式終于被找到，從而促使人們向著四次和更高次的方程挺進，促進了代數學的發展，奠定了近代數學產生的直接基礎.上文中的式子，不僅是求根公式的重要組成部分，而且是討論實系數三次方程的實根狀況的直接依據，當然，它在本文中也起了很大的作用，從而對于讀者同樣具有啟發意義.

該文最后列出了44篇有關的參考文獻，而筆者獨立完成的有34篇，其中，被美國Math.Riews評述5篇，另列入索引2篇，說明有的論文具有一定的學術水平.長時間(30年)以來，該文所述的若干問題是筆者最先提出并發表研究結果的，從而引起有的代數學同行的關注和參與，因此，成為筆者的代數學研究的主要方向之一.

［1］孫宗明.質數模的二次同余式的根的狀況［J］.曲阜師范學報(自然科學版)，1981，(2):43－44.

［2］孫宗明.pk(p≥3)元域上的二次方程的根的狀況［J］.數學的實踐與認識，1983，(4):29－31(美國，Math.Riews，85i:11104).

［3］唐俊杰.有限域GF(2m)上的二次方程根的判別［J］.數學的實踐與認識，1986，(2):57－59.

［4］宋雪清.pk(p＞3)元域上的三次方程［J］.數學的實踐與認識，1986，(4):33－38.

［5］李慶.關于pk(p＞3)元域上的三次方程的一個注記［J］.數學的實踐與認識，1990，(2):75－77.

［6］孫宗明.2k元域上的三次方程根的狀況［J］.內蒙古師大學報(自然科學漢文版)，1993，(2):21－26(美國，Math.Riews，96c: 12003).

［7］孫宗明.關于pk(p＞3)元域上的三次方程［J］.泰安師專學報，2001，(3):1－6.

［8］孫宗明，等.3k元域上的三次方程根的簡況［J］.廣西師范學院學報(自然科學版)，1995，(2):32－34.

［9］孫宗明.pk元域上的三次方程根的狀況［J］.內蒙古師大學報(自然科學漢文版)，2001，(3):28－31.

［10］熊全淹.近世代數［M］.上海:上海科學技術出版社，1978.

［11］孫宗明.pk元域F的單超越擴域E上的二次方程［J］.河北師范大學學報(自然科學版)，1992，(3):14－16.

［12］孫宗明.2k元域上的二次方程根的公式［J］.數學的實踐與認識，2001，(6):132－133(美國，Math.Riews，2002年索引).

［13］王念平.關于“2k元域上的二次方程根的公式”的注記［J］.數學的實踐與認識，2004，(11):148－152.

［14］孫宗明.pk元域F及F的單超越擴域E上的二項方程［J］.泰安師專學報，2001，(3):4－8.

［15］孫宗明.pk元域上的2pl次方程根的狀況［J］.數學的實踐與認識，1987，(1):43－45(美國，Math.Riews，1988年索引).

［16］孫宗明.pk元域上的方程xq=d與ax2q+bxq+c=0［J］.內蒙古師大學報(自然科學漢文版)，1990，(1):22－26(美國，Math.Riews，92h:11110).

［17］孫宗明.pk元域上的二項方程和三項方程根的狀況［J］.內蒙古師大學報(自然科學漢文版)，1991，(3):20－24(美國，Math.Riews，96f:12001).

［18］孫宗明.pk元域F的單超越擴域E上的方程yn=D與Ay2n+Byn+C=0［J］.內蒙古師大學報(自然科學漢文版)，2000，(3):9－12.

［19］孫宗明.pk元域上的一類方程根的狀況［J］.河北師范大學學報(自然科學版)，1996，(2):23－25.

［20］孫宗明.pk(p≥3)元域上的方程∑(－1)iaixn－1－i=0［J］.岱宗學刊(自然科學版)，1999，(2):20－23.

［21］孫宗明.2k元域上的方程∑(－1)iaixn－1－i=0［J］.山東科技大學學報(自然科學版)，2001，(1):10－12(美國，Math.Riews，2002b:11172).

［22］孫宗明.pk元域上的方程∑k－10aixn－1－i=0［J］.廣西師范學院學報(自然科學版)，2003，(4):29－31.

［23］孫宗明.pk元域上的方程∑aixn－1－i=0與∑(－a)ixn－1－i=0［J］.商丘師范學院學報，2005，(2):57－59.

［24］孫宗明.pk元域F的單超越擴域E上的方程∑Aixn－1－i=0與∑(－A)ixn－1－i=0［J］.集美大學學報(自然科學版)，2007，(2):129－132.

［25］孫宗明.p2m元域上的某些方程的解的狀況［J］.吉安師專自然科學學報，1986，(2):34－36.

［26］孫宗明，等.pk元域上的方程xq+1=λ與x+xq=μ［J］.山東師大學報(自然科學版)，1994，(2):11－13.

［27］孫宗明.p元域上的一類不可約多項［J］.殷都學刊(自然科學版)，1990，(1):22－23.

［28］孫宗明.pk元域上的方程xps－x－c=0［J］.周口師范學院學報，2011，(5).

［29］孫宗明.有限循環群的若干特征性質［J］.曲阜師院學報(自然科學版)，1982，(3):50－54.

［30］孫宗明.pk元域中元素的n次根［J］.周口師范學院學報，2011，(2):8－11.

［31］孫宗明.線性矩陣方程(組)的理論［J］.益陽師專學報，1993，(6):25－30(美國，Math.Riews，1994年索引).

［32］孫宗明.pk元域上線性矩陣方程(組)的理論［J］.周口師范學院學報，2008，(2):19－20，26.

［33］孫宗明.有限域上二項方程根的求法［J］.山東教育學院學報，1989，(4):36－39.

［34］孫宗明.pk元域上一元方程的幾個降次定理［J］.山東教育學院學報，1991，(2):31－33.

［35］孫宗明.有限域上的不可約多項式的存在性與求法［J］.開封大學學報，1993，(3):16－19.

［36］孫宗明.域Fp與Fq上的m次不可約多項式［J］.殷都學刊(自然科學版)，1993，(4):38－41.

［37］孫宗明.有限域上的不可約多項式的根號解［J］.內蒙古師大學報(自然科學漢文版)，1995，(2):12－15.

［38］孫宗明，等.pk元域上的n方元素［J］.廣西師范學院學報(自然科學版)，1995(增刊):6－8.

［39］孫宗明.Fp［x］中的本原多項式與GF(Pn)中的本原元素［J］.泰安師專學報(自然科學版)，1990，(2):1－5.

［40］孫宗明.pk元域的m次不可約多項式與xpkm－x的因式分解［J］.泰安師專學報(自然科學版)，1995，(2):9－12.

［41］孫宗明，等.關于pk元域上的二項方程［J］.泰安師專學報(自然科學版)，1994，(2):17－21.

［42］孫宗明.pk(p＞3)元域上的三次方程根的狀況［J］.長沙大學學報，2000，(4):13－17，21.

［43］孫宗明.pk元域F及其單超越擴域E上的四類方程［J］.長沙大學學報，2003，(1):23－27.

［44］孫宗明.pk元域上的二次方程根的判定［J］.泰山學院學報，2010，(3):8－14.